大话数据结构C语言60 B树

Posted 2021-05-23 是CodeAllen

欢迎关注我的公众号是【CodeAllen】，关注回复【1024】获取精品学习资源
程序员技术交流①群：736386324 
程序员技术交流②群：371394777    

B树（B-tree）是一种平衡的多路查找树，2-3树和2-3-4树就是B树的特例

结点最大的孩子数目称为B树的阶（order），因此，2-3树是3阶B树，2-3-4树是4阶B树

 

一个m阶的B树具有如下属性：

1.如果根结点不是叶结点，则其至少有两棵子树

2.每一个非根的分支结点都有k-1个元素（关键字）和k个孩子，其中k满足：⌈m/2⌉ <= k <= m

3.所有叶子结点都位于同一层次

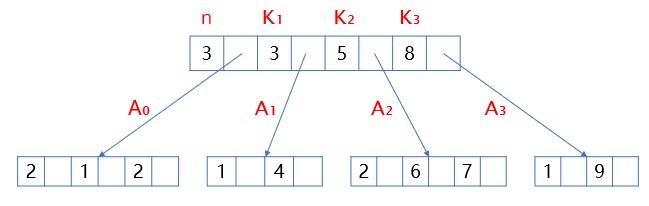
4.每一个分支结点包含下列信息数据：

n, A₀, K₁, A₁, K₂, A₂, K₃, A₃……

其中K为关键字，且Ki < Ki+1

Ai为指向子树根结点的指针

 

 

c文件

//代码来自（该文章有细致讲解）：http://blog.csdn.net/v_july_v/article/details/6735293
//实现对order序(阶)的B-TREE结构基本操作的封装。  
//查找：search，插入：insert，删除：remove。  
//创建：create，销毁：destory，打印：print。  
#include <stdlib.h>  
#include <stdio.h>  
#include <assert.h>  
#include "btree.h"  
  
//#define max(a, b) (((a) > (b)) ? (a) : (b))  
#define cmp(a, b) ( ( ((a)-(b)) >= (0) ) ? (1) : (0) ) //比较a，b大小  
#define DEBUG_BTREE  
  
  
// 模拟向磁盘写入节点  
void disk_write(BTNode* node)  
{  
//打印出结点中的全部元素，方便调试查看keynum之后的元素是否为0(即是否存在垃圾数据)；而不是keynum个元素。  
    printf("向磁盘写入节点");  
    for(int i=0;i<ORDER-1;i++){  
        printf("%c",node->key[i]);  
    }  
    printf("\\n");  
}  
  
// 模拟从磁盘读取节点  
void disk_read(BTNode** node)  
{  
//打印出结点中的全部元素，方便调试查看keynum之后的元素是否为0(即是否存在垃圾数据)；而不是keynum个元素。  
    printf("向磁盘读取节点");  
    for(int i=0;i<ORDER-1;i++){  
        printf("%c",(*node)->key[i]);  
    }  
    printf("\\n");  
}  
  
// 按层次打印 B 树  
void BTree_print(const BTree tree, int layer)  
{  
    int i;  
    BTNode* node = tree;  
  
    if (node) {  
        printf("第 %d 层， %d node : ", layer, node->keynum);  
  
        //打印出结点中的全部元素，方便调试查看keynum之后的元素是否为0(即是否存在垃圾数据)；而不是keynum个元素。  
        for (i = 0; i < ORDER-1; ++i) {  
        //for (i = 0; i < node->keynum; ++i) {  
            printf("%c ", node->key[i]);  
        }  
  
        printf("\\n");  
  
        ++layer;  
        for (i = 0 ; i <= node->keynum; i++) {  
            if (node->child[i]) {  
                BTree_print(node->child[i], layer);  
            }  
        }  
    }  
    else {  
        printf("树为空。\\n");  
    }  
}  
  
// 结点node内对关键字进行二分查找。  
int binarySearch(BTNode* node, int low, int high, KeyType Fkey)  
{  
    int mid;  
    while (low<=high)  
    {  
        mid = low + (high-low)/2;  
        if (Fkey<node->key[mid])  
        {  
            high = mid-1;  
        }  
        if (Fkey>node->key[mid])  
        {  
            low = mid+1;  
        }  
        if (Fkey==node->key[mid])  
        {  
            return mid;//返回下标。  
        }  
    }  
    return 0;//未找到返回0.  
}  
  
//insert  
/*************************************************************************************** 
   将分裂的结点中的一半元素给新建的结点，并且将分裂结点中的中间关键字元素上移至父节点中。 
   parent 是一个非满的父节点 
   node 是 tree 孩子表中下标为 index 的孩子节点，且是满的，需分裂。 
*******************************************************************/  
void BTree_split_child(BTNode* parent, int index, BTNode* node)  
{  
#ifdef DEBUG_BTREE  
    printf("BTree_split_child!\\n");  
#endif  
    assert(parent && node);  
    int i;  
  
    // 创建新节点，存储 node 中后半部分的数据  
    BTNode* newNode = (BTNode*)calloc(sizeof(BTNode), 1);  
    if (!newNode) {  
        printf("Error! out of memory!\\n");  
        return;  
    }  
  
    newNode->isLeaf = node->isLeaf;  
    newNode->keynum = BTree_D - 1;  
  
    // 拷贝 node 后半部分关键字,然后将node后半部分置为0。  
    for (i = 0; i < newNode->keynum; ++i){  
        newNode->key[i] = node->key[BTree_D + i];  
        node->key[BTree_D + i] = 0;  
    }  
  
    // 如果 node 不是叶子节点，拷贝 node 后半部分的指向孩子节点的指针，然后将node后半部分指向孩子节点的指针置为NULL。  
    if (!node->isLeaf) {  
        for (i = 0; i < BTree_D; i++) {  
            newNode->child[i] = node->child[BTree_D + i];  
            node->child[BTree_D + i] = NULL;  
        }  
    }  
  
    // 将 node 分裂出 newNode 之后，里面的数据减半  
    node->keynum = BTree_D - 1;  
  
    // 调整父节点中的指向孩子的指针和关键字元素。分裂时父节点增加指向孩子的指针和关键元素。  
    for (i = parent->keynum; i > index; --i) {  
        parent->child[i + 1] = parent->child[i];  
    }  
  
    parent->child[index + 1] = newNode;  
  
    for (i = parent->keynum - 1; i >= index; --i) {  
        parent->key[i + 1] = parent->key[i];  
    }  
  
    parent->key[index] = node->key[BTree_D - 1];  
    ++parent->keynum;  
  
    node->key[BTree_D - 1] = 0;  
  
    // 写入磁盘  
     disk_write(parent);  
     disk_write(newNode);  
     disk_write(node);  
}  
  
void BTree_insert_nonfull(BTNode* node, KeyType key)  
{  
    assert(node);  
  
    int i;  
  
    // 节点是叶子节点，直接插入  
    if (node->isLeaf) {  
        i = node->keynum - 1;  
        while (i >= 0 && key < node->key[i]) {  
            node->key[i + 1] = node->key[i];  
            --i;  
        }  
  
        node->key[i + 1] = key;  
        ++node->keynum;  
  
        // 写入磁盘  
        disk_write(node);  
    }  
  
    // 节点是内部节点  
    else {  
        /* 查找插入的位置*/  
        i = node->keynum - 1;  
        while (i >= 0 && key < node->key[i]) {  
            --i;  
        }  
  
        ++i;  
  
        // 从磁盘读取孩子节点  
        disk_read(&node->child[i]);  
  
        // 如果该孩子节点已满，分裂调整值  
        if (node->child[i]->keynum == (ORDER-1)) {  
            BTree_split_child(node, i, node->child[i]);  
            // 如果待插入的关键字大于该分裂结点中上移到父节点的关键字，在该关键字的右孩子结点中进行插入操作。  
            if (key > node->key[i]) {  
                ++i;  
            }  
        }  
        BTree_insert_nonfull(node->child[i], key);  
    }  
}  
  
void BTree_insert(BTree* tree, KeyType key)  
{  
#ifdef DEBUG_BTREE  
    printf("BTree_insert:\\n");  
#endif  
    BTNode* node;  
    BTNode* root = *tree;  
  
    // 树为空  
    if (NULL == root) {  
        root = (BTNode*)calloc(sizeof(BTNode), 1);  
        if (!root) {  
            printf("Error! out of memory!\\n");  
            return;  
        }  
        root->isLeaf = true;  
        root->keynum = 1;  
        root->key[0] = key;  
  
        *tree = root;  
  
        // 写入磁盘  
        disk_write(root);  
  
        return;  
    }  
  
    // 根节点已满，插入前需要进行分裂调整  
    if (root->keynum == (ORDER-1)) {  
        // 产生新节点当作根  
        node = (BTNode*)calloc(sizeof(BTNode), 1);  
        if (!node) {  
            printf("Error! out of memory!\\n");  
            return;  
        }  
  
        *tree = node;  
        node->isLeaf = false;  
        node->keynum = 0;  
        node->child[0] = root;  
  
        BTree_split_child(node, 0, root);  
  
        BTree_insert_nonfull(node, key);  
    }  
  
    // 根节点未满，在当前节点中插入 key  
    else {  
        BTree_insert_nonfull(root, key);  
    }  
}  
//remove   
// 对 tree 中的节点 node 进行合并孩子节点处理.  
// 注意：孩子节点的 keynum 必须均已达到下限，即均等于 BTree_D - 1  
// 将 tree 中索引为 index 的 key 下移至左孩子结点中，  
// 将 node 中索引为 index + 1 的孩子节点合并到索引为 index 的孩子节点中，右孩子合并到左孩子结点中。  
// 并调相关的 key 和指针。</p>void BTree_merge_child(BTree* tree, BTNode* node, int index)  
{  
#ifdef DEBUG_BTREE  
    printf("BTree_merge_child!\\n");  
#endif  
    assert(tree && node && index >= 0 && index < node->keynum);  
  
    int i;  
  
    KeyType key = node->key[index];  
    BTNode* leftChild = node->child[index];  
    BTNode* rightChild = node->child[index + 1];  
  
    assert(leftChild && leftChild->keynum == BTree_D - 1  
        && rightChild && rightChild->keynum == BTree_D - 1);  
  
    // 将 node中关键字下标为index 的 key 下移至左孩子结点中，该key所对应的右孩子结点指向node的右孩子结点中的第一个孩子。  
    leftChild->key[leftChild->keynum] = key;  
    leftChild->child[leftChild->keynum + 1] = rightChild->child[0];  
    ++leftChild->keynum;  
  
    // 右孩子的元素合并到左孩子结点中。  
    for (i = 0; i < rightChild->keynum; ++i) {  
        leftChild->key[leftChild->keynum] = rightChild->key[i];  
        leftChild->child[leftChild->keynum + 1] = rightChild->child[i + 1];  
        ++leftChild->keynum;  
    }  
  
    // 在 node 中下移的 key后面的元素前移  
    for (i = index; i < node->keynum - 1; ++i) {  
        node->key[i] = node->key[i + 1];  
        node->child[i + 1] = node->child[i + 2];  
    }  
    node->key[node->keynum - 1] = 0;  
    node->child[node->keynum] = NULL;  
    --node->keynum;  
  
    // 如果根节点没有 key 了，并将根节点调整为合并后的左孩子节点；然后删除释放空间。  
    if (node->keynum == 0) {  
        if (*tree == node) {  
            *tree = leftChild;  
        }  
  
        free(node);  
        node = NULL;  
    }  
  
    free(rightChild);  
    rightChild = NULL;  
}  
  
void BTree_recursive_remove(BTree* tree, KeyType key)  
{  
    // B-数的保持条件之一：  
    // 非根节点的内部节点的关键字数目不能少于 BTree_D - 1  
  
    int i, j, index;  
    BTNode *root = *tree;  
    BTNode *node = root;  
  
    if (!root) {  
        printf("Failed to remove %c, it is not in the tree!\\n", key);  
        return;  
    }  
  
    // 结点中找key。  
    index = 0;  
    while (index < node->keynum && key > node->key[index]) {  
        ++index;  
    }  
  
/*======================含有key的当前结点时的情况==================== 
node: 
index of Key:            i-1  i  i+1 
                        +---+---+---+---+ 
                          *  key   * 
                    +---+---+---+---+---+ 
                           /     \\ 
index of Child:           i      i+1 
                         /         \\ 
                    +---+---+      +---+---+ 
                      *   *           *   *    
                +---+---+---+  +---+---+---+ 
                    leftChild     rightChild 
============================================================*/  
    /*一、结点中找到了关键字key的情况.*/  
    BTNode *leftChild, *rightChild;  
    KeyType leftKey, rightKey;  
    if (index < node->keynum && node->key[index] == key) {  
        /* 1，所在节点是叶子节点，直接删除*/  
        if (node->isLeaf) {  
            for (i = index; i < node->keynum-1; ++i) {  
                node->key[i] = node->key[i + 1];  
                //node->child[i + 1] = node->child[i + 2];叶子节点的孩子结点为空，无需移动处理。  
            }  
            node->key[node->keynum-1] = 0;  
            //node->child[node->keynum] = NULL;  
            --node->keynum;  
  
            if (node->keynum == 0) {  
                assert(node == *tree);  
                free(node);  
                *tree = NULL;  
            }  
  
            return;  
        }  
        /*2.选择脱贫致富的孩子结点。*/  
        // 2a，选择相对富有的左孩子结点。  
        // 如果位于 key 前的左孩子结点的 key 数目 >= BTree_D，  
        // 在其中找 key 的左孩子结点的最后一个元素上移至父节点key的位置。  
        // 然后在左孩子节点中递归删除元素leftKey。  
        else if (node->child[index]->keynum >= BTree_D) {  
            leftChild = node->child[index];  
            leftKey = leftChild->key[leftChild->keynum - 1];  
            node->key[index] = leftKey;  
  
            BTree_recursive_remove(&leftChild, leftKey);  
        }  
        // 2b，选择相对富有的右孩子结点。  
        // 如果位于 key 后的右孩子结点的 key 数目 >= BTree_D，  
        // 在其中找 key 的右孩子结点的第一个元素上移至父节点key的位置  
        // 然后在右孩子节点中递归删除元素rightKey。  
        else if (node->child[index + 1]->keynum >= BTree_D) {  
            rightChild = node->child[index + 1];  
            rightKey = rightChild->key[0];  
            node->key[index] = rightKey;  
  
            BTree_recursive_remove(&rightChild, rightKey);  
        }  
        /*左右孩子结点都刚脱贫。删除前需要孩子结点的合并操作*/  
        // 2c，左右孩子结点只包含 BTree_D - 1 个节点，  
        // 合并是将 key 下移至左孩子节点，并将右孩子节点合并到左孩子节点中，  
        // 删除右孩子节点，在父节点node中移除 key 和指向右孩子节点的指针，  
        // 然后在合并了的左孩子节点中递归删除元素key。  
        else if (node->child[index]->keynum == BTree_D - 1  
            && node->child[index + 1]->keynum == BTree_D - 1){  
            leftChild = node->child[index];  
  
            BTree_merge_child(tree, node, index);  
  
            // 在合并了的左孩子节点中递归删除 key  
            BTree_recursive_remove(&leftChild, key);  
        }  
    }  
  
/*======================未含有key的当前结点时的情况==================== 
node: 
index of Key:            i-1  i  i+1 
                        +---+---+---+---+ 
                          *  keyi * 
                    +---+---+---+---+---+ 
                       /    |    \\ 
index of Child:      i-1    i     i+1 
                     /      |       \\ 
            +---+---+   +---+---+      +---+---+ 
             *   *        *   *          *   *    
        +---+---+---+   +---+---+---+  +---+---+---+ 
        leftSibling       Child        rightSibling  
============================================================*/  
    /*二、结点中未找到了关键字key的情况.*/  
    else {  
        BTNode *leftSibling, *rightSibling, *child;  
        // 3. key 不在内节点 node 中，则应当在某个包含 key 的子节点中。  
        //  key < node->key[index], 所以 key 应当在孩子节点 node->child[index] 中  
        child = node->child[index];  
        if (!child) {  
            printf("Failed to remove %c, it is not in the tree!\\n", key);  
            return;  
        }  
        /*所需查找的该孩子结点刚脱贫的情况*/  
        if (child->keynum == BTree_D - 1) {  
            leftSibling = NULL;  
            rightSibling = NULL;  
  
            if (index - 1 >= 0) {  
                leftSibling = node->child[index - 1];  
            }  
  
            if (index + 1 <= node->keynum) {  
                rightSibling = node->child[index + 1];  
            }  
            /*选择致富的相邻兄弟结点。*/  
            // 3a，如果所在孩子节点相邻的兄弟节点中有节点至少包含 BTree_D 个关键字  
            // 将 node 的一个关键字key[index]下移到 child 中，将相对富有的相邻兄弟节点中一个关键字上移到  
            // node 中，然后在 child 孩子节点中递归删除 key。  
            if ((leftSibling && leftSibling->keynum >= BTree_D)  
                || (rightSibling && rightSibling->keynum >= BTree_D)) {  
                int richR = 0;  
                if(rightSibling) richR = 1;  
                if(leftSibling && rightSibling) {  
                    richR = cmp(rightSibling->keynum,leftSibling->keynum);  
                }  
                if (rightSibling && rightSibling->keynum >= BTree_D && richR) {  
        //相邻右兄弟相对富有，则该孩子先向父节点借一个元素，右兄弟中的第一个元素上移至父节点所借位置，并进行相应调整。  
                    child->key[child->keynum] = node->key[index];  
                    child->child[child->keynum + 1] = rightSibling->child[0];  
                    ++child->keynum;  
  
                    node->key[index] = rightSibling->key[0];  
  
                    for (j = 0; j < rightSibling->keynum - 1; ++j) {//元素前移  
                        rightSibling->key[j] = rightSibling->key[j + 1];  
                        rightSibling->child[j] = rightSibling->child[j + 1];  
                    }  
                    rightSibling->key[rightSibling->keynum-1] = 0;  
                    rightSibling->child[rightSibling->keynum-1] = rightSibling->child[rightSibling->keynum];  
                    rightSibling->child[rightSibling->keynum] = NULL;  
                    --rightSibling->keynum;  
                }  
                else {//相邻左兄弟相对富有，则该孩子向父节点借一个元素，左兄弟中的最后元素上移至父节点所借位置，并进行相应调整。  
                    for (j = child->keynum; j > 0; --j) {//元素后移  
                        child->key[j] = child->key[j - 1];  
                        child->child[j + 1] = child->child[j];  
                    }  
                    child->child[1] = child->child[0];  
                    child->child[0] = leftSibling->child[leftSibling->keynum];  
                    child->key[0] = node->key[index - 1];  
                    ++child->keynum;  
  
                    node->key[index - 1] = leftSibling->key[leftSibling->keynum - 1];  
  
                    leftSibling->key[leftSibling->keynum - 1] = 0;  
                    leftSibling->child[leftSibling->keynum] = NULL;  
  
                    --leftSibling->keynum;  
                }  
            }  
            /*相邻兄弟结点都刚脱贫。删除前需要兄弟结点的合并操作,*/  
            // 3b, 如果所在孩子节点相邻的兄弟节点都只包含 BTree_D - 1 个关键字，  
            // 将 child 与其一相邻节点合并，并将 node 中的一个关键字下降到合并节点中，  
            // 再在 node 中删除那个关键字和相关指针，若 node 的 key 为空，删之，并调整根为合并结点。  
            // 最后，在相关孩子节点child中递归删除 key。  
            else if ((!leftSibling || (leftSibling && leftSibling->keynum == BTree_D - 1))  
                && (!rightSibling || (rightSibling && rightSibling->keynum == BTree_D - 1))) {  
                if (leftSibling && leftSibling->keynum == BTree_D - 1) {  
  
                    BTree_merge_child(tree, node, index - 1);//node中的右孩子元素合并到左孩子中。  
  
                    child = leftSibling;  
                }  
  
                else if (rightSibling && rightSibling->keynum == BTree_D - 1) {  
  
                    BTree_merge_child(tree, node, index);//node中的右孩子元素合并到左孩子中。  
                }  
            }  
        }  
  
        BTree_recursive_remove(&child, key);//调整后，在key所在孩子结点中继续递归删除key。  
    }  
}  
  
void BTree_remove(BTree* tree, KeyType key)  
{  
#ifdef DEBUG_BTREE  
    printf("BTree_remove:\\n");  
#endif  
    if (*tree==NULL)  
    {     
        printf("BTree is NULL!\\n");  
        return;  
    }  
  
    BTree_recursive_remove(tree, key);  
}  
  
//=====================================search====================================  
  
BTNode* BTree_recursive_search(const BTree tree, KeyType key, int* pos)  
{  
    int i = 0;  
  
    while (i < tree->keynum && key > tree->key[i]) {  
        ++i;  
    }  
  
    // Find the key.  
    if (i < tree->keynum && tree->key[i] == key) {  
        *pos = i;  
        return tree;  
    }  
  
    // tree 为叶子节点，找不到 key，查找失败返回  
    if (tree->isLeaf) {  
        return NULL;  
    }  
  
    // 节点内查找失败，但 tree->key[i - 1]< key < tree->key[i]，  
    // 下一个查找的结点应为 child[i]  
  
    // 从磁盘读取第 i 个孩子的数据  
    disk_read(&tree->child[i]);  
  
    // 递归地继续查找于树 tree->child[i]  
    return BTree_recursive_search(tree->child[i], key, pos);  
}  
  
BTNode* BTree_search(const BTree tree, KeyType key, int* pos)  
{  
#ifdef DEBUG_BTREE  
    printf("BTree_search:\\n");  
#endif  
    if (!tree) {  
        printf("BTree is NULL!\\n");  
        return NULL;  
    }  
    *pos = -1;  
    return BTree_recursive_search(tree,key,pos);  
}  
  
//===============================create===============================  
void BTree_create(BTree* tree, const KeyType* data, int length)  
{  
    assert(tree);  
  
    int i;  
  
#ifdef DEBUG_BTREE  
    printf("\\n 开始创建 B-树，关键字为:\\n");  
    for (i = 0; i < length; i++) {  
        printf(" %c ", data[i]);  
    }  
    printf("\\n");  
#endif  
  
    for (i = 0; i < length; i++) {  
#ifdef DEBUG_BTREE  
        printf("\\n插入关键字 %c:\\n", data[i]);  
#endif  
        int pos = -1;  
        BTree_search(*tree,data[i],&pos);//树的递归搜索。  
        if (pos!=-1)  
        {  
            printf("this key %c is in the B-tree,not to insert.\\n",data[i]);  
        }else{  
            BTree_insert(tree, data[i]);//插入元素到BTree中。  
        }  
  
#ifdef DEBUG_BTREE  
        BTree_print(*tree);//树的深度遍历。  
#endif  
    }  
  
    printf("\\n");  
}  
//===============================destroy===============================  
void BTree_destroy(BTree* tree)  
{  
    int i;  
    BTNode* node = *tree;  
  
    if (node) {  
        for (i = 0; i <= node->keynum; i++) {  
            BTree_destroy(&node->child[i]);  
        }  
  
        free(node);  
    }  
  
    *tree = NULL;  
}  

头文件

//实现对order序(阶)的B-TREE结构基本操作的封装。  
//查找：search，插入：insert，删除：remove。  
//创建：create，销毁：destory，打印：print。  
#ifndef BTREE_H  
#define BTREE_H  
  
#ifdef __cplusplus  
extern "C" {  
#endif  
  
* 定义m序(阶)B 树的最小度数BTree_D=ceil(m)*/  
/// 在这里定义每个节点中关键字的最大数目为:2 * BTree_D - 1，即序(阶)：2 * BTree_D.  
#define BTree_D        2  
#define ORDER        (BTree_D * 2) //定义为4阶B-tree,2-3-4树。最简单为3阶B-tree,2-3树。  
//#define ORDER        (BTree_T * 2-1)  //最简单为3阶B-tree,2-3树。  
  
    typedef int KeyType;  
    typedef struct BTNode{  
        int keynum;                        /// 结点中关键字的个数，keynum <= BTree_N  
        KeyType key[ORDER-1];                /// 关键字向量为key[0..keynum - 1]  
        struct BTNode* child[ORDER];        /// 孩子指针向量为child[0..keynum]  
        bool isLeaf;                    /// 是否是叶子节点的标志  
    }BTNode;  
      
    typedef BTNode* BTree;  ///定义BTree  
      
    ///给定数据集data,创建BTree。  
    void BTree_create(BTree* tree, const KeyType* data, int length);  
  
    ///销毁BTree，释放内存空间。  
    void BTree_destroy(BTree* tree);  
      
    ///在BTree中插入关键字key。  
    void BTree_insert(BTree* tree, KeyType key);  
  
    ///在BTree中移除关键字key。  
    void BTree_remove(BTree* tree, KeyType key);  
  
    ///深度遍历BTree打印各层结点信息。  
    void BTree_print(const BTree tree, int layer=1);  
      
    /// 在BTree中查找关键字 key，  
    /// 成功时返回找到的节点的地址及 key 在其中的位置 *pos  
    /// 失败时返回 NULL 及查找失败时扫描到的节点位置 *pos  
    BTNode* BTree_search(const BTree tree, int key, int* pos);  
      
#ifdef __cplusplus  
}  
#endif  
  
#endif