强交变磁场下的AD转换数值的变化
Posted 卓晴
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了强交变磁场下的AD转换数值的变化相关的知识,希望对你有一定的参考价值。

简 介: 针对无线充电线圈内强磁场的干扰引起单片机电路中测量信号的变化,讨论了产生这种变化的背后的机理。给出了在强信号、高频信号下对于电路设计中的EMC的要求以及想预定的处理方法。
关键词: EMC,非线性,屏幕,高频干扰
§01 为什么AD数值会变化?
大大,我是信标组的。当超级电容给主板供电,用tc264的ad口检测电容电压值。我用100k和10k的电阻分压检测,检测到的值比实际值衰减11倍。把车放在灯上,在没有发射150khz信号时,检测压值是正确的,但是当发射150khz信号时,检测到的电压值会突然上升,比如从0.5直接升到1.3。我在一些群里问了,部分人也有遇到过这个问题,这是为什么呢?
在下面是无线电能接收板上的基本结构。其中也包括有对于输出电能进行检测的电阻分压接口。
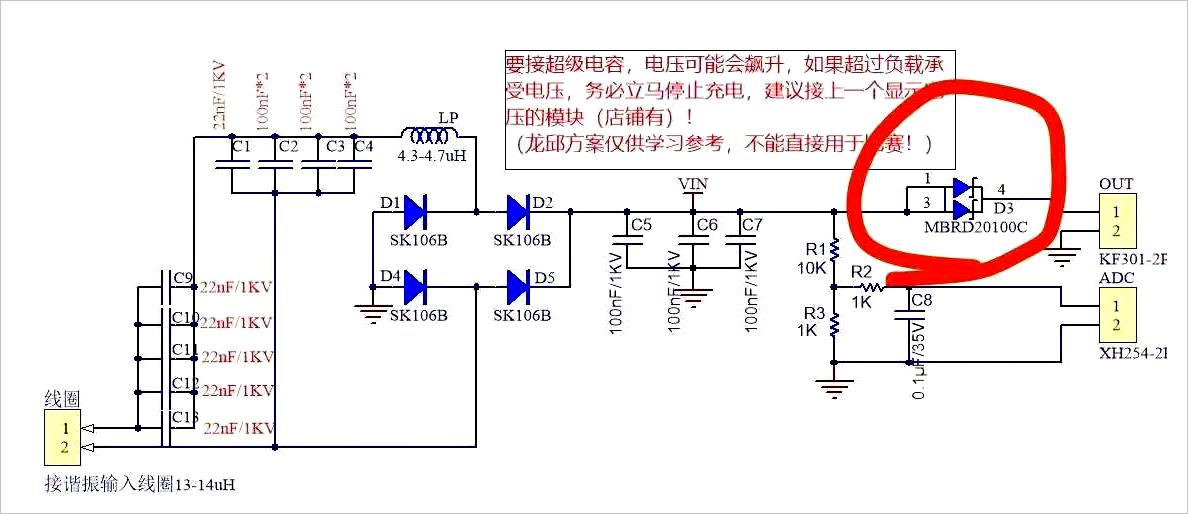
▲ 购买到的接受板LCC的电路原理图
§02 原因解释
回复: 在高频外部磁场干扰下,这其中的主要原因还是由于很强的交变磁场在电路板的引线上产生了很大的高频感应电动势,特别是AD输入模拟信号线上的高频感应电动势。它们会在电路中的一些非线性环节下,转换成直流电压,进而引起AD转换数值的变化。这说明在你的电路设计中在 电磁兼容性(EMC,即Electromagnetic Compatibility) 设计方面存在缺陷。
可以从以下三个方面进一步讨论:
1. 为什么非线性环节会从交流信号中产生直流信号?
2. 电子线路中通常存在哪些非线性环节?
3. 如何避免电路受到外部高频信号干扰?
1、非线性环节
如果测量信号上叠加有高频电动势,就像下面公式所示:
f ( t ) = s ( t ) + a ⋅ sin ( Ω t ) f\\left( t \\right) = s\\left( t \\right) + a \\cdot \\sin \\left( {\\Omega t} \\right) f(t)=s(t)+a⋅sin(Ωt)
-
其中参数:
-
s(t):实际信号
a·sin(Ωt):干扰高频信号
f(t):测量信号
对于AD转换数值来接可能只是在测量结果上出现上下波动,而不是AD转换至增大或者减小。比如在下面动图中显示的ESP32-S模块的采集ADC转换结果曲线。当无线充电线圈放在测量电路上方的时候,输出的结果表现为剧烈的上下跳动。
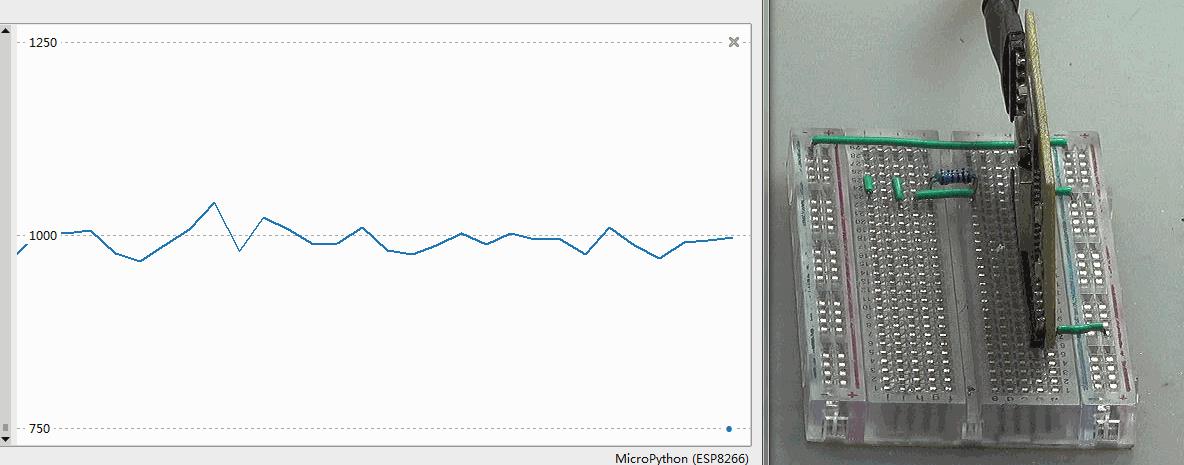
▲ 发射线圈对于AD转换的影响
那么为什么经过电路中非线性环节会出现附加的直流分量呢?
假设系统的非线性环节使用函数 H ( x ) H\\left( x \\right) H(x)表示,它代表将信号量 x x x转换成 H ( x ) H\\left( x \\right) H(x)。假设它在工作点 x 0 x_0 x0处具有任意阶导数,在 x 0 x_0 x0处进行台 劳级数(Taylor series) 展开: H ( x ) = H ( x 0 ) + H ′ ( x 0 ) ( x − x 0 ) + H ′ ′ ( x 0 ) 2 ! ( x − x 0 ) 2 + ⋯ H\\left( x \\right) = H\\left( {x_0 } \\right) + H'\\left( {x_0 } \\right)\\left( {x - x_0 } \\right) + {{H''\\left( {x_0 } \\right)} \\over {2!}}\\left( {x - x_0 } \\right)^2 + \\cdots H(x)=H(x0)+H′(x0)(x−x0)+2!H′′(x0)(x−x0)2+⋯
在其中的平方项中,就会产生如下分解:
( x − x 0 ) 2 = [ s ( t ) + a ⋅ sin ( Ω t ) − x 0 ] 2 \\left( {x - x_0 } \\right)^2 = \\left[ {s\\left( t \\right) + a \\cdot \\sin \\left( {\\Omega t} \\right) - x_0 } \\right]^2 (x−x0)2=[s(t)+a⋅sin(Ωt)−x0]2 = s 2 ( t ) + 2 s ( t ) ⋅ [ a ⋅ sin ( Ω t ) − x 0 ] + [ a ⋅ sin ( Ω t ) ] 2 − 2 a sin ( Ω t ) x 0 + x 0 2 = s^2 \\left( t \\right) + 2s\\left( t \\right) \\cdot \\left[ {a \\cdot \\sin \\left( {\\Omega t} \\right) - x_0 } \\right] + \\left[ {a \\cdot \\sin \\left( {\\Omega t} \\right)} \\right]^2 - 2a\\sin \\left( {\\Omega t} \\right)x_0 + x_0^2 =s2(t)+2s(t)⋅[a⋅sin(Ωt)−x0]+[a⋅sin(Ωt)]2−2asin(Ωt)x0+x02
其中关于叠加高频噪声的平方项中 [ a ⋅ sin ( Ω t ) ] 2 = a 2 [ 1 − cos ( 2 Ω t ) ] \\left[ {a \\cdot \\sin \\left( {\\Omega t} \\right)} \\right]^2 = {a \\over 2}\\left[ {1 - \\cos \\left( {2\\Omega t} \\right)} \\right] [a⋅sin(Ωt)]2=2a[1−cos(2Ωt)]
就会出现常数项 a / 2 a/2 a/2,这就是由于测量信号中交流信号经过非线性环节所产生的直流信号。
利用二极管对于交流信号进行整流形成直流信号也是利用的二极管单向导通的非线性。
2、电路中的非线性环节
在半导体电路线路中会存在很多非线性环节。比如在单片的IO端口通常会具有保护钳位二极管,防止输出信号超出允许电压范围。这就会对输入信号产生非线性作用。
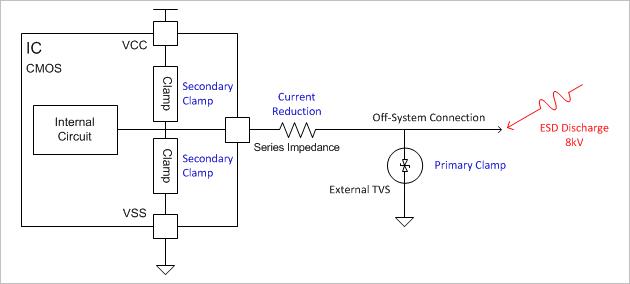
▲ 单片机端口中的钳位二极管
特别是当信号频率很高时,原来经过电路反馈呈现非常好的线性电路也会出现严重的非线性特性。比如在 为什么使用LM386可以直接收听调频电台节目? 中就对LM386音频运放在高频信号下所产生的直流偏置影响进行了讨论。
经过上面简单讨论可以知道,强高频电磁场下的电路设计需要特别考虑电磁兼容性(EMC)方面的要求。

▲ 实验电路板
3、如何避免高频信号干扰
一方面可以从电路布线设计方面进行考虑,比如尽量缩短电路信号线长度,避免大的引线回路,通过铺底线减少供地干扰等。比如在 无线节能信标调试说明-2021-3-3 中就讨论了在无线充电线圈中的发光盘上的引线布置,使其能够抑制无线充电线圈强磁场对于HALL传感器的影响。
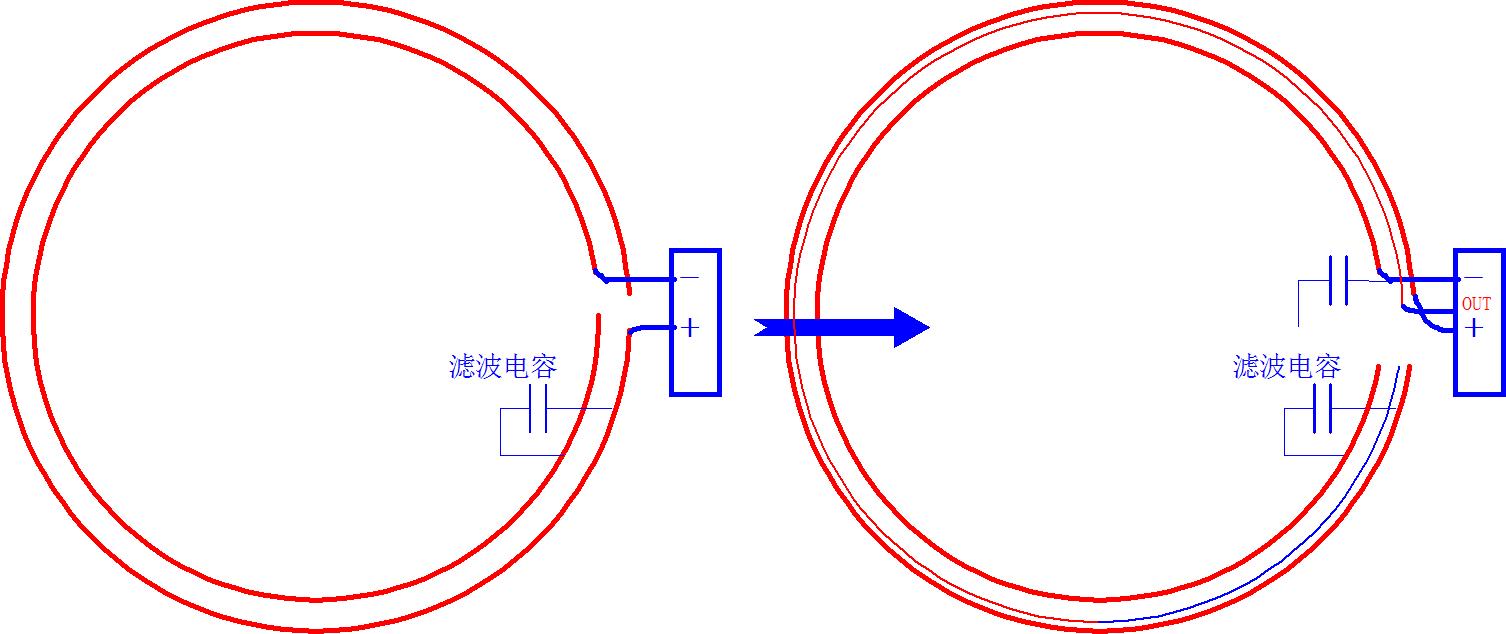
▲ 无线充电线圈中的发光盘线路布置
在线路敏感部分,比如模拟量采集电路,通过增加端口的低通滤波电路降低外部引线上感应干扰电压窜入电路。在MCU的ADC转换端口也增加相应的低通滤波电路降低信号的高频分量进入半导体器件。
此外,也可以考虑在物理上通过外部的磁屏蔽板来降低直接辐射的高频电磁场。比如在下面的节能车模车模中,在无线接收LCC网络电路中就是用了磁屏蔽板来消除高频强磁场对无线接收回路的影响。

▲ 用于减弱高频磁场干扰的磁屏蔽板
涉及到大功率、高频信号的时候,需要对电路设计加以额外的考虑,综合考虑信号的空间分布式耦合特性以及线路中可能存在的各种非线性的影响。
■ 相关文献链接:
以上是关于强交变磁场下的AD转换数值的变化的主要内容,如果未能解决你的问题,请参考以下文章