欠拟合和过拟合——机器学习

Posted 2021-05-21 神的孩子都在歌唱

欠拟合和过拟合

• • 一. 定义
  • 二 .过拟合
  • • 2.1 正则化——解决过拟合
    • • 2.1.1 定义
      • 2.1.2 正则化线性模型
    • 2.2 维灾难
  • 三. 波士顿房价预测讲解——岭回归
  • • • 3.1 API——Ridge
      • 3.2 API——RidgeCV
  • 三. 欠拟合

前言：

作者：神的孩子在跳舞
本人是刚开始学机器学习的小白，以下都是我的学习笔记，有一些是我自己理解的话，所以可能有不对的地方或者有些话只适合我自己理解（仅供参考），不对的希望大家能指出来，另外我创建了一个机器学习交流群903419026，各位跟我一样的小白可以进来多交流交流，互相促进，大佬看见了可以进来指导一下（狗头）。

通俗理解：通过判断一个高级物种是不是人类来进行解决的，通过学习有眼睛，有鼻子有嘴巴就是人类，结果出来一只猫我们也判断是人类，那么这就叫欠拟合，然后我们在训练，接下来在添加皮肤是黄色的就是人类，结果过来一个非洲大哥，判断为不是，这就是过拟合

一. 定义

1. 过拟合：一个假设在训练数据上能够获得比其他假设更好的拟合， 但是在测试数据集上却不能很好地拟合数据，此时认为这个假设出现了过拟合的现象。(模型过于复杂)
2. 欠拟合：一个假设在训练数据上不能获得更好的拟合，并且在测试数据集上也不能很好地拟合数据，此时认为这个假设出现了欠拟合的现象。(模型过于简单)

二 .过拟合

1. 效果：训练误差小，测试误差大

2. 原因：原始特征过多，存在一些嘈杂特征， 模型过于复杂是因为模型尝试去兼顾各个测试数据点

3. 解决：

   （1）重新清洗数据：导致过拟合的一个原因也有可能是数据不纯导致的，如果出现了过拟合就需要我们重新清洗数据。

   （2）增大数据的训练量：还有一个原因就是我们用于训练的数据量太小导致的，训练数据占总数据的比例过小。

   （3）正则化（接下来会详细解释）

   （4）减少特征维度，防止维灾难

2.1 正则化——解决过拟合

2.1.1 定义

1. 响应的进行限制

2. 有些样本需要训练，训练的过程中，进行拟合，有三种情况发生，直线（欠拟合），曲线，拐来拐去的线（过拟合）

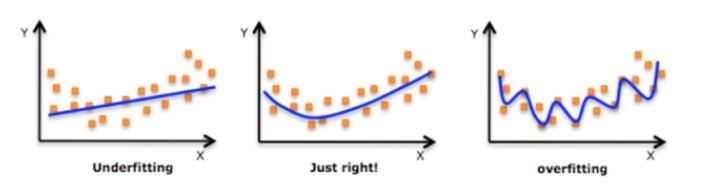
3. 过拟合变成曲线：尽量减小高次项特征的影响

4. 类别：
   （1）L1正则化（Lasso回归）：把高次项系数w的值变为0
   （2）L2正则化（岭回归）：把一些系数变得非常小

2.1.2 正则化线性模型

1. Ridge Regression (岭回归) 使用最多

1. 岭回归是线性回归的正则化版本，即在原来的线性回归的 cost function ( 所有样本误差的平均，也就是损失函数的平均 ) 中添加正则项（regularization term)
2. 放在均方误差里面
3. 思想：
   (1)就是把系数添加平方项
   (2)然后限制系数值的大小
   (3)α值越小，系数值越大，α越大，系数值越小

2. Lasso Regression(Lasso 回归)

1. Lasso Regression 有一个很重要的性质是：倾向于完全消除不重要的权重。

2. 对系数值进行绝对值处理：由于绝对值在顶点处不可导，所以进行计算的过程中产生很多0，最后得到结果为：稀疏矩阵

3. Elastic Net (弹性网络)

是前两个内容的综合:设置了一个r,如果r=0–岭回归；r=1–Lasso回归

2.2 维灾难

1. 定义：随着维度的增加，分类器性能逐步上升，到达某点之后，其性能便逐渐下降

2. 通俗理解：比如要判断一个对应的分类器，分类猫和狗，刚开始我们取一个特征，通过肤色划分，假设所有的花纹状的是猫，黄色的是狗。第二种特征，夏天舌头生出来的是狗，第三个叫声，随着特征增加（维度增多），很明显训练数据就很清楚，但是测试数据由于我们分的太细了就不能判断，容易发生过拟合，同时也是维灾难的体现

三. 波士顿房价预测讲解——岭回归

标准化：是对前面一些方法的封装，在使用线性回归，梯度下降，岭回归，我们会涉及到数据大小的计算，都需要特征工程里面的把数据变成到特定范围内（标准化），在进行值的变换

3.1 API——Ridge

sklearn.linear_model.Ridge(alpha=1.0, fit_intercept=True,solver="auto", normalize=False)

参数介绍

1. 具有l2正则化的线性回归
2. alpha:正则化力度，也叫 λ，通过这个力度来进行响应值的判断，值越大，正则化力度越大，相应的系数会越小，默认值是1
3. solver:会根据数据自动选择优化方法 sag:如果数据集、特征都比较大，选择该SAG随机梯度下降优化
4. normalize:默认进行标准化处理 normalize=False:可以在fit之前调用preprocessing.StandardScaler标准化数据
5. Ridge.coef_:回归权重
6. Ridge.intercept_:回归偏置

代码

from sklearn.datasets import load_boston#导入数据
from sklearn.model_selection import train_test_split#数据集划分
from sklearn.preprocessing import StandardScaler#特征工程标准化
from sklearn.linear_model import Ridge#岭回归
from sklearn.metrics import mean_squared_error#模型评估

boston=load_boston()
boston

#数据集划分
x_train, x_test, y_train, y_test = train_test_split(boston.data,boston.target,test_size=0.2)
x_train

transfer=StandardScaler()#实例化一个对象
x_train=transfer.fit_transform(x_train)#通过transform进行转换
x_test=transfer.fit_transform(x_test)
x_train

estimator=Ridge()#实例化一个对象
estimator.fit(x_train,y_train)#训练
print("这个模型的偏置是：\\n",estimator.intercept_)

#预测值和准确率
y_pre=estimator.predict(x_test)
print("预测值:\\n",y_pre)
score=estimator.score(x_test,y_test)
print("准确率：\\n",score)
#均方误差
ret=mean_squared_error(y_test,y_pre)#输出测试的目标值和预测后的预测值
print("均方误差是:\\n",ret)

部分输出

这个模型的偏置是：
 22.766336633663393
预测值:
 [23.72931449 14.23876947 20.82065099 20.37737003 41.32444418 31.51760466
	...
 21.48186817 17.7898301  31.19063626 37.89683539 18.74776502 23.14688806]
准确率：
 0.7461774619211063
均方误差是:
 21.375226392907397

3.2 API——RidgeCV

这个API封装的更牛逼：可以把λ对应的值，可以通过网格搜索进行值的传递

sklearn.linear_model.RidgeCV(_BaseRidgeCV, RegressorMixin)

1. 具有L2正则化的线性回归，可以进行交叉验证

2. coef_:回归系数

代码

from sklearn.datasets import load_boston#导入数据
from sklearn.model_selection import train_test_split#数据集划分
from sklearn.preprocessing import StandardScaler#特征工程标准化
from sklearn.linear_model import RidgeCV#岭回归
from sklearn.metrics import mean_squared_error#模型评估

boston=load_boston()
boston

#数据集划分
x_train, x_test, y_train, y_test = train_test_split(boston.data,boston.target,test_size=0.2)
x_train

transfer=StandardScaler()#实例化一个对象
x_train=transfer.fit_transform(x_train)#通过transform进行转换
x_test=transfer.fit_transform(x_test)
x_train

estimator=RidgeCV(alphas=(0.001,0.1,1,1.0))#实例化一个对象,自动选择一个参数看看那个最好
estimator.fit(x_train,y_train)#训练
print("这个模型的偏置是：\\n",estimator.intercept_)

#预测值和准确率
y_pre=estimator.predict(x_test)
print("预测值:\\n",y_pre)
score=estimator.score(x_test,y_test)
print("准确率：\\n",score)
#均方误差
ret=mean_squared_error(y_test,y_pre)#输出测试的目标值和预测后的预测值
print("均方误差是:\\n",ret)

部分输出

这个模型的偏置是：
 22.54529702970301
预测值:
 [20.80073917 22.01968705 22.07129549 13.1739321  29.19152411 33.26611376
	...
 31.36346221 25.80495191 10.39900086 25.39191069 16.09318826 24.79786881]
准确率：
 0.7216861974681366
均方误差是:
 23.6001418609719

三. 欠拟合

1. 效果：训练误差和测试误差都很够大

2. 原因：学习数据特征少

3. 解决：添加多项式特征，添加其他特征项

本人博客：https://blog.csdn.net/weixin_46654114
本人b站求关注：https://space.bilibili.com/391105864
转载说明：跟我说明，务必注明来源，附带本人博客连接。

请给我点个赞鼓励我吧