pytorch入门线性代数的实现

Posted 2021-05-21 啊～小 l i

线性代数

标量：只有一个元素的张量表示

import torch

x = torch.tensor([3.0])
y = torch.tensor([2.0])
print(x+y)
print(x*y)
print(x/y)
print(x**y)

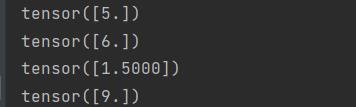
向量：标量值组成的列表

z = torch.arange(4)
print(z)
print(z[3])

通过张量的索引访问任意一元素

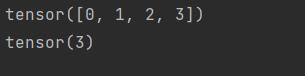
通过指定两个分量m n来创建一个形状为m*n的矩阵

h = torch.ones(25).reshape(5,5)
print(h)

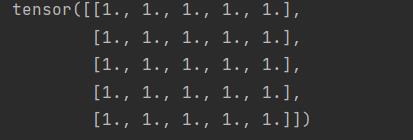
print(len(h))  # 张量大小
print(h.shape)  # 张量形状

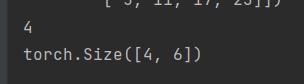
矩阵的转置

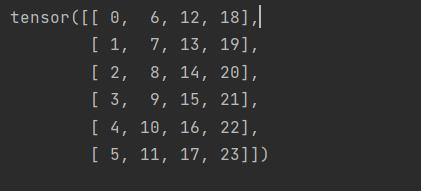
h = torch.arange(24).reshape(4,6)
print(h.T)

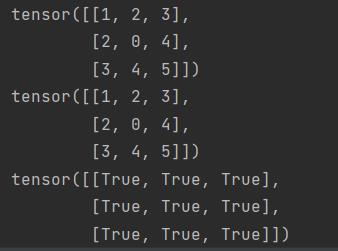
• 对称矩阵(A == A.T)

B = torch.tensor([[1,2,3],[2,0,4],[3,4,5]])
print(B)
print(B.T)
print(B == B.T)

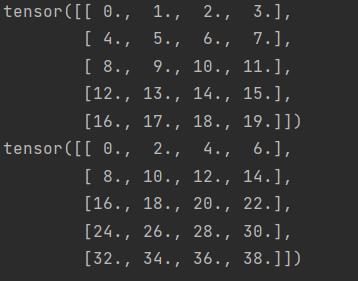
• 通过分配新的内存，实现张量复制

j = torch.arange(20, dtype=torch.float32).reshape(5,4)
k = j.clone()  # 将j的副本分配给k
print(k)
print(j+k)

两个矩阵按照元素的乘法称为 哈达玛积

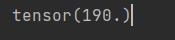
• 求矩阵所有元素的和
  print(j.sum())
  

a = torch.arange(20*2).reshape(2,5,4)
print(a.shape)
print(a.sum())

• 指定求和张量的轴

a = torch.arange(20*2).reshape(2,5,4)
print(a.shape)
print(a.sum())
print(a)
print(a.sum(axis=0))
print(a.sum(axis=1))

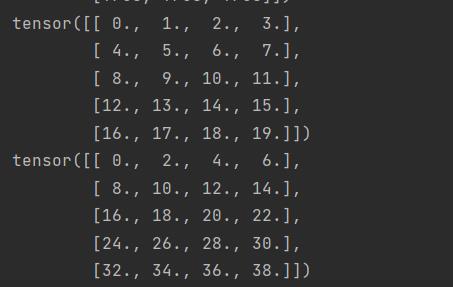
axis0：缩小了2这个维度，即上图的两个张量相加
axis0：缩小了5这个维度，即上图每个表的列相加
print(a.sum(axis=[0,1]))综合了上面两个实例

• 求平均值
  print(a.sum()/a.numel())等价于print(a.mean())
print(a.mean(axis=0))等价于print(a.sum(axis=0)/a.shape[0])

• 计数求和时保持轴数不变
  print(a.sum(axis=1,keepdims=True))
  轴数改变
  
  轴数不变
  

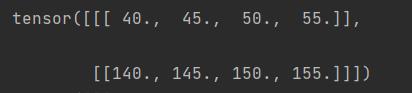
• 通过广播将a/a.sum()
  print(a/a.sum())

• 某个轴计算总和
  print(a.cumsum(axis=0))

• 点积（相同位置相乘）
  q1 = torch.ones(4,dtype=float32) q2 = torch.ones(4,dtype=float32) print(q1) print(q2) print(torch.dot(q1,q2))
  
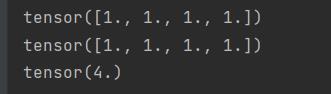
  等价于
  print(sum(q1*q2))

补充

用GPU存储张量
s = torch.randn(3000,3000,device="cuda:0") print(s)