R语言：作业八（用函数进行近似计算）

Posted 2021-05-21 fxalll

标题

• p103 8(2)
• p103 10
• p144 5
• p144 7
• p134 13

p103 8(2)

用模拟的方法近似计算下列积分，并和已知的精确答案进行比较：

${\int }_0^{\infty }x(1+x^3{)}^{-4}dx$

解答：

f1 = function(n,a,b,g){
	x = runif(n)
	sum((b-a)*g(a+(b-a)*x))/n
}
f = function(x) x*(1+x^3)^-4
f1(99999,0,Inf,f)

得到结果

[1]NaN

。因此我们需要近似计算积分。将Inf改为100试试：

[1] 0.2055264

我们使用integrate函数获得精确答案：

integrate(f,0,Inf)

0.2089975 with absolute error < 1.7e-05

误差不大。

p103 10

对(0,1)上的均匀随机变量U1、U2…，定义

N = m i n { n : ∑ i = 1 n U i > 1 } N=min \\{n:\\sum^{n}_{i=1} Ui>1\\} N=min{n:∑i=1n​Ui>1}.

即，N等于使其和超过1的随机数的个数。

解答：

这题比较简单，可以直接写：

f=function(x){
	EN = 0
	sumN = 0
	for(i in 1:x){
		N = 0
		i = 0
		while(N <= 1){
			rand = runif(1)
			N = N + rand
			i = i + 1
		}
		sumN = sumN + i
	}
	EN = sumN/x;EN
}

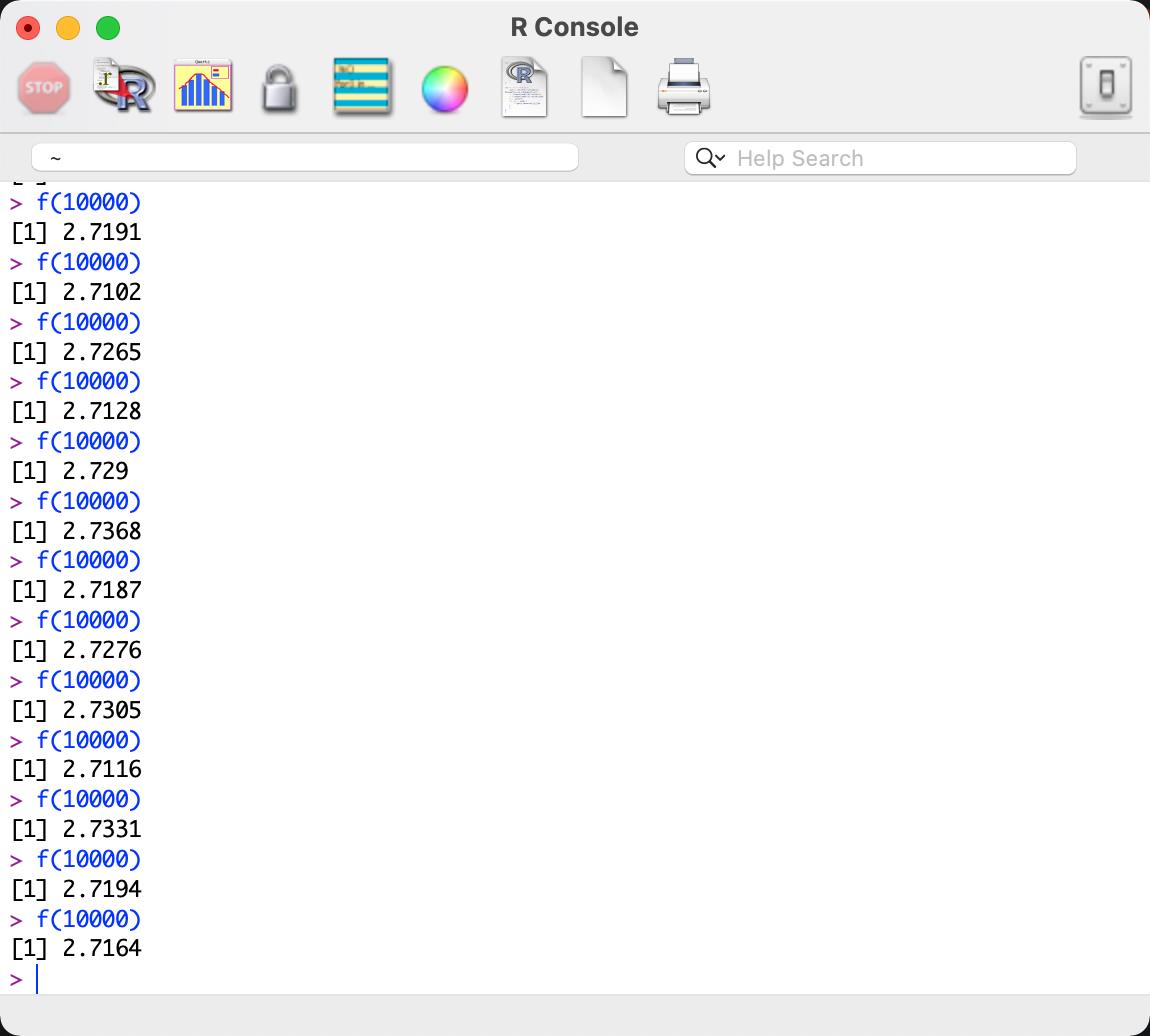
我猜理论值是2.72。

p144 5

在用随机投点法估计$pi$时，做多少次模拟才能获得一个长度小于0.1的区间，使之以95%的可靠性包括$pi$？

解答：
我们先写一个函数使用随机投点法估计pi。

f=function(x){
	k=9;u1=runif(x);u2=runif(x)
	X=2*u1-1;Y=2*u2-1
	for(i in 1:x){
		if(X[i]^2+Y[i]^2<=1) k=k+1
	}
	4*k/x
}

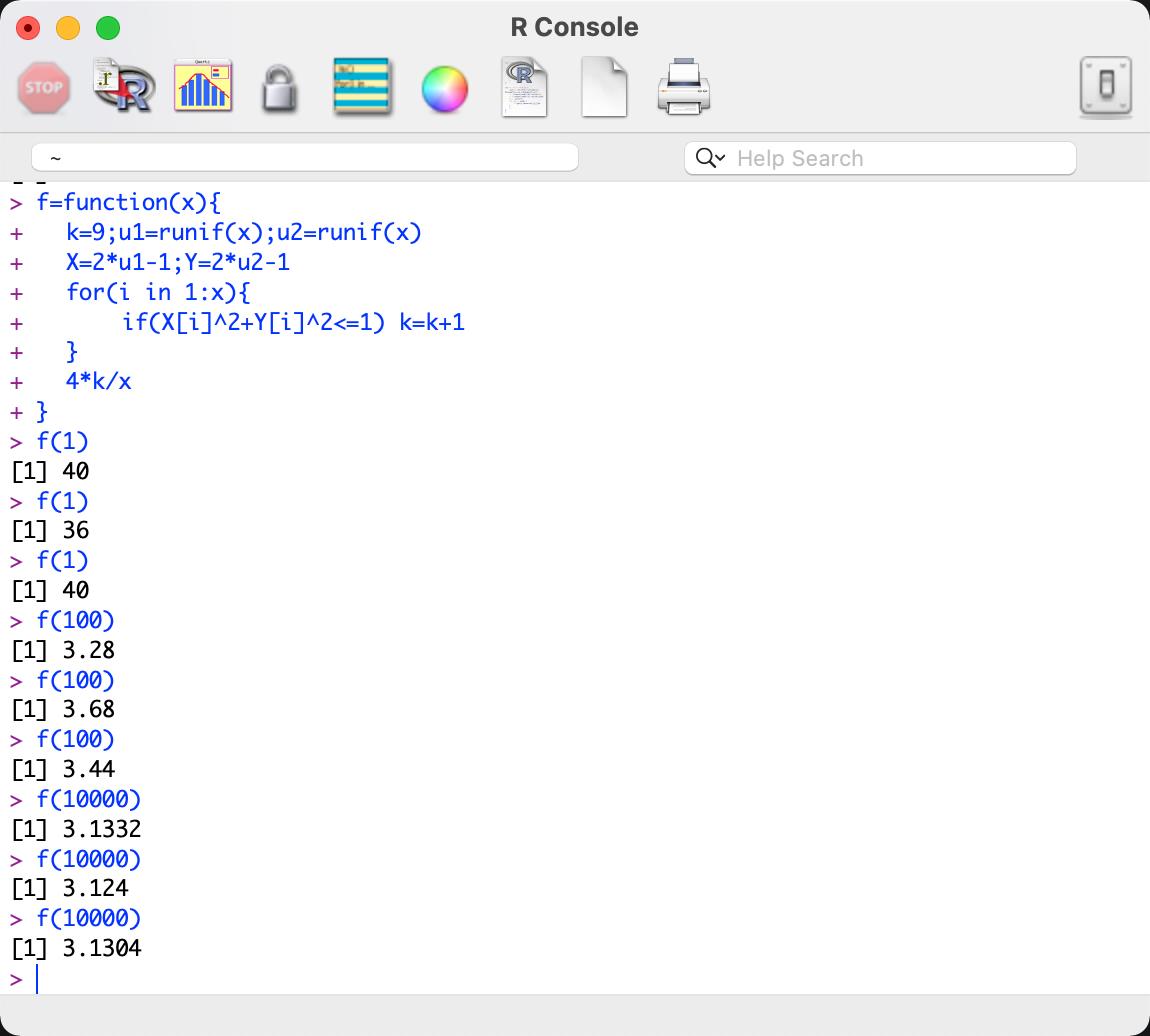
我们很容易可以写出测试程序：

f=function(x){
	k=9;u1=runif(x);u2=runif(x)
	X=2*u1-1;Y=2*u2-1;res=0;num=1
	for(i in 1:x){
		if(X[i]^2+Y[i]^2<=1) k=k+1
	}
	res=4*k/x
	while(abs(res-pi)>=0.1||abs((1-res/pi))>0.05){
		num = num + 1
		k=9;u1=runif(x);u2=runif(x)
		X=2*u1-1;Y=2*u2-1;res=0
		for(i in 1:x){
			if(X[i]^2+Y[i]^2<=1) k=k+1
		}
		res=4*k/x
	}
	res
}

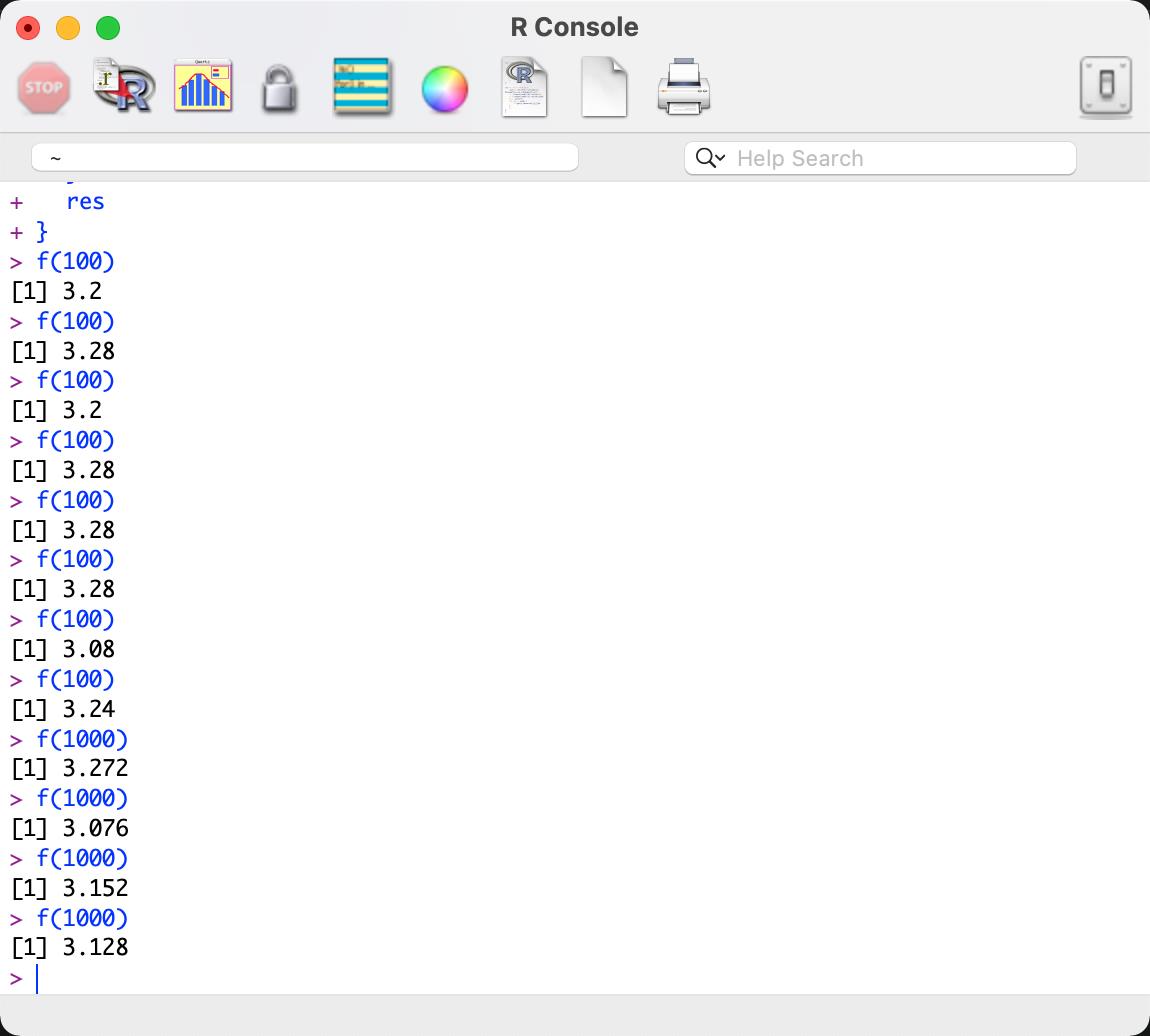
很明显，这一次所有的值都在题目范围内，接下来我们只需要输出模拟次数就可以了（把res改成num）：

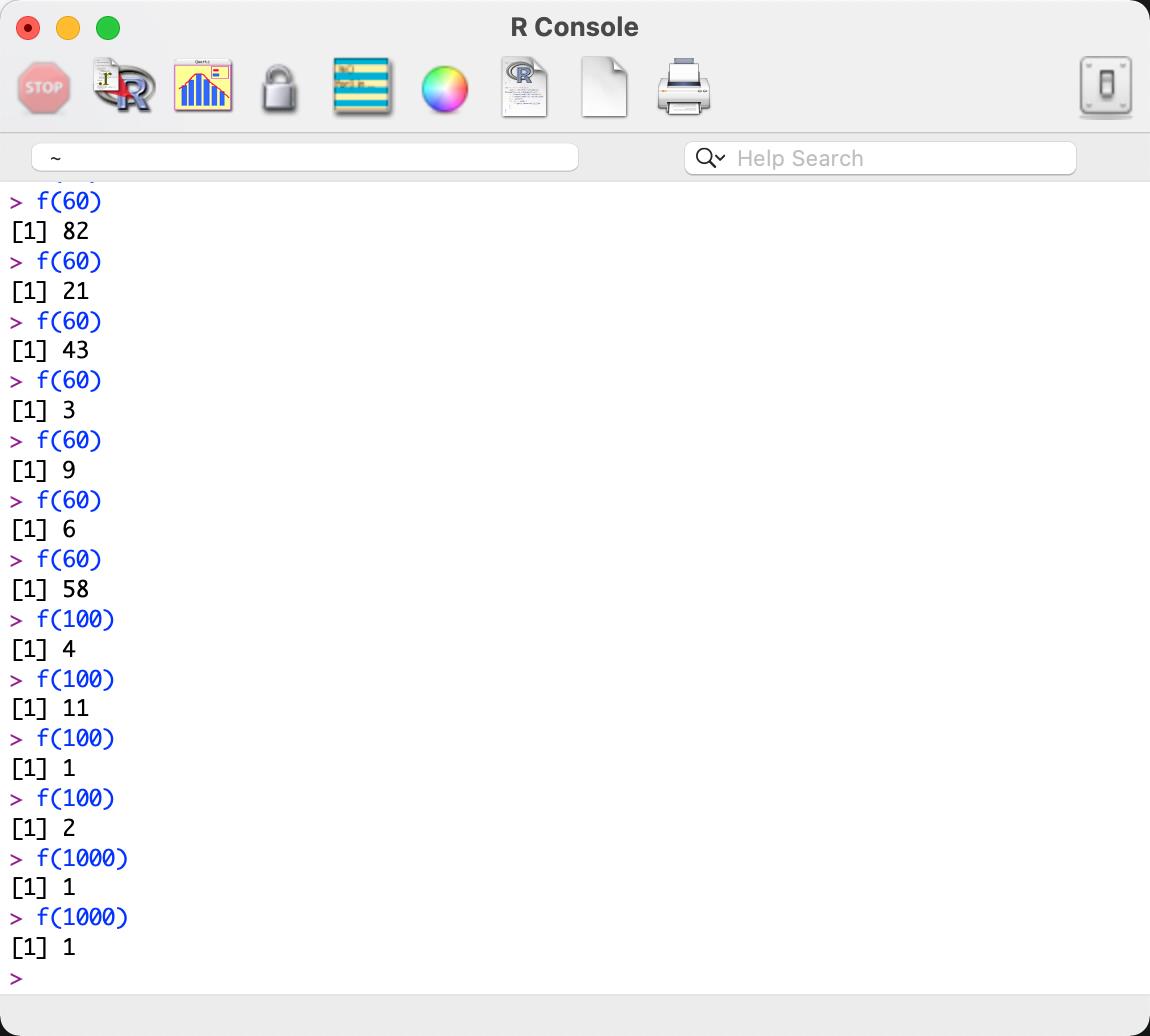
逐步更改x值，我们可以让它逐渐迅速而准确地得到pi值。（以上为改x值时对应的模拟次数）

p144 7

为了估计$\theta$，产生了20个相互独立的具有均值$\theta$的随机数，其值如下：

解答：

我们观察这组数字，得到其平均值为122.85，平均值与最值差为29.85。

我们不妨使用代码：

round(rnorm(20,122.85,29.85))

可以大致模拟。如果要确定置信系数为0.99长度为1的最终估计量，我们这组数据仍然是不够的。我们很容易写出：

f=function(x,adv,sd){
	sumN=sum(round(rnorm(x,adv,sd)))
	advN=sumN/x
	tryN=1
	while(abs(advN-adv)>1||abs(advN/adv)<0.99){
		tryN=tryN+1
		sumN=sum(round(rnorm(x,adv,sd)))
		advN=sumN/x
	}
	tryN
}

我们不妨假设$\theta$为120，标准差为30。

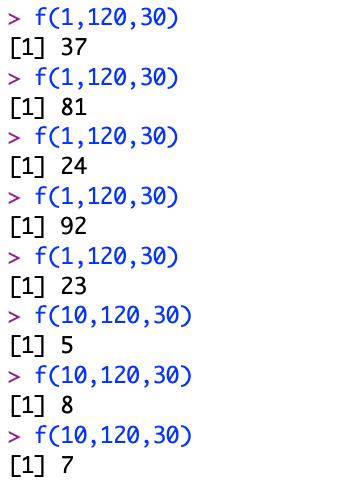
可以看出一个产生1个，由于达不到要求，会额外生成20～100不定的模拟次数才能最终达到要求。

如果一次产生10个，大约需要产生70～80个随机数。

p134 13

一个意外伤亡保险公司有1000个客户，每个客户独立地在下个月以概率0.05索赔.假设索赔量是独立的具有均值$ 800指数随机变量.用模拟方法估计这些索赔量的和超过$ 50000 的概率。

解答：

作1000次模拟，设X为下个月需要索赔的客户数， 易知X服从参数为(1000,0.05)的二项分布；设Y表示每个客户需要索赔的数额，由题意知，Y服从参数为1/800的 指数随机变量。所求的概率即：

k=0
for(i in 1:1000){
	X=rbinom(1,1000,0.05)
	Y=rexp(X,1/800)
	if(sum(Y)>50000){
		k=k+1
	}
}
k/1000

[1] 0.116