RBF预测基于混沌时间序列改进RBF神经网络实现预测matlab源码

Posted 2021-05-21 Matlab走起

RBF的直观介绍

RBF具体原理，网络上很多文章一定讲得比我好，所以我也不费口舌了，这里只说一说对RBF网络的一些直观的认识

1 RBF是一种两层的网络

是的，RBF结构上并不复杂，只有两层：隐层和输出层。其模型可以数学表示为：
y j = ∑ i = 1 n w i j ϕ ( ∥ x − u i ∥ 2 ) , ( j = 1 , … , p ) y_j = \\sum_{i=1}^n w_{ij} \\phi(\\Vert x - u_i\\Vert^2), (j = 1,\\dots,p)yj​=i=1∑n​wij​ϕ(∥x−ui​∥2),(j=1,…,p)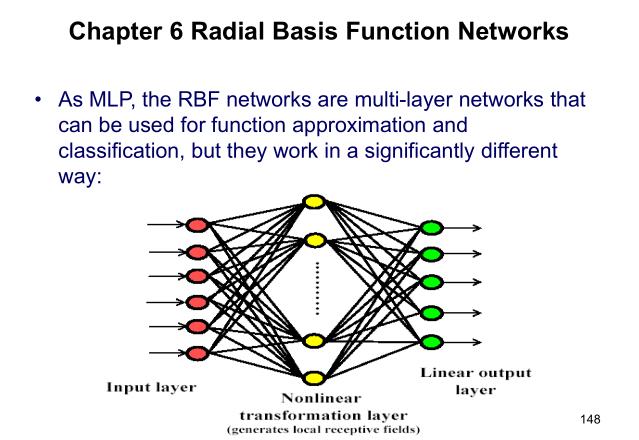

2 RBF的隐层是一种非线性的映射

RBF隐层常用激活函数是高斯函数：
ϕ ( ∥ x − u ∥ ) = e − ∥ x − u ∥ 2 σ 2 \\phi(\\Vert x - u\\Vert) = e^{-\\frac{\\Vert x-u\\Vert^2}{\\sigma^2}}ϕ(∥x−u∥)=e−σ2∥x−u∥2​

3 RBF输出层是线性的

4 RBF的基本思想是：将数据转化到高维空间，使其在高维空间线性可分

RBF隐层将数据转化到高维空间（一般是高维），认为存在某个高维空间能够使得数据在这个空间是线性可分的。因此啊，输出层是线性的。这和核方法的思想是一样一样的。下面举个老师PPT上的例子：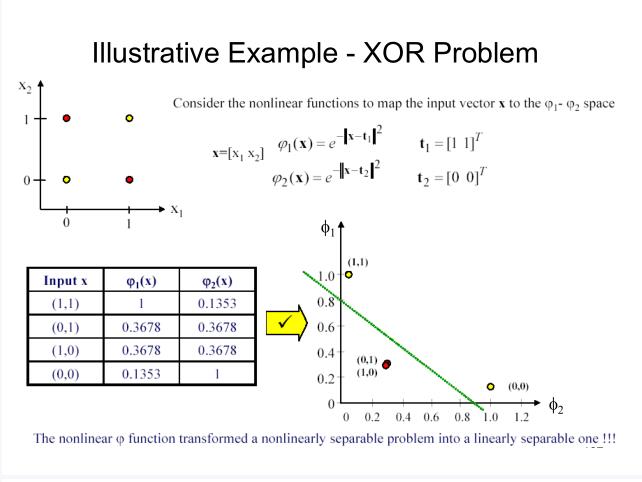

上面的例子，就将原来的数据，用高斯函数转换到了另一个二维空间中。在这个空间里，XOR问题得到解决。可以看到，转换的空间不一定是比原来高维的。

RBF学习算法

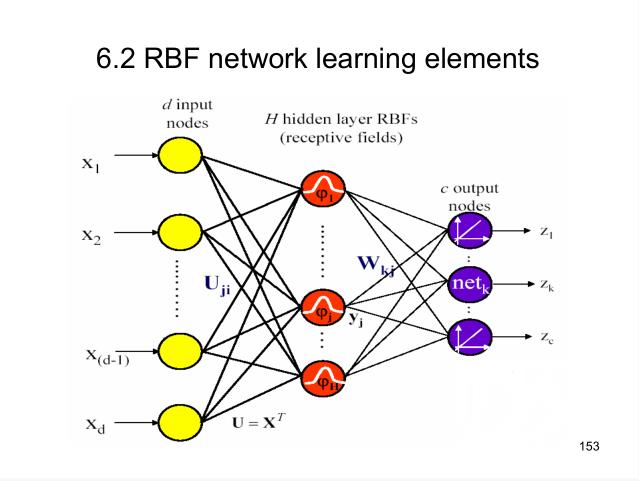
对于上图的RBF网络，其未知量有：中心向量u i u_iui​，高斯函数中常数σ \\sigmaσ，输出层权值W WW。
学习算法的整个流程大致如下图：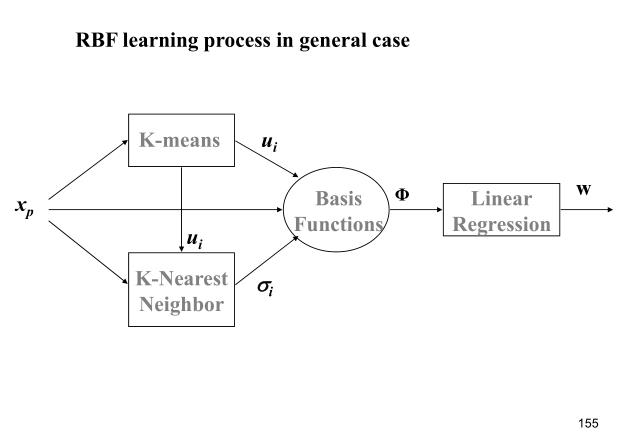

具体可以描述为：

1. 利用kmeans算法寻找中心向量u i u_iui​
2. 利用kNN(K nearest neighbor)rule 计算 σ \\sigmaσ
   σ i = 1 K ∑ k = 1 K ∥ u k − u i ∥ 2 \\sigma_i = \\sqrt{\\frac{1}{K}\\sum_{k=1}^K \\Vert u_k - u_i\\Vert^2}σi​=K1​k=1∑K​∥uk​−ui​∥2​
3. W WW可以利用最小二乘法求得

Lazy RBF

可以看到原来的RBF挺麻烦的，又是kmeans又是knn。后来就有人提出了lazy RBF，就是不用kmeans找中心向量了，将训练集的每一个数据都当成是中心向量。这样的话，核矩阵Φ \\PhiΦ就是一个方阵，并且只要保证训练中的数据是不同的，核矩阵Φ \\PhiΦ就是可逆的。这种方法确实lazy，缺点就是如果训练集很大，会导致核矩阵Φ \\PhiΦ也很大，并且要保证训练集个数要大于每个训练数据的维数。

MATLAB实现RBF神经网络

下面实现的RBF只有一个输出，供大家参考参考。对于多个输出，其实也很简单，就是W WW变成了多个，这里就不实现了。

demo.m 对XOR数据进行了RBF的训练和预测，展现了整个流程。最后的几行代码是利用封装形式进行训练和预测。

 
% 混沌时间序列的 rbf 预测(一步预测) -- 主函数
clc
clear all
close all
 
%--------------------------------------------------------------------------
% 产生混沌序列
% dx/dt = sigma*(y-x)
% dy/dt = r*x - y - x*z
% dz/dt = -b*z + x*y
 
sigma = 16;             % Lorenz 方程参数 a
b = 4;                  %                 b
r = 45.92;              %                 c            
 
y = [-1,0,1];           % 起始点 (1 x 3 的行向量)
h = 0.01;               % 积分时间步长
 
k1 = 30000;             % 前面的迭代点数
k2 = 5000;              % 后面的迭代点数
 
Z = LorenzData(y,h,k1+k2,sigma,r,b);
X = Z(k1+1:end,1);      % 时间序列
X = normalize_a(X,1);   % 信号归一化到均值为0,振幅为1
 
%--------------------------------------------------------------------------
% 相关参数
 
t = 1;                  % 时延
d = 3;                  % 嵌入维数
n_tr = 1000;            % 训练样本数
n_te = 1000;            % 测试样本数
 
%--------------------------------------------------------------------------
% 相空间重构
 
X_TR = X(1:n_tr);
X_TE = X(n_tr+1:n_tr+n_te);
figure,plot(1:1:n_tr,X_TR,'r');
hold on
plot(n_tr+1:1:n_tr+n_te,X_TE,'b');
hold off
 
[XN_TR,DN_TR] = PhaSpaRecon(X_TR,t,d);
[XN_TE,DN_TE] = PhaSpaRecon(X_TE,t,d);
 
%--------------------------------------------------------------------------
% 训练与测试
 
P = XN_TR;
T = DN_TR;
spread = 1;       % 此值越大,覆盖的函数值就大(默认为1)
net = newrbe(P,T,spread);
 
ERR1 = sim(net,XN_TR)-DN_TR;
err_mse1 = mean(ERR1.^2);
perr1 = err_mse1/var(X)
 
DN_PR = sim(net,XN_TE);
ERR2 = DN_PR-DN_TE;
err_mse2 = mean(ERR2.^2);
perr2 = err_mse2/var(X)
 
%--------------------------------------------------------------------------
% 结果做图
 
figure;
subplot(211);
plot(1:length(ERR2),DN_TE,'r+-',1:length(ERR2),DN_PR,'b-');
title('真实值(+)与预测值(.)')
subplot(212);
plot(ERR2,'k');
title('预测绝对误差')
 

完整代码或者代写添加QQ1575304183