优化求解禁忌搜索算法求解基站选址问题matlab源码

Posted 2021-05-21 Matlab走起

一、简介

 一、局部领域搜索

   又称爬山启发式算法，从当前的节点开始，和周围的邻居节点的值进行比较。如果当前节点是最大的，那么返回当前节点，作为最大值(即山峰最高点)；反之就用最高的邻居节点替换当前节点，从而实现向山峰的高处攀爬的目的。它是禁忌搜索的基础，TS算法是在其上改进而来。       

优点：

        1、容易理解，容易实现，具有较强的通用性；

        2、局部开发能力强，收敛速度很快。

缺点：

        1、全局开发能力弱，只能搜索到局部最优解；

        2、搜索结果完全依赖于初始解和邻域的映射关系。

通过针对爬山法的分析，提出了TS搜索算法：

        改进1：接受劣解。

        改进2：引入禁忌表。

        改进3：引入长期表和中期表。

二、TS算法的特点:       

1、基本思想——避免在搜索过程中的循环

2、只进不退的原则,通过禁忌表实现    

3、不以局部最优作为停止准则  

4、邻域选优的规则模拟了人类的记忆功能

        TS算法构成要素:       

    (1)编码方式

     将不相同的n件物品分为m组，可以用的编码：

   a、带分隔符的顺序编码

    以自然数1~n分别代表n件物品，n个数加上 m-1个分割符号混编在一起，随机排列。  如：1-3-4-0-2-6-7-5-0-8-9

   b、自然数编码

   编码的每一位分别代表一件物品，而每一位的值代表该物品所在的分组。

    如：1-2-1-1-2-2-2-3-3

    (2)初始解的获取

   可以随机给出初始解，也可以事先使用其他启发式等算法给出一个较好的初始解。  

    (3)移动邻域

   移动是从当前解产生新解的途径，例如上述问题中用移动s产生新解s(x)。   从当前解可以进行的所有移动构成邻域，也可以理解为从当前解经过“一步”可以到达的区域。

    (4)禁忌表

   禁忌表的作用：防止搜索出现循环​

   (1)记录前若干步走过的点、方向或目标值，禁止返回

   (2)表是动态更新的

   (3)表的长度称为Tabu-Size  

  禁忌表的主要指标（两项指标）

     禁忌对象：禁忌表中被禁的那些变化元素

     禁忌长度：禁忌的步数

  禁忌对象（三种变化）

     以状态本身或者状态的变化作为禁忌对象

     以状态分量以及分量的变化作为禁忌对象

     采用类似的等高线做法，以目标值变化作为禁忌对象

  禁忌长度:可以是一个固定的常数(T=c),也可以是动态变化的，可按照某种规则或公式在区间内变化。

  禁忌长度过短，一旦陷入局部最优点，出现循环无法跳出；

  禁忌长度过长，候选解全部被禁忌，造成计算时间较大，也可能造成计算无法继续下去。

    (5)渴望水平函数   

   A(x，s)一般为历史上曾经达到的最好目标值，若有C(s(x))<A(x，s)则S(x)是不受T表限制。即使s(x)∈T，仍可取        x=s(x)。A(x，s)称为渴望水平函数。

    (6)停止准则

    (1)给定最大迭代步数（最常用 ）

    (2)设定某个对象的最大禁忌频率。

    (3)设定适配值的偏离阈值。

 二、源代码

```c
function [MINL,MINZ,RESULT,best_so_far]=Tabusearch(CS,MS,Z,NT,TL)
hwait = waitbar(0,'正在初始化>>>>');
pause(1);
%把Z转换成q，即把点的位置转换成点的坐标和权值
q=[];
for ii=1:size(Z,2)
    q=[q;CS(Z(1,ii),:)];
end
%初始化禁忌表TA
TA=zeros(1,size(q,1));
TA(TA==0)=inf;
%初始化指针ptr
ptr=1;
waitbar(1/100,hwait,'开始计算>>>>');
[bestF]=findL(q,MS);
result(ptr)=bestF;
%开始搜索
while ptr<NT
    %调用neighbor函数求出邻域
    %并通过findL函数求出领域的所有代价L(i)
    [NEIBR]=neighbor(Z,CS);
    for i=1:size(NEIBR,3)
        Q=NEIBR(:,:,i);
        L(i)=findL(Q,MS);
    end
    %在L(i)中找出最小代价m，及其所在行TI，TI即应变动的点
    m=min(L);
    [x,TI]=find(L==m);
    %if和else之间表示特赦准则的情况
    if m<bestF
        bestF=m;
        sit=TI;
        TA=TA-1;
        TA(TA==0)=inf;
        TA(1,TI)=TL;        
    else%else之后的if表示TI未在禁忌表中标记
        if TA(1,TI)==inf        
            bestF=m;
            TA=TA-1;
            TA(TA==0)=inf;
            TA(1,TI)=TL;
            sit=TI;
        else%else之后表示TI在禁忌表中有标记，m不能用
            %转而找没有被标记的最优点
            [x,ti]=find(TA==inf);
            %如果ti为空，则所有情况被标记，只执行禁忌表-1
            if  isempty(ti)
                TA=TA-1;
                TA(TA==0)=inf;
            else
                %如果ti不为空，则找出未被标记情况中的最小代价解
                for j=1:size(ti)
                    mimi(j)=L(ti(j));
                end
                bestF=min(mimi);
                [x,t]=find(L==bestF);
                TA=TA-1;    
                TA(TA==0)=inf;
                TA(1,t)=TL;
                sit=t;
            end
        end
    end
```

三、运行结果

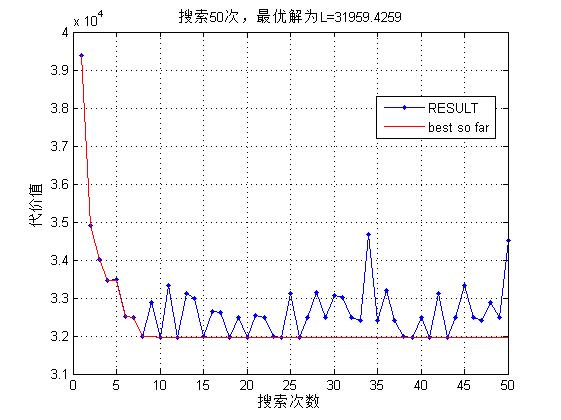
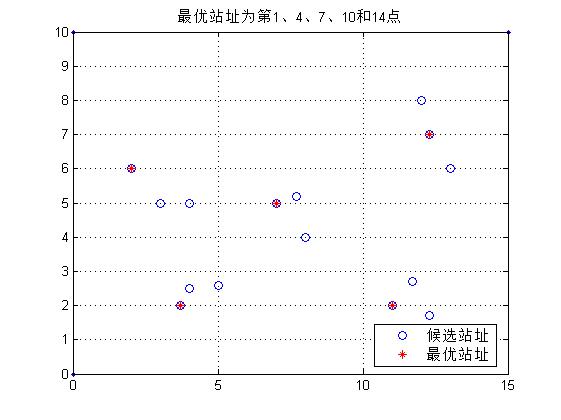
四、备注

完整代码或者仿真添加QQ1575304183