二叉树前中后序遍历_(非递归)
Posted LHlucky_2
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了二叉树前中后序遍历_(非递归)相关的知识,希望对你有一定的参考价值。
1. 前序遍历
-
Leetcode例题链接:link
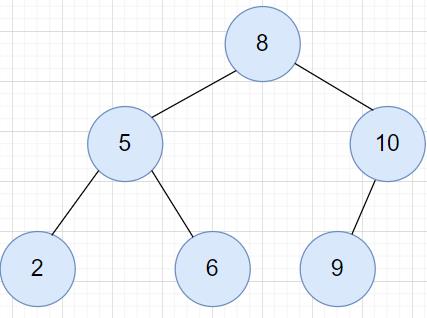
前序遍历:(根左右) -
8->5->2->6->10->9
用栈的非递归做法如下图所示:
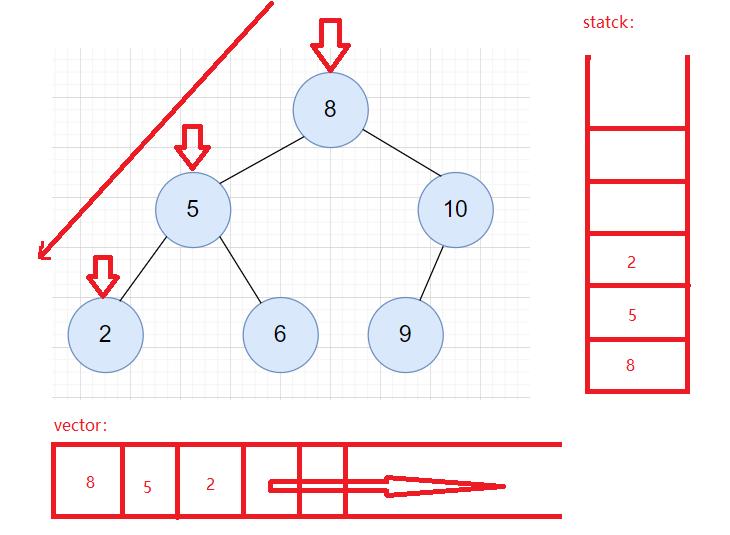
过程概述:
- 先将树从根节点开始往左遍历,将遍历的结点入栈,且遍历的时候将结点里面的值入到数组中(保证根先被存储)。
- 当走到最左边以后,开始访问栈顶元素。 并将栈顶元素删除(已经被存储过)。
- 然后让cur = top -> right,让栈顶元素的右树结点作为cur,则访问方式和刚才root结点的过程一二是一样的,(将右数作为一个新的树,在执行一二操作,子问题操作方法一样处理方式)。
代码实现:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
//二叉树的前序遍历非递归法。
//借助栈,先将树的所有左节点入栈,并将往左下走的时候的值保存到数组中。
vector<int> preorderTraversal(TreeNode* root) {
vector<int> vv;
stack<TreeNode*> st;
TreeNode *cur = root;
while(cur || !st.empty())
{
while(cur)
{
st.push(cur);
vv.push_back(cur->val);//先从前往左走,相当于先保留了根节点并且遍历了左节点 根左右。
cur = cur -> left;
}
TreeNode *top = st.top();//取栈顶元素,也就是树的最左结点。
st.pop();
cur = top -> right;//取最左结点的右结点。子问题一样的处理办法。
}
return vv;
}
};
代码二:(不做详解,可画图自行参悟,本人推荐上面方法)
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
stack<TreeNode*> st;
vector<int> ret;
if(root == nullptr)
{
return ret;
}
st.push(root);
while(!st.empty())
{
TreeNode *Node = st.top();
st.pop();
ret.push_back(Node->val);
if(Node->right)
st.push(Node->right);
if(Node->left)
st.push(Node->left);
}
return ret;
}
};
2. 中序遍历
-
Leetcode例题链接:link
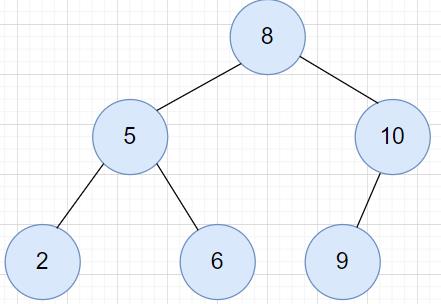
中遍历:(左根右) -
2->5->6->8->9->10
用栈的非递归做法如下图所示:
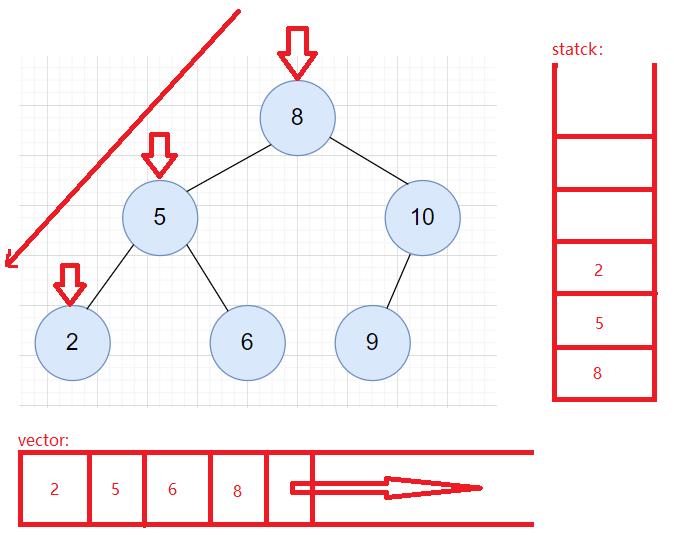
过程概述:
- 先将树从根节点开始往左遍历,将遍历的结点入栈,但遍历的时候将结点里面的值不入到数组中(和前序有差别的地方)。
- 当走到最左边以后,开始访问栈顶元素。并将栈顶元素的值入到数组中, 并将栈顶元素删除(保证左先被存储,且已经被存储过删除掉)。
- 然后让cur = top -> right,让栈顶元素的右树结点作为cur,则访问方式和刚才root结点的过程一二是一样的,(将右数作为一个新的树,在执行一二操作,子问题操作方法一样处理方式)。
代码实现:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
//二叉树中序遍历非递归法
//先将所有的左节点入栈,但是将值不放进数组中
vector<int> inorderTraversal(TreeNode* root) {
vector<int> vv;
stack<TreeNode*> st;
TreeNode *cur = root;
while(cur || !st.empty())
{
while(cur)
{
st.push(cur);
cur=cur->left;
}
//当把所有的左节点入栈以后,取栈顶元素就是最左结点,这个时候再把值入到子数组中。
TreeNode *top = st.top();
st.pop();
vv.push_back(top->val);
cur = top -> right;//左边处理结束以后再去处理右边子问题解决方法一样。
}
return vv;
}
};
代码二:(不做详解,可画图自行参悟,本人推荐上面方法)
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> ret;
stack<TreeNode*> st;
TreeNode* cur = root;
while(cur != nullptr || !st.empty())
{
if(cur != nullptr)
{
st.push(cur);
cur = cur->left;//左
}
else
{
cur = st.top();
st.pop();
ret.push_back(cur->val);//中
cur = cur->right;//右
}
}
return ret;
}
};
3. 后序遍历
- Leetcode例题链接:link
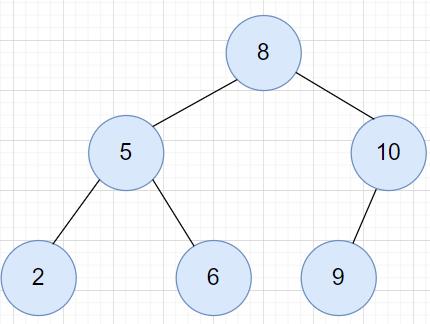
后序遍历:(左右根) - 2->6->5->9->10->8
用栈的非递归做法如下图所示:
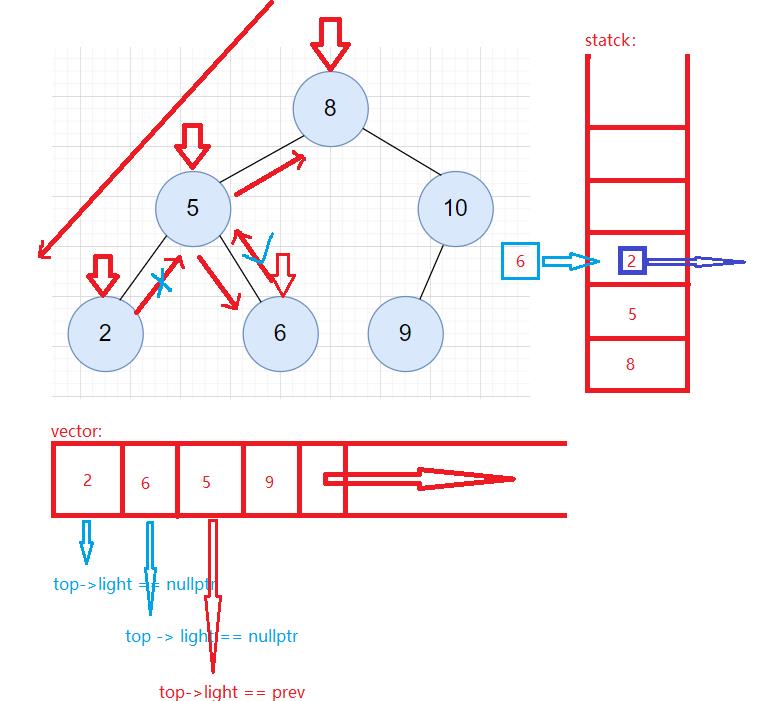
过程概述:
- 先将树从根节点开始往左遍历,将遍历的结点入栈,遍历的时候将结点里面的值不入到数组中。
- 当走到最左边以后,开始访问栈顶元素,
当栈顶元素top -> light == nullptr时 将栈顶元素的值入到数组中,并将top结点删除。(先入左结点的值) - 则下一个栈顶元素时父结点,判断父结点有没有右树,如果有右数,则将这个结点的值不入数组,先访问右数结点,并将访问的结点由prev保存。
当top->light==prev时则说明父节点是第二次访问且右数已经访问完毕。(保证左右根) - 以上两个条件都不满足让cur = top -> right,让栈顶元素的右树结点作为cur,则访问方式和刚才root结点的过程一二是一样的,(将右数作为一个新的树,在执行一二操作,子问题操作方法一样处理方式)。
代码实现:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
vector<int> vv;
stack<TreeNode*> st;
TreeNode *prev = nullptr;//记录之前访问的结点为记录夫结点是第几次访问做准备
TreeNode*cur = root;
while(cur || !st.empty())
{
while(cur)//先入左节点
{
st.push(cur);
cur = cur -> left;
}
TreeNode *top = st.top();
if( top->right == nullptr || top -> right == prev)//数组入数据的条件
{
vv.push_back(top -> val);
st.pop();
prev = top;//记录访问结点,为了判断top -> right == prev做准备。
cur = nullptr;
}
else
{
cur = top -> right;
}
}
return vv;
}
};
代码二:(不做详解,可画图自行参悟,本人推荐上面方法)
/**
1. Definition for a binary tree node.
2. struct TreeNode {
3. int val;
4. TreeNode *left;
5. TreeNode *right;
6. TreeNode() : val(0), left(nullptr), right(nullptr) {}
7. TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
8. TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
9. };
*/
//递归法,利用前序遍历,中左右,改变为中右左,在一反转。左右中即可。
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
vector<int> ret;
stack<TreeNode*> st;
if(root)
{
st.push(root);
}
while(!st.empty())
{
TreeNode* Node = st.top();
st.pop();
ret.push_back(Node->val);//处理中值。
if(Node->left)//后处理左,则先入左。
{
st.push(Node->left);
}
if(Node->right)//先处理右,则后入右。
{
st.push(Node->right);
}
}
reverse(ret.begin(),ret.end());
return ret;
}
};
总结:
- 以上代码的总体框架基本一样,只是在往数组中入结点值的时机和条件有所差异。
- 本人推荐每种遍历的代码一,代码风格相似,掌握一种,别的都可以掌握。
- 每种遍历的代码二也是非递归遍历,也很简单,不做详解,可画图模拟。
以上是关于二叉树前中后序遍历_(非递归)的主要内容,如果未能解决你的问题,请参考以下文章