论文笔记---ClusterGAN: Latent Space Clustering in Generative Adversarial Networks
Posted 小葵花幼儿园园长
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了论文笔记---ClusterGAN: Latent Space Clustering in Generative Adversarial Networks相关的知识，希望对你有一定的参考价值。
前提知识
Abstract
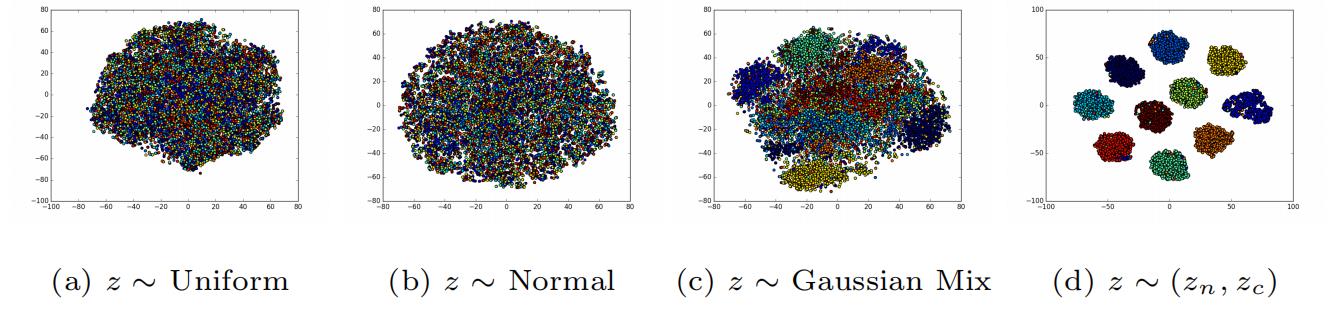
简单来说，本论文研究基于GAN的无监督分类问题，GAN的潜变量保留数据信息，但是数据的分布往往是平滑的，比如上图©,这种情况对于无监督分类任务十分不友好，针对上述问题提出了ClusterGAN。贡献如下：
- 利用一个混合的离散和连续潜变量（
one-hot编码和正态随机变量），以创建一个非光滑几何潜空间——图1-（d）。这样做的目的就是既保证良好的类间插值（正态随机变量），又能实现更好地聚类效果（one-hot编码）。 - 由于上述问题是非凸的，使用一种新的反向传播算法，它能适应离散-连续混合的情况，并给出了一个显式的逆映射网络来获得给定数据点的潜在变量。
- 将GAN与反映射网络联合训练，并以特定于簇的损耗来训练，这样投影空间中的距离几何就能反映出变量的距离几何。
Method
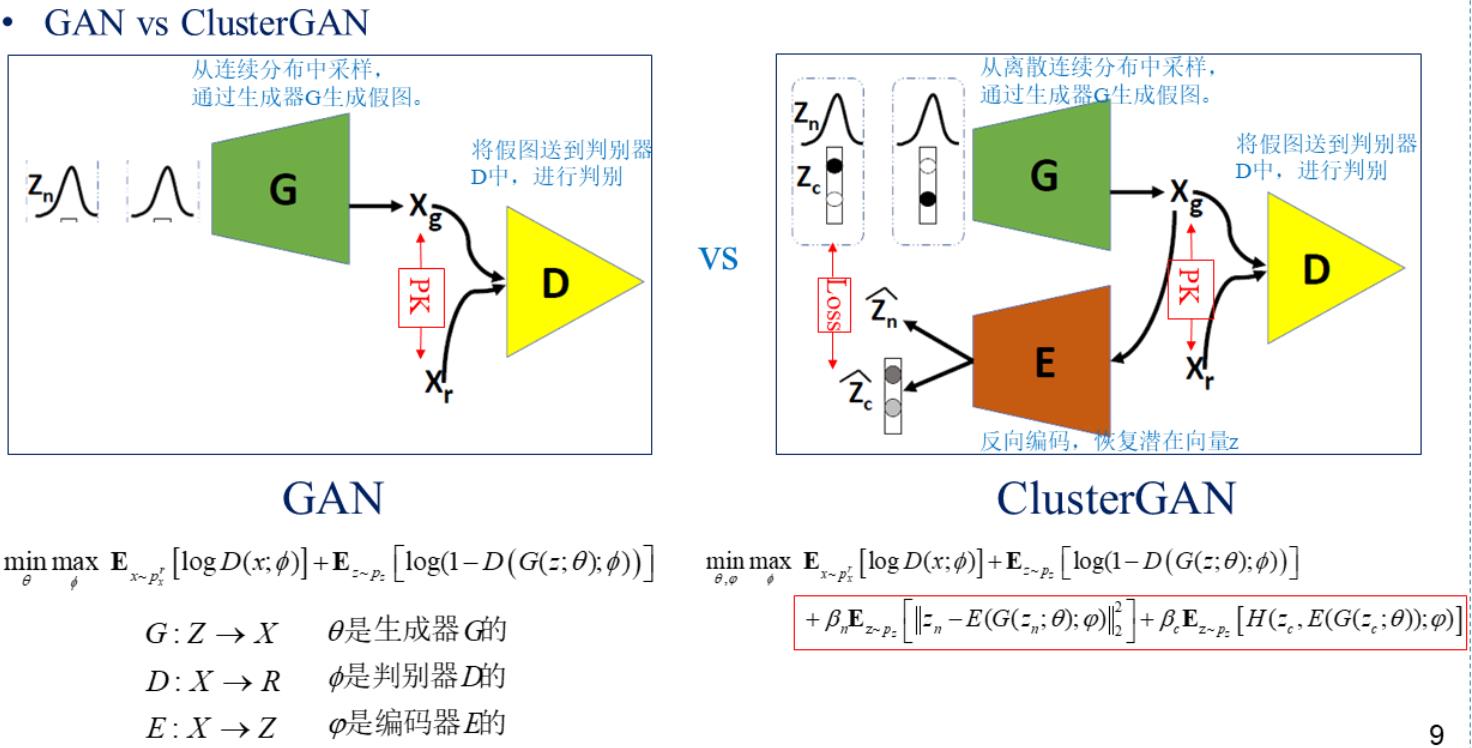
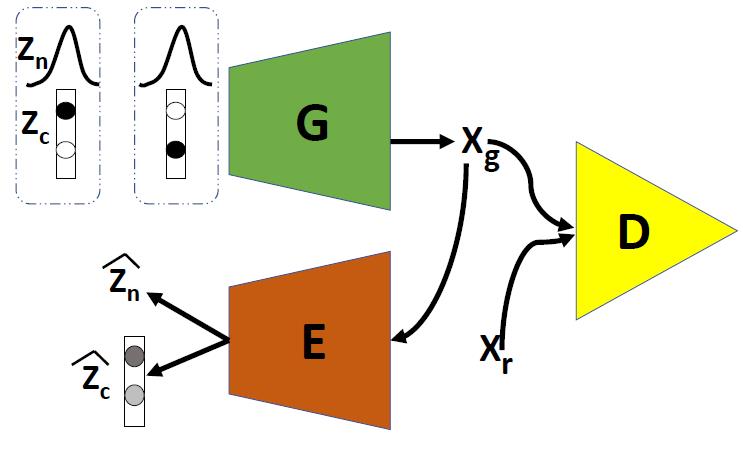
- Generator + Discriminator + Encoder
- encoder — 用于精确恢复潜在向量。
- 首先从离散连续分布中采样，通过生成器G生成fake-image，将fake-image分别输入到判别器D和编码器E中，在D中判别，在E中奖fake-image反向解码为 z n 和 z c z_n 和 z_c zn和zc
对于GAN网络来说生成器表示潜在空间到数据空间的映射 Z → X Z\\rightarrow X Z→X；判别器表示数据空间到真实值的映射 X → R X\\rightarrow R X→R 。
1. 采样
首先从正态随机变量和one-hot编码向量组成的先验 z z z中采样。
- z = ( z n , z c ) z = (z_n, z_c) z=(zn,zc)
- z n ∼ N ( 0 , σ 2 I d n ) z_n \\sim N(0, \\sigma ^2Id_n) zn∼N(0,σ2Idn)—正态随机分布
- z c = e k , k ∼ U { 1 , 2 , . . . K } z_c = e_k,k \\sim U\\begin{Bmatrix}1,2,...K\\end{Bmatrix} zc=ek,k∼U{1,2,...K}—one-hot编码向量，K是类别数。
- σ = 0.10 \\sigma = 0.10 σ=0.10 让潜在变量的每个维度以高概率满足 z n , j ⊆ ( − 0.6 ， 0.6 ) < < 1.0 ∀ j z_{n,j}\\subseteq(-0.6， 0.6)<< 1.0 \\forall j zn,j⊆(−0.6，0.6)<<1.0∀j
one-hot编码能够向GAN训练提供足够的信号使得每个模式仅从原始数据中的一个相应类生成样本。
2. 反向传播
传统的优化算法来解决
z
z
z 中的优化问题来恢复潜在向量 ：
z
∗
=
a
r
g
m
i
n
z
L
(
G
(
z
)
,
x
)
+
λ
∣
∣
z
∣
∣
p
z^* = argmin_zL(G(z),x) + \\lambda||z||_p
z∗=argminzL(G(z),x)+λ∣∣z∣∣p
即使反向传播是无损的，并且准确地恢复了潜在向量，这种方法也不足以对传统的潜在先验进行聚类。而且上面的优化问题在
z
z
z 上是非凸的。本文中使用
L
(
G
(
z
)
,
x
)
=
∣
∣
G
(
z
)
−
x
∣
∣
1
+
λ
∣
∣
z
n
∣
∣
2
L(G(z),x) = ||G(z) - x||_1 + \\lambda||z_n||_2
L(G(z),x)=∣∣G(z)−x∣∣1+λ∣∣zn∣∣2 ，而且使用
∣
∣
z
n
∣
∣
2
2
||z_n||_2^2
∣∣zn∣∣22 正则项惩罚仅仅正态随机变量。上述算法如下图。
5. 线性生成聚类
仅使用正态随机变量 z n z_n zn 进行聚类无法在线性生成的空间中恢复高斯数据的混合。 另外存在一个线性的G（·）将离散连续混合映射到高斯混合。
使用线性分类器可以获得更好的聚类效果
证明：
如果隐空间只包含连续部分，即
z
=
z
n
∼
N
(
0
,
σ
2
I
d
n
)
z=z_n\\sim N(0,\\sigma ^2I_{d_n})
z=zn∼N(0,σ2Idn)，则通过线性生成器只能生成高斯分布。（线性生成器的本质是一个线性变换，高斯分布经过线性变换后还是高斯分布，不能变为混合高斯分布）
如果隐空间包含离散和连续维混合，即
z
=
(
z
n
,
z
c
)
,
z
n
∼
N
(
0
,
σ
2
I
d
n
)
,
z
c
=
e
k
,
k
∼
U
{
1
,
2
,
.
.
.
,
K
}
z=(z_n,z_c),z_n\\sim N(0,\\sigma ^2I_{d_n}),z_c=e_k,k\\sim U\\left\\{1,2,...,K\\right\\}
z=(zn,zc),zn∼N(0,σ2Idn),zc=ek,k∼U{1,2,...,K}
要得到生成数据
X
∼
N
(
μ
ω
,
σ
2
I
d
n
)
,
ω
∼
U
{
1
,
2
,
.
.
.
,
K
}
X \\sim N(\\mu_{\\omega},\\sigma ^2I_{d_n}),\\omega \\sim U\\left\\{1,2,...,K\\right\\}
X∼N(μω,σ2Idn),ω∼U{1,2,...,K}，需要构造一个生成器
G
(
⋅
)
G(\\cdot)
G(⋅)，使得
G
：
Z
→
X
G：Z\\to X
G：Z→X，可以得到
x
g
=
G
(
z
)
=
G
(
z
n
,
z
c
)
=
z
n
+
A
z
c
x_g=G(z)=G(z_n,z_c)=z_n+Az_c
xg=G(z)=G(zn,zc)=zn+Azc,其中
A
=
d
i
a
g
[
μ
1
,
.
.
.
,
μ
K
]
A=diag[\\mu_1,...,\\mu_K]
A=diag[μ1,...,μK]是
K
×
K
K\\times K
K×K的对角矩阵。这里的X符合混合高斯分布。
6.插值
插值(Interpolation)是离散函数逼近的重要方法，利用它可通过函数在有限个点处的取值状况，估算出函数在其他点处的近似值。
clusterGAN中构造插值点是通过
z
=
(
z
n
,
μ
z
c
(
1
)
+
(
1
−
以上是关于论文笔记---ClusterGAN: Latent Space Clustering in Generative Adversarial Networks的主要内容，如果未能解决你的问题，请参考以下文章 菜鸡读论文Dive into Ambiguity: Latent Distribution Mining and Pairwise Uncertainty Estimation for Facia 论文导读Recovering Latent Causal Factor for Generalization to Distributional Shifts 论文导读Recovering Latent Causal Factor for Generalization to Distributional Shifts 变老 - 4 - Interpreting the Latent Space of GANs for Semantic Face Editing- 1 - 论文学习（人脸编辑）