C++代码用数组链表存储无向加权图有向加权图，小白都能看懂

Posted 2021-05-21 舒泱

目录

一、无向加权图

二、有向加权图

       

       

       

一、无向加权图

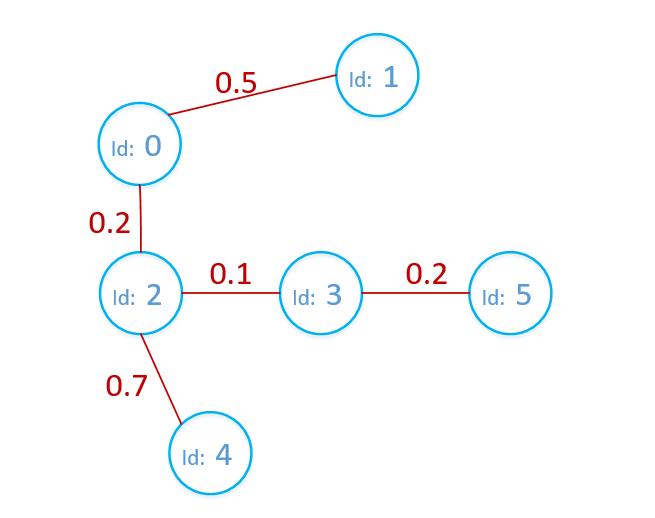
我们以下面这个无向加权图为例子

• 图中蓝色圆圈为顶点，红色线条为边
• 每个顶点有独一无二的id
• 边的权值可以相同，这个比较无所谓

       

下表是图的邻接矩阵：

• 表格第一行和第一列是顶点id
• 每个顶点和自己是相连的，此处用“\\”表示，顶点0和顶点5之间没有边，我这里用0表示，你也可以用一个不可能出现的边权值来表示两顶点间没有边
  

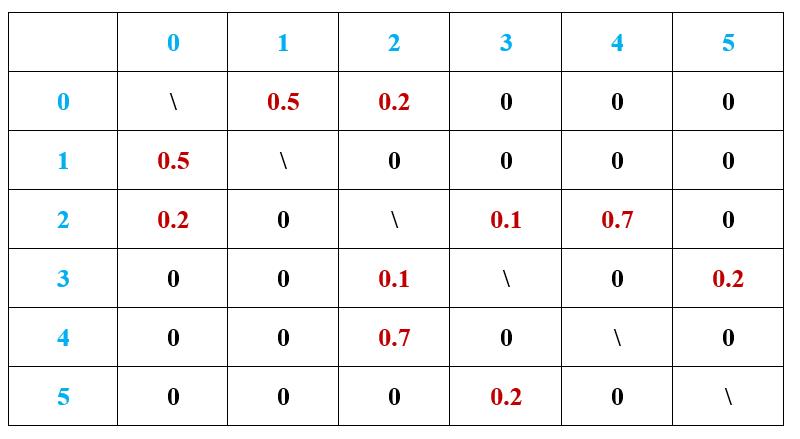
用二维数组存储图的邻接矩阵

• 非常简单，把上表的值依次存进去就是
• 但非常占空间
• 尤其当邻接矩阵是稀疏矩阵，矩阵中有大量的0，也就是图中实际上没有几条边，这时候要考虑用链表存储

       

       

用数组链表存储图

C++代码如下，结合后面的图看更容易理解

• 边节点 Edge_node
• 顶点节点 Vertex_node
• 图 My_graph

#include <iostream>
#include <vector>

using namespace std;

// 边节点
class Edge_node {
public:
	unsigned int vertex_id;        // 这条边连接的顶点的id
	double edge_data;                 // 边信息，如权重
	Edge_node* next{ nullptr };
	Edge_node() = default;
	Edge_node(unsigned int v_id, double edge_info) {
		this->vertex_id = v_id;
		this->edge_data = edge_info;
		next = nullptr;
	}
};

// 顶点节点
class Vertex_node {
public:
	unsigned int vertex_id;  // 当前顶点的id
	int vertex_data;         // 顶点数据
	Edge_node* first_edge_node{ nullptr };
	Vertex_node() = default;
	Vertex_node(unsigned int vertex_id ,int vertex_data) {
		this->vertex_id = vertex_id;
		this->vertex_data = vertex_data;
	}
};

// 图
class My_graph {
private:
	vector<Vertex_node> vertices;
public:
	My_graph() = default;
	void add_vertex(unsigned int vertex_id,int vertex_data);    // 添加顶点
	bool add_edge(unsigned int v1, unsigned int v2, double edge_data = 0); // 添加边
	~My_graph();
};

// 添加顶点
void My_graph::add_vertex(unsigned int vertex_id,int vertex_data) {
	vertices.push_back(Vertex_node(vertex_id,vertex_data));            
}

// 添加边
bool My_graph::add_edge(unsigned int v1, unsigned int v2, double edge_data) {
	// 注意：添加边前请确保两个顶点已添加，否则访问vertices[v1]和vertices[v2]会数组越界
	// 为v1顶点添加与v2之间的边
	Edge_node* p = new Edge_node(v2, edge_data);
	if (!p) {
		return false;
	}
	// 前插法插入边节点
	p->next = vertices[v1].first_edge_node;
	vertices[v1].first_edge_node = p;
	// 为v2顶点添加与v1之间的边
	p = new Edge_node(v1, edge_data);
	if (!p) { 
		return false; 
	}
	p->next = vertices[v2].first_edge_node;
	vertices[v2].first_edge_node = p;
	return true;
}

My_graph::~My_graph()
{
	// 回收new的那些边节点
	// 通过数组vertices访问到顶点节点，通过顶点节点访问到与该顶点相连的所有边节点，挨个回收
	int siz = vertices.size();
	for (int i = 0; i < siz; ++i) {
		// p是栈上的一个变量，p指向了new出来的堆上的一个边节点
		Edge_node* p = vertices[i].first_edge_node;   
		while (p != nullptr) {
			Edge_node* p_next = p->next;
			delete p;    // 回收p指向的那块堆内存
			p = p_next;  // 令p指向该边节点的下一个边节点
			cout << "删除节点" << endl; // 写这句只是为了调试的时候看内存有没有被回收成功
		}						
	}
}

int main() {
	My_graph* g1=new My_graph();
    // 添加顶点
	for (int i = 0; i < 6; ++i) {
		g1->add_vertex(i,i);
	}
	// 添加边
	g1->add_edge(0, 1, 0.5);
	g1->add_edge(0, 2, 0.2);
	g1->add_edge(2, 3, 0.1);
	g1->add_edge(2, 4, 0.7);
	g1->add_edge(3, 5, 0.2);

	delete g1;
	g1 = nullptr;
    system("pause");
}

       
       

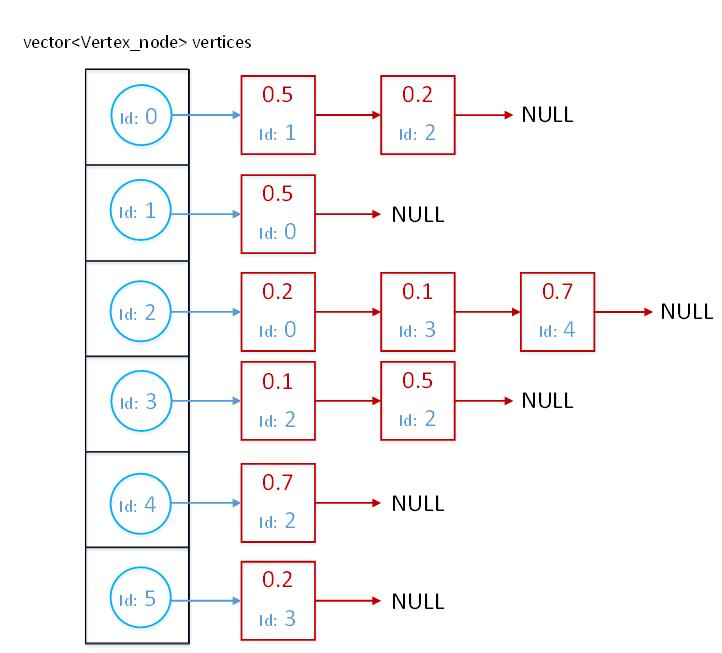
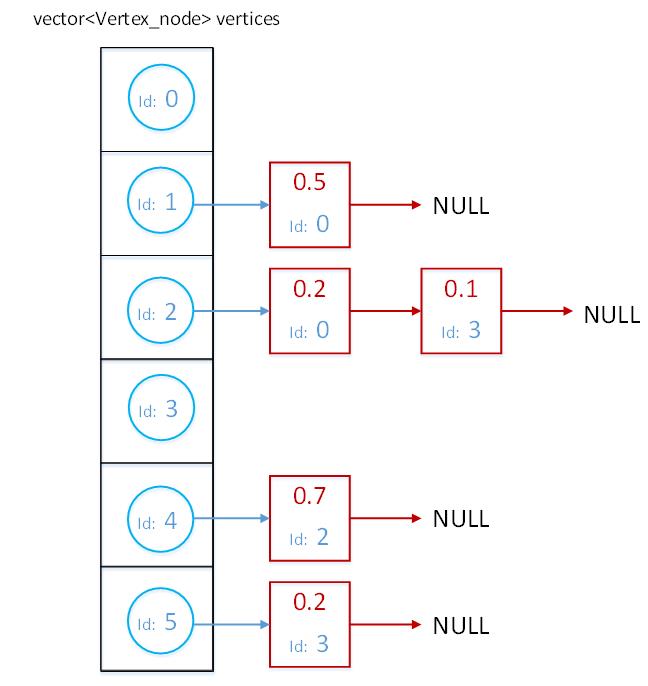
结合本文例子来看：

• 蓝色的是顶点节点，红色的是边节点
• 数组veetices中按id存储了所有顶点
• 顶点中有一个指针first_edge_node，指向了与该顶点相邻的某一条边，这个指针在图中我用蓝色画的。
• 边中有一个指针next，指向与该顶点相邻的其他边，这个指针在图中我用红色画的。

        例如，与顶点0相邻的顶点有顶点1、顶点2，图中顶点0指向边0.5，这个边节点内又存有这条边连接的另一端顶点的id 1，我们就知道顶点0和顶点1相邻，然后边权值为0.5。此外，边0.5内还有一个next指针，指向边0.2，这条边权值0.2，是顶点0和顶点2之间的边。

       

       

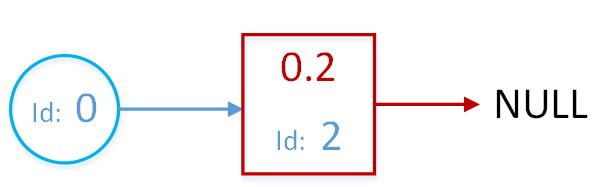
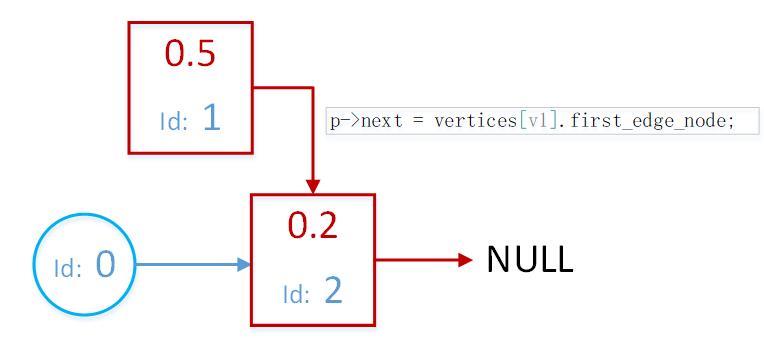
前插法插入边节点例子：

当前已有一条边：顶点0和顶点2之间的边，权值为0.2

       

现在要再添加一条边，顶点0和顶点1之间的边：

Edge_node* p = new Edge_node(v2, edge_data);
p->next = vertices[v1].first_edge_node;

       
       

vertices[v2].first_edge_node = p;

       

       

       

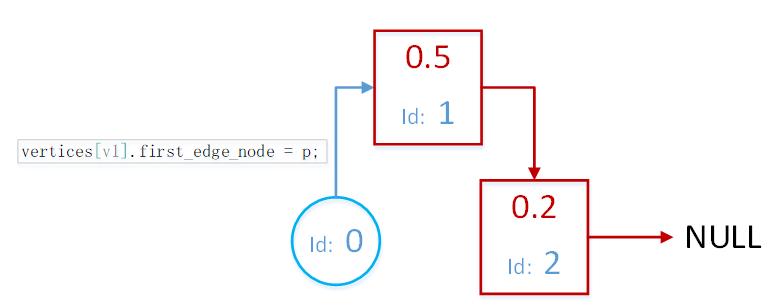
另外，由于建图时new了很多边节点，图对象析构时，应该在析构函数中回收这部分内存

        通过数组vertices访问到顶点节点，通过顶点节点访问到与该顶点相连的所有边节点，挨个回收

       

       

       

二、有向加权图

有向加权图与无向加权图类似，只是边有了方向，我们以下面这个有向加权图为例子

• 图中蓝色圆圈为顶点，红色线条为边
• 每个顶点有独一无二的id
• 边有方向，边的权值可以相同，这个比较无所谓
  

       

       
       

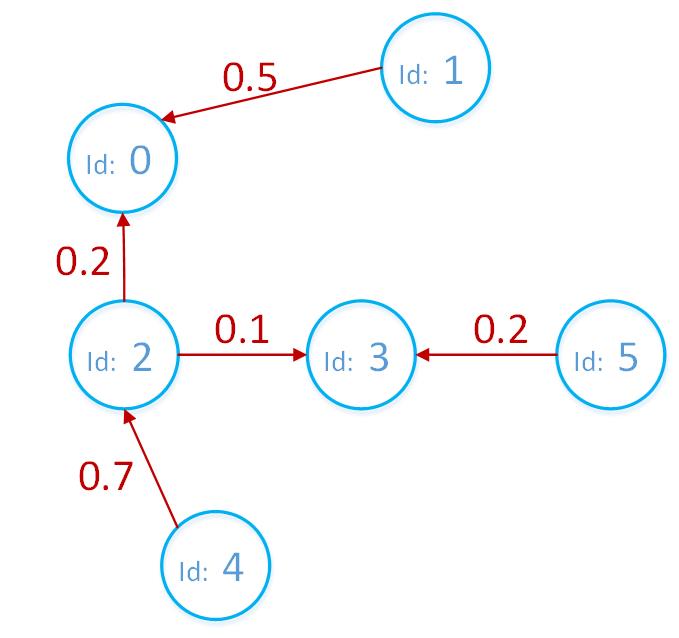
结合本文例子来看：

        例如，在无向加权图中，一条边在存储时，由于这条边即连接了顶点0又连接了顶点1，那么顶点0后应该有指针指向一个存储了id为1的边节点，顶点1后也应该有指针指向存储了id为0的边节点，也就是一条边在数组链表中被存储了两次。
        与无向加权图相比，有向加全图的边有了方向， 例如顶点0与顶点1之间的边是由1指向0的，只需要在顶点1后添加这个边节点就可以了，所以下图中，边节点少了一半。

       

C++代码也只需要改动图 My_graph中的增加边的函数，其余不变

// 添加边
bool My_graph::add_edge(unsigned int v1, unsigned int v2, double edge_data) {
	// 注意：添加边前请确保两个顶点已添加，否则访问vertices[v1]和vertices[v2]会数组越界
	// 为v1顶点添加指向v2之间的边
	// new一个边节点
	Edge_node* p = new Edge_node(v2, edge_data);
	if (!p) {
		return false;
	}
	// 前插法插入边节点
	p->next = vertices[v1].first_edge_node;
	vertices[v1].first_edge_node = p;
	return true;
}