图的存储方式——邻接矩阵和邻接表

Posted 2021-05-21 Rainbowman 0

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了图的存储方式——邻接矩阵和邻接表相关的知识，希望对你有一定的参考价值。

1. 基本概念

1.什么是图？

图由顶点和边组成，表示为G（V,E），其中G表示一个图，V是图G中顶点的集合，E是图G中边的集合。根据边是否有方向，可分为有向图和无向图。

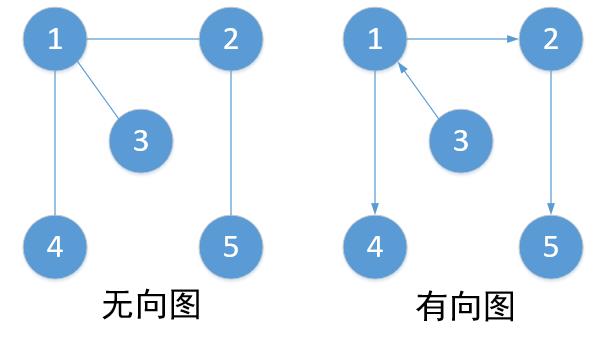
在这里插入图片描述

2. 邻接点

两结点之间通过边相连，则互为邻接点。如在上面的无向图中，（1，3），（2，5）等都为邻接点。

3. 顶点的度

顶点的度指的是与顶点v相连的边的数目。对于无向图来讲，只有度的概念，而对于有向图来讲，可分为入度和出度。入度是指向该顶点的边的条数，出度是从该顶点发出的边的条数。上面的有向图中，顶点1的入度为1，出度为2。

4. 权值

表示从一个顶点到另一个顶点的距离或耗费。

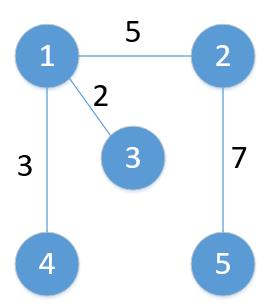
在这里插入图片描述
5. 连通性

对于两结点u，v，若通过u可到达v，则u和v是联通的。

在图 G 中，任意的结点vi,vj∈ V，有 vi,vj 连通，图 G 是连通的。

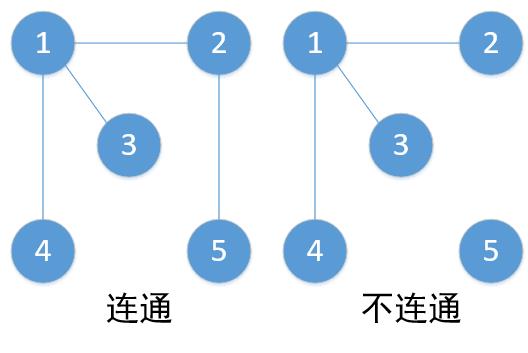
在这里插入图片描述

6. 连通分量

图中的极大联通子图。

2. 图的存储方式

图有两种常用的存储方式——邻接矩阵和邻接表

存储方式	思想
邻接矩阵	用一维数组存储结点，二维数组（行数=列数）存储边等信息
邻接表	用一维数组存储结点，链表存储邻接点等信息

2.1 邻接矩阵

思想

图的结点存储在一维数组Vex[] 内，另外有一二维数组 Edge[][] 来存储结点到结点的信息：若结点Vex[i]到Vex[j]存在一条边，权值为w，则Edge[i][j]=w，否则，Edge[i][j]=∞。

示意图

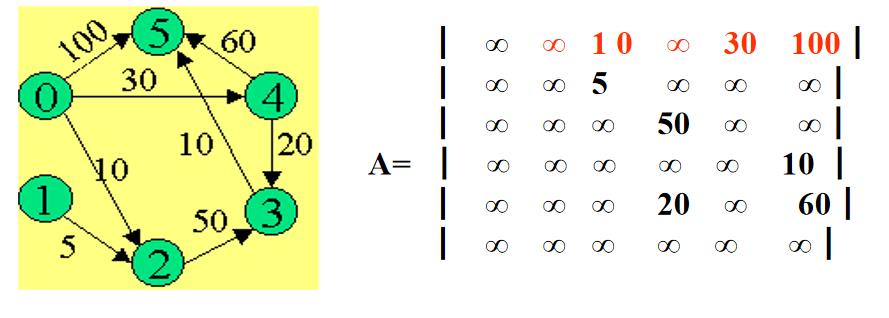
在这里插入图片描述
代码

#include <iostream>
#define INFINITY 99999
#define MAX_VEX_NUM 20
using namespace std;
typedef char NumType;
struct Graph
{
    NumType Vex[MAX_VEX_NUM];
    int Edge[MAX_VEX_NUM][MAX_VEX_NUM];
    int VexNum;
    int EdgeNum;
};
int Locate(Graph G,NumType v)
{
    int i;
    for(i=0;i<G.VexNum;i++)
        if(G.Vex[i]==v)return i;
    return -1;
}
void CreateGraph(Graph &G)
{
    cout<<"请输入结点个数和边的条数：";
    cin>>G.VexNum;
    cin>>G.EdgeNum;
    int i,j,k;
    for(i=0;i<G.VexNum;i++)
        for(j=0;j<G.VexNum;j++)G.Edge[i][j]=INFINITY;
    cout<<"请输入顶点信息：";
    for(i=0;i<G.VexNum;i++)cin>>G.Vex[i];
    cout<<"请输入边和权值：";
    int w;
    NumType v1,v2;
    for(k=0;k<G.EdgeNum;k++)
    {
        cin>>v1;cin>>v2;cin>>w;
        i=Locate(G,v1);j=Locate(G,v2);
        G.Edge[i][j]=w;
        //若为无向图需要加入下面代码
        //G.Edge[j][i]=G.Edge[i][j];
    }
    for(i=0;i<G.VexNum;i++)
    {
        for(j=0;j<G.VexNum;j++)cout<<G.Edge[i][j]<<" ";
        cout<<endl;
    }
}
int main()
{
    Graph G;
    CreateGraph(G);
    return 0;
}

2.2 邻接表

思想

图的结点使用一维数组Vex[]存储，邻接点用链表存储。

示意图

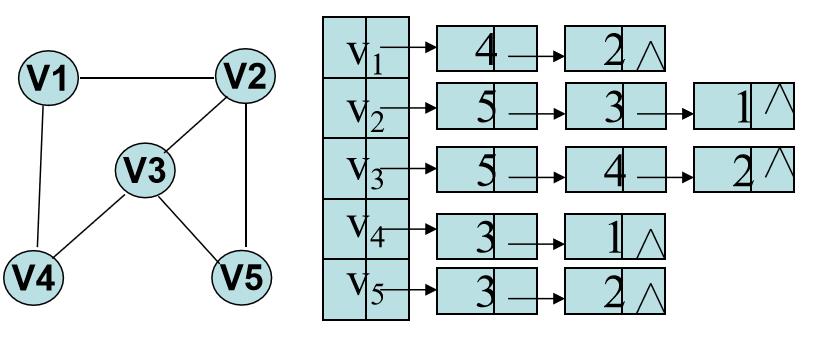
在这里插入图片描述
代码

#include <iostream>
#define MAX_VEX_NUM 20
using namespace std;
typedef char NumType;
struct EdgeNode
{
    int adjvex;
    EdgeNode *nextedge;
};
struct VexNode
{
    NumType data;
    EdgeNode *firstedgd;
};
struct Graph
{
    VexNode Vex[MAX_VEX_NUM];
    int VexNum;
    int EdgeNum;
};
int Locate(Graph G,NumType v)
{
    int i;
    for(i=0;i<G.VexNum;i++)
        if(G.Vex[i].data==v)return i;
    return -1;
}
void CreateGraph(Graph &G)
{
    cout<<"请输入结点个数和边的条数：";
    cin>>G.VexNum;cin>>G.EdgeNum;
    int i,j,k;
    cout<<"请输入结点信息：";
    for(i=0;i<G.VexNum;i++){cin>>G.Vex[i].data;G.Vex[i].firstedgd=0;}
    NumType v1,v2;
    for(k=0;k<G.EdgeNum;k++)
    {
        cin>>v1;cin>>v2;
        i=Locate(G,v1);j=Locate(G,v2);
        EdgeNode *p=new EdgeNode();
        EdgeNode *p0=new EdgeNode();
        *p={j,G.Vex[i].firstedgd};
        G.Vex[i].firstedgd=p;
        //如果是无向图需要加入下面代码
        //*p0={i,G.Vex[j].firstedgd};
        //G.Vex[j].firstedgd=p0;
    }
}
int main()
{
    cout << "Hello world!" << endl;
    return 0;
}