机器学习实战——分类及性能测量完整案例（建议收藏慢慢品）

Posted 2021-05-21 Dream丶Killer

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了机器学习实战——分类及性能测量完整案例（建议收藏慢慢品）相关的知识，希望对你有一定的参考价值。

文章目录

1. 获取数据
2. 训练二元分类器
3. 性能测量
4. 多类分类器
5. 误差分析
6. 多标签分类
7. 多输出分类

写在前面

参考书籍：Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow

❤ 本文为机器学习实战学习笔记，主要内容为第三章分类，文中除了书中主要内容，还包含部分博主少量自己修改的部分，如果有什么需要改进的地方，可以在 评论区留言 ❤。

❤更多内容❤

机器学习实战——房价预测完整案例（建议收藏慢慢品）

1. 获取数据

本文使用的是 MNIST 数据集，这是一组由美国高中生和人口调查局员工手写的 70000 个数字的图片。每张图片都用其代表的数字标记。它被誉为机器学习领域的 “Hello World” 。我们可以直接通过 Scikit-Learn 来获取 MINST 数据集。

from sklearn.datasets import fetch_openml
mnist = fetch_openml('mnist_784', version=1, as_frame=False)
# 获取mnist的键值
mnist.keys()

dict_keys([‘data’, ‘target’, ‘frame’, ‘categories’, ‘feature_names’, ‘target_names’, ‘DESCR’, ‘details’, ‘url’])

Scikit-Learn 加载的数据集通常具有类似的字典结构，包括

DESCR：描述数据集。
data：包含一个数组，每个实例为一行，每个特征为一列。
target：包含一个带有标记的数组。

# 获取特征与标签
X, y = mnist["data"], mnist["target"]
print(X.shape, y.shape)

(70000, 784) (70000,)

数据集共有 7 万张图片，每张图片有 784 个特征。图片为 28×28 像素，每个特征代表一个像素点的强度，从 0 （白色）—— 255 （黑色）。我们可以先用 Matplotlib 来显示一张图片看一下。

import matplotlib as mpl
import matplotlib.pyplot as plt
from pathlib import Path

current_path = Path.cwd()

some_digit = X[0]
some_digit_image = some_digit.reshape(28, 28)
# 显示灰色图
plt.imshow(some_digit_image, cmap=mpl.cm.binary)
# 显示彩色图
# plt.imshow(some_digit_image)
plt.axis("off")

# 保存灰色图
plt.savefig(Path(current_path, "./images/some_digit_plot.png"), dpi=600)
# 保存彩色图
# plt.savefig(Path(current_path, "./images/some_digit_plot_colour.png"), dpi=600)
plt.show()

灰色图

彩色图

我们看一下它对应的标签。

y[0]

‘5’

标签的结果与图片相符。

此时的标签是字符，需要转为整数。

import numpy as np

y = y.astype(np.uint8)

5

在进行之后的步骤之前，需先创建一个测试集，将它与训练集分开。

X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]

2. 训练二元分类器

我们先尝试训练一个区分两个类别：5 和非 5 的二元分类器，首先创建目标向量。

y_train_5 = (y_train == 5)    # [ True False False ...  True False False]
y_test_5 = (y_test == 5)

接着挑选一个分类器进行训练。一个好的选择随机梯度下降（ SGD ）分类器，它的优势在于：能够有效处理非常大型的数据集，这是由于 SGD 独立处理训练实例，一次一个实例（这也使得 SGD 非常适合在线学习）。先创建一个 SGDClassifier 并在整个训练集上进行训练。

from sklearn.linear_model import SGDClassifier

# 构建分类器
sgd_clf = SGDClassifier(max_iter=1000, tol=1e-3, random_state=42)
# 训练分类器
sgd_clf.fit(X_train, y_train_5)
# 预测
sgd_clf.predict([some_digit])

array([ True])

SGDClassifier 预测整个图像属于 5 ，结果正确，下面评估一下整个模型的性能。

3. 性能测量

3.1 交叉验证测量准确率

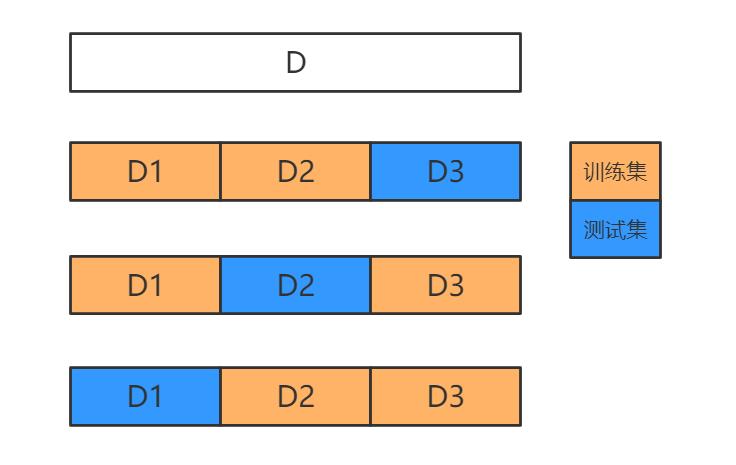
使用 Scikit-Learn 中的 cross_val_score() 函数来评估 SGDClassifier 模型，采用 K 折交叉验证法。这里使用 K=3 ，三个折叠，即将训练集分成 3 个折叠，每次留其中的 1 个折叠进行预测，剩余 2 个折叠用来训练，共重复 3 次。
在这里插入图片描述

from sklearn.model_selection import cross_val_score

# 交叉验证获取每次的模型准确率
cross_val_score(sgd_clf, X_train, y_train_5, cv=3, scoring="accuracy")

array([0.95035, 0.96035, 0.9604 ])

3 次交叉验证的结果看上去都不错，超过 95%，但事实真的如此？下面构建一个只预测非 5的分类器，我们看一下它交叉验证的评估结果。

from sklearn.base import BaseEstimator

# 构建分类器
class Never5Classifier(BaseEstimator):
    def fit(self, X, y=None):
        pass
    def predict(self, X):
        # 返回全1的数组
        return np.zeros((len(X), 1), dtype=bool)

never_5_clf = Never5Classifier()
cross_val_score(never_5_clf, X_train, y_train_5, cv=3, scoring="accuracy")

array([0.91125, 0.90855, 0.90915])

对于只预测非 5 的分类器，交叉验证的结果依旧很好，这说明训练集中大约只有 10% 的图片是数字 5。

我们看一下 y_train_5 中 非5 的比例是否在 90% 左右。

len(y_train_5[y_train_5==False]) / len(y_train_5)

0.90965

通过上面的结果，可以说明准确率往往无法成为分类器的首要性能指标，特别是在你处理不平衡的数据集时。

3.2 混淆矩阵

评估分类器性能的更好的方法是混淆矩阵。

混淆矩阵：统计A类别实例被分成B类别的次数

要计算混淆矩阵，需要先有一组预测才能将其与实际目标进行比较。当然可以通过测试集进行预测，但在目前阶段最好不要使用（测试集最好留到最后，在准备启动分类器时再使用）。我们可以使用 cross_val_predict() 函数来替代。

from sklearn.model_selection import cross_val_predict

y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3)
print(y_train_pred)
y_train_pred.shape

输出
[ True False False … True False False]
(60000,)

与 cross_val_score() 函数一样， cross_val_predict() 函数同样执行K折交叉验证，但返回的不是评估分数，而是每个折叠的预测。

现在可以使用 confusion_matrix() 函数来获取混淆矩阵，只需要给出 y_train_5 （目标类别）和 y_train_pred（预测类别）即可。

from sklearn.metrics import confusion_matrix

confusion_matrix(y_train_5, y_train_pred)

输出

在进行下面内容之前要确保你已经了解以下含义：

TP（True Positive）：真正类，模型预测样本为正类，实际也是正类。
FP（False Positive）：假正类，模型预测样本为正类，实际上是负类。
TN（True Negative）：真负类，模型预测样本为负类，实际上也是负类。
FN（True Negative）：假负类，模型预测样本为负类，实际上是正类。

我们将上面结果以图的形式展示出来。
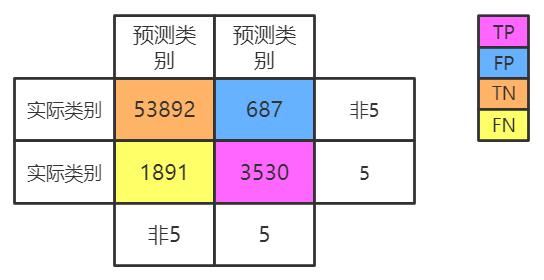
在这里插入图片描述
混淆矩阵中的行表示实际类别，列表示预测类别。图中我们可以得到以下信息：

在第一行表示所有实际类别是 非5 的图片中：
- 53892 张被正确的分为 非5 类别（真负类 TN ）
- 687 张被错误的分为 5 类别（假正类 FP）
在第一行表示所有实际类别是 5 的图片中：
- 1891 张被错误的分为 非5 类别（假负类 FN ）
- 3530 张被正确的分为 5 类别（真正类 TP ）

一个完美的分类器只有真正类和真负类，所以它的混淆矩阵只会在其对角线（左上——右下）上有非零值。如下所示：

 # 直接以实际标签作为预测结果，来塑造一个完美的分类结果
y_train_perfect_predictions = y_train_5
confusion_matrix(y_train_5, y_train_perfect_predictions)

输出

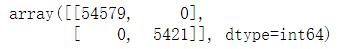3.3 精度和召回率

混淆矩阵确实能够提供大量的信息，但如果希望指标更简洁一些，分类器的精度可能更加适合。

精度：正类预测的准确率
$精度=\\cfrac{TP}{TP + FP}$
TP 是真正类的数量， FP 是假正类的数量。

精度通常和召回率一起使用。

召回率：正确检测到的正类实例的比率
$召回率=\\cfrac{TP}{TP + FN}$
TP 是真正类的数量， FN 是假负类的数量。

在 Scikit-Learn 中可以使用 precision_score ， recall_score 来计算精度和召回率。

from sklearn.metrics import precision_score, recall_score

print('精度：', precision_score(y_train_5, y_train_pred))
print('召回率：', recall_score(y_train_5, y_train_pred))

输出
精度： 0.8370879772350012
召回率： 0.6511713705958311

也可以使用混淆矩阵进行计算。结果一样。

cm = confusion_matrix(y_train_5, y_train_pred)

print('精度：', cm[1, 1] / (cm[0, 1] + cm[1, 1]))
print('召回率：', cm[1, 1] / (cm[1, 0] + cm[1, 1]))

输出
精度： 0.8370879772350012
召回率： 0.6511713705958311

根据精度和召回率的结果来看，它不再像准确率那么高了。当它预测一张图片为 5 时，他只有 83.7% 的概率是准确的，在整个测试集中也只有 65.1% 的 5 被正确检测出来。

3.4 $F_1$ 分数

我们可以将精度和召回率组合成一个指标，称为 $F_1$ 分数。

$F_1$ 分数：精度和召回率的谐波平均值
$F_1=\\cfrac{2}{\\cfrac{1}{精度} + \\cfrac{1}{召回率}}=\\cfrac{TP}{TP + \\cfrac{FN + FP}{2}}$
它会给予精度和召回率中的低值更高的权重。只有当精度和召回率都很高时， $F_1$ 分数才高。

在 Scikit-Learn 中可以使用 f1_score 来计算 $F_1$ 分数。

from sklearn.metrics import f1_score

f1_score(y_train_5, y_train_pred)
# cm[1, 1] / (cm[1, 1] + (cm[1, 0] + cm[0, 1]) / 2)

0.7325171197343846

$F_1$ 分数对那些具有相近精度和召回率的分类器更有利。在实际情况下，我们有时更关注的是精度，如青少年视频筛选，我们要尽量保证筛选出来的都是符合要求的，而对于财务造假，我们就需要更关注召回率。鱼和熊掌不可兼得，精度和召回率同样也是。

3.5 精度/召回率权衡

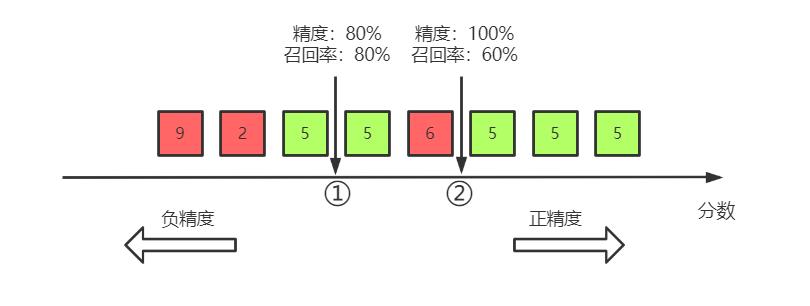
要理解这个权衡过程，首先要知道 SGDClassifier 如何进行分类的。对于数据集中的每一个实例，它会基于决策函数计算出一个分值，如果该值大于设定的阈值，则将该实例判为正类，否则便将其判为负类。
图中显示从左边最低分到右边最高分的几个数字，假设当前决策阈值位于①箭头的位置，在阈值的右边有四个 5（真正类）和一个 6 （假正类），因此精度为 80% 。在五个 5 中，只预测出了 4 个，召回率为 80% 。
现在提高阈值，以②箭头的位置作为决策阈值，此时，精度变为 100% ，召回率变为 60% 。
在这里插入图片描述

Scikit-Learn 不允许直接设置阈值，但可以使用 decision_function() 方法访问它用于预测的决策分数，该方法返回每个实例的分数，根据这些分数就可以使用任意阈值进行预测。下面先获取 3 个实例的决策分数。

y_scores = sgd_clf.decision_function(X[:3])
y_scores

array([ 2164.22030239, -5897.37359354, -13489.14805779])

使用 SGDClassifier 默认的决策阈值 0 ，来得到分类结果。

threshold = 0
y_some_digit_pred = (y_scores > threshold)
y_some_digit_pred

array([ True, False, False])

现在提升阈值看看是否会改变分类结果。

threshold = 3000
y_some_digit_pred = (y_scores > threshold)
y_some_digit_pred

array([False, False, False])

结果发生了改变，这证明提高阈值确实可以降低召回率。

那我们如何在众多的实例中选择恰当的决策阈值？
首先使用 cross_val_predict() 函数获取训练集中所有所有实例的决策分数（修改 method 参数）。

y_scores = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3,
                             method="decision_function")
y_scores.shape

(60000,)

使用 precision_recall_curve() 函数来计算所有可能的阈值的精度和召回率。

from sklearn.metrics import precision_recall_curve

precisions, recalls, thresholds = precision_recall_curve(y_train_5, y_scores)

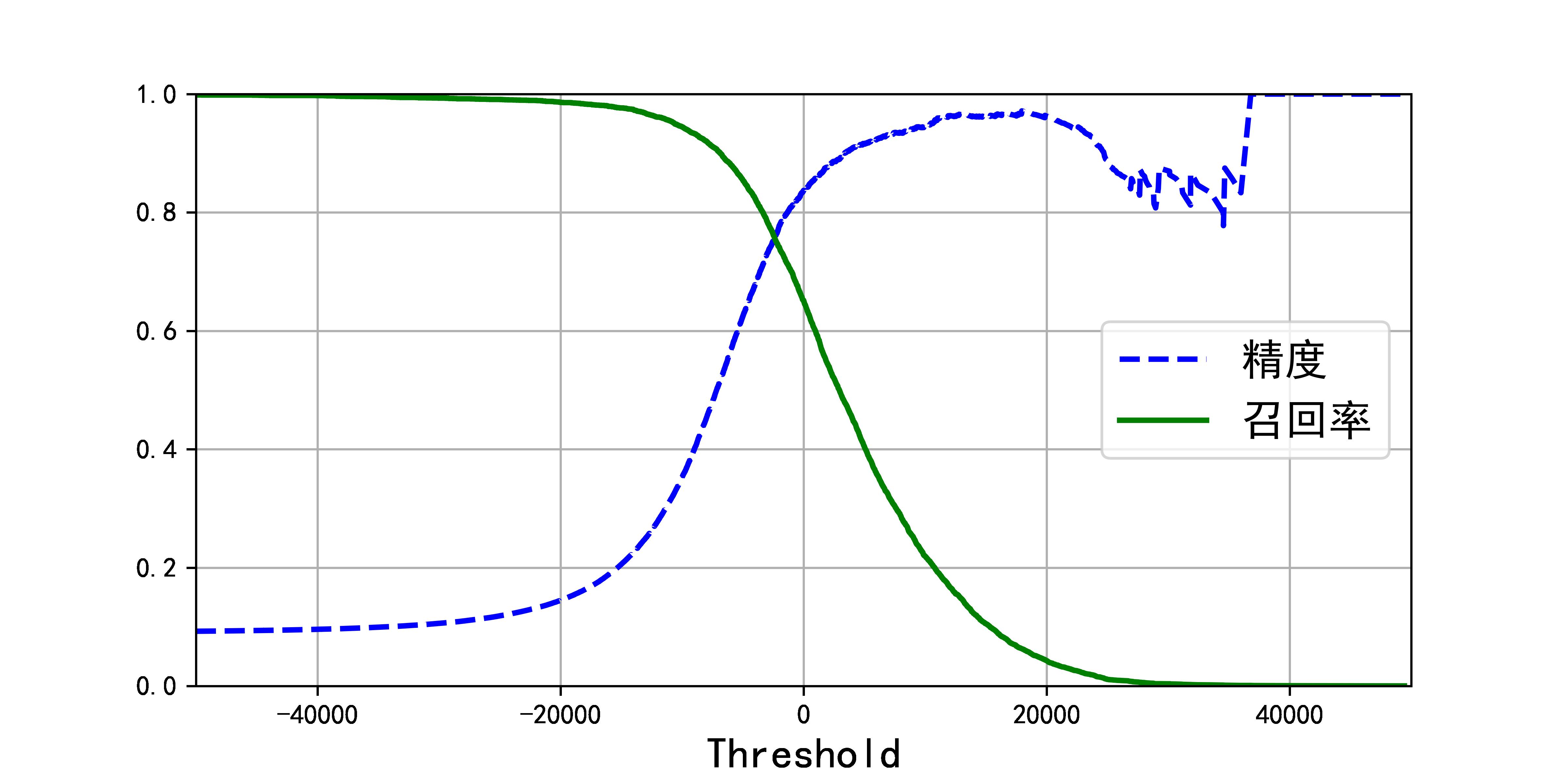
最后使用 Matplotlib 绘制精度和召回率相对于阈值的函数图。

# 显示中文
plt.rcParams['font.family'] = 'SimHei'
# 显示中文负号
plt.rcParams['axes.unicode_minus'] = False

def plot_precision_recall_vs_threshold(precisions, recalls, thresholds):
	# 绘制精度曲线
    plt.plot(thresholds, precisions[:-1], "b--", label="精度", linewidth=2)
    # 绘制召回率曲线
    plt.plot(thresholds, recalls[:-1], "g-", label="召回率", linewidth=2)
    # 设置图例的位置与大小
    plt.legend(loc="center right", fontsize=16)
    # 设置x轴的信息
    plt.xlabel("Threshold", fontsize=16)
    # 显示网格
    plt.grid(True)
    # 指定坐标轴的范围
    plt.axis([-50000, 50000, 0, 1])

# 设置图像的大小
plt.figure(figsize=(8, 4))
plot_precision_recall_vs_threshold(precisions, recalls, thresholds)
# 保存图片
plt.savefig(Path(current_path, "./images/precision_recall_vs_threshold_plot.png"), dpi=600)
plt.show()

注意： 在精度曲线上，上端有部分是崎岖的，这是由于当你提高阈值时，精度有时也可能会下降。

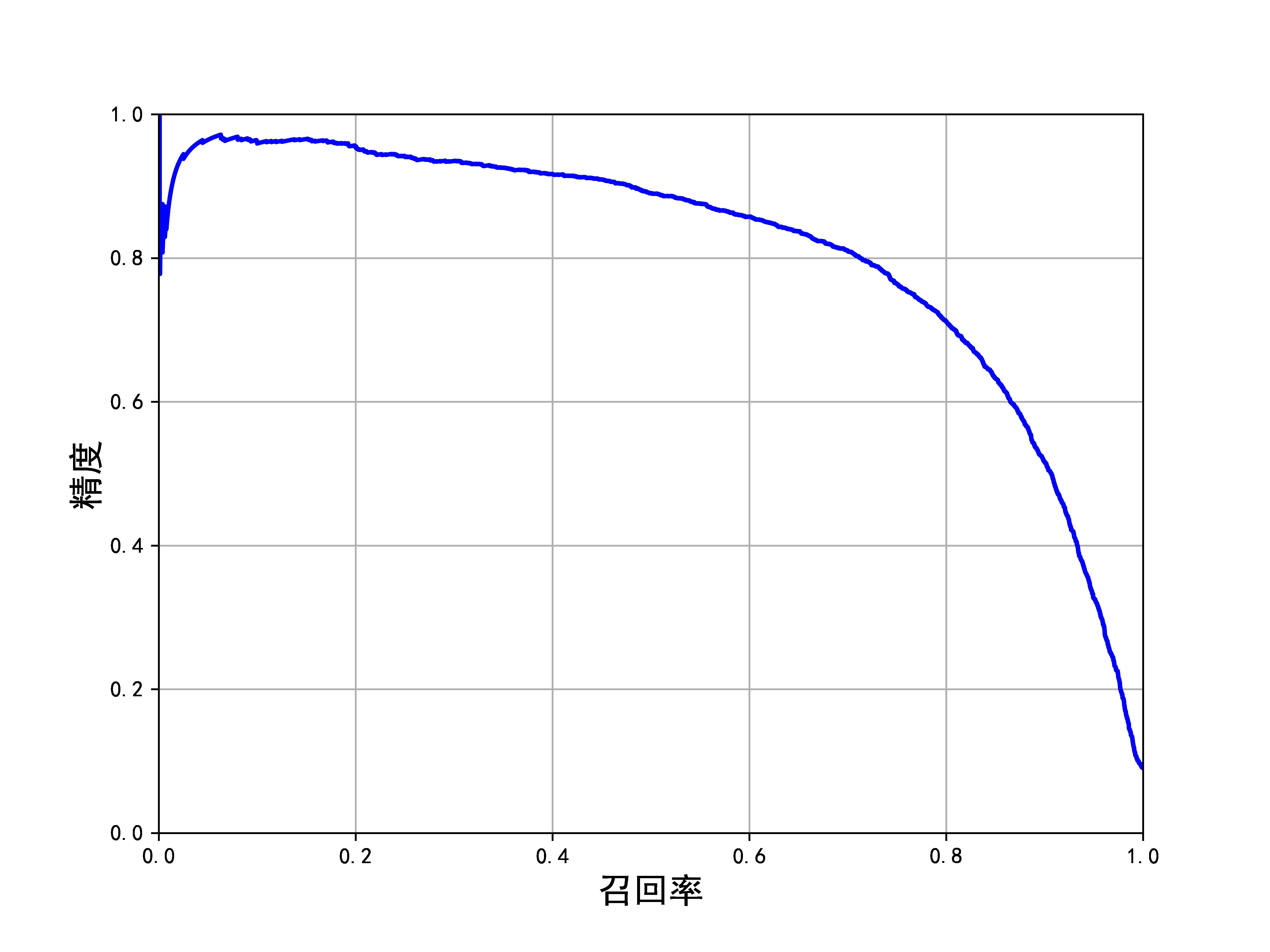
另一种找到好的精度/召回率权衡的方法是直接绘制精度和召回率的函数图。

def plot_precision_vs_recall(precisions, recalls):
    plt.plot(recalls, precisions, "b-", linewidth=2)
    plt.xlabel("召回率", fontsize=16)
    plt.ylabel("精度", fontsize=16)
    plt.axis([0, 1, 0, 1])
    plt.grid(True)

# 设置绘制图像大小
plt.figure(figsize=(8, 6))
# 图像绘制
plot_precision_vs_recall(precisions, recalls)
# 保存图片
plt.savefig(Path(current_path, "./images/precision_vs_recall_plot.png"), dpi=600)
plt.show()