README2动态规划之斐波那契数列说明重叠子问题如何解决

Posted 2021-05-20 快乐江湖

接上文：【README1】动态规划之解题思路

文章目录

• 斐波那契数列讲解——解决重叠子问题
• • （1）暴力递归
  • （2）带有备忘录的递归解法
  • （3）自底向上——dp数组解法
  • （4）总结：状态转移方程
  • （5）状态压缩

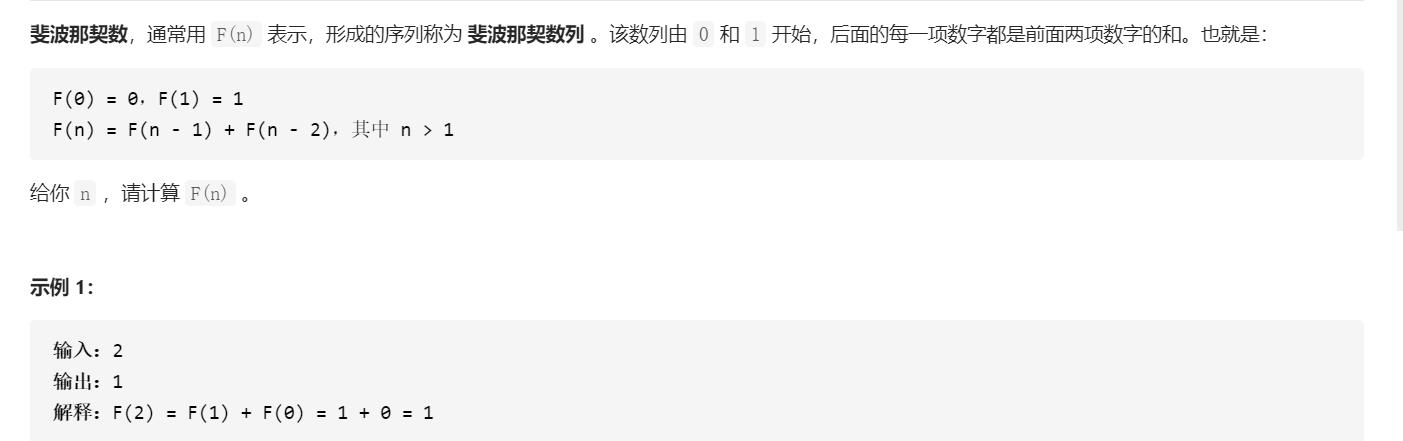
斐波那契数列讲解——解决重叠子问题

所有的理论都需要实际的题目来验证，这里我们不选那些经典的动态规划的题目，因为我们只求抓住最本质，把这个思路讲解清楚，而斐波那契数列就是这样一个很好的例子，当然它并不算是一个非常典型的动态规划的题目。

LeetCode 509：斐波那契数列

接下来，我们会用各个方面来阐述，从时间复杂度最高的递归，再到备忘录和dp数组的解决，逐步讲解动态规划中我们应该怎么去想和怎么优化

（1）暴力递归

斐波那契数列是一个典型的递归题目，它的写法非常简单，这里我就不多强调了

class Solution {
public:
    int fib(int n) 
    {
        if (n==0) return 0;
        if (n==1 || n==2) return 1;
        return fib(n-1)+fib(n-2);
    }
};

题目可以通过，但是时间高的吓人

为什么这么慢呢？其实这就是动态规划的第一个大的问题——重叠子问题

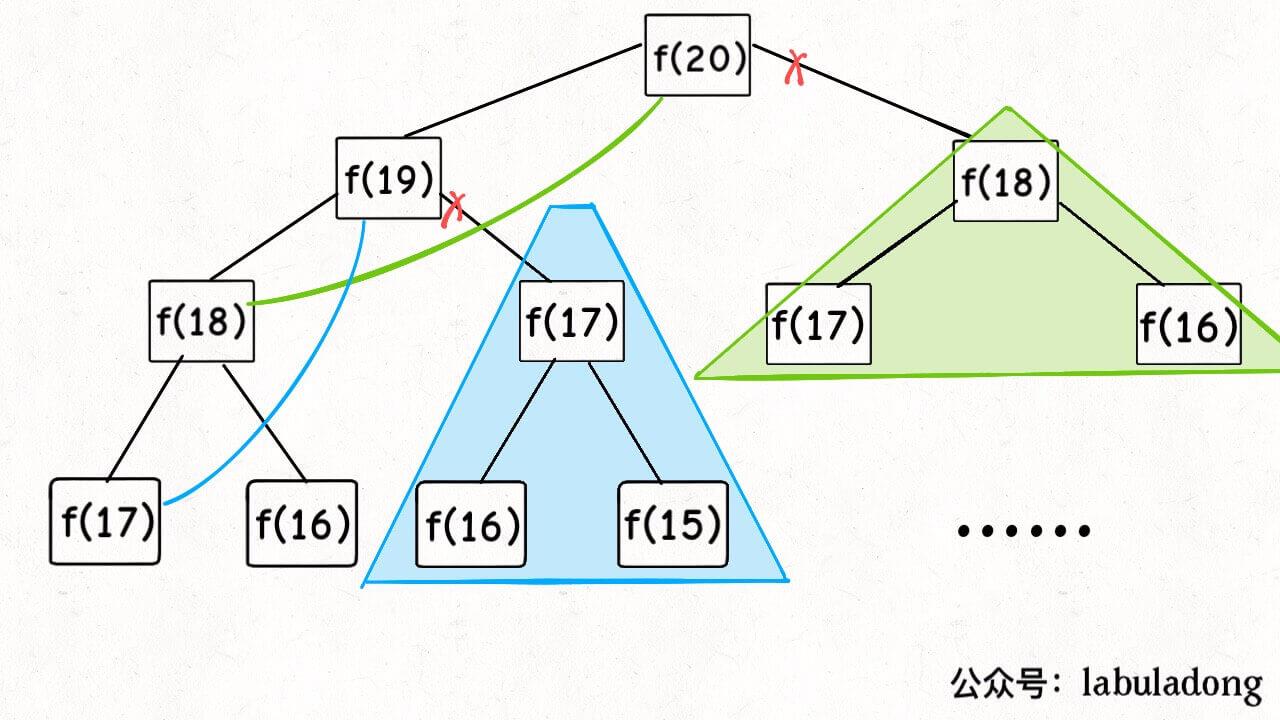
我们知道递归问题本质就是二叉树的问题，所以在递归的过程中就是在遍历一颗二叉树，所以这种接法对应的递归树是这样的

很显然，想要计算fib(20)，就先要计算fib(19)和fib(18)，计算fib(19)又要计算fib(18)和fib(17)…可以看出图中的f(18),f(17)很显然是不需要计算的，虽然图中只画出了一点，但是你应该明白，这颗递归树要是完全展开，那是很恐怖的。所以这个算法极其低效

（2）带有备忘录的递归解法

既然耗时的原因是因为重叠子问题太多，那么不如这样：把fib(18)计算完之后，存储在一个备忘录中，下次只要需要求解fib(18)，直接从备忘录里面拿多好。
而实现备忘录，我们更多用数组，当然你也可以用哈希表，道理是一样的。

class Solution {
public:
    int back(vector<int>& memory,int n)
    {
        if(n==1 || n==2) return 1;
        if(memory[n]!=0) return memory[n];//一旦对应位置不等于0，表示已经计算过了，立马直接返回结果即可

        return back(memory,n-1)+back(memory,n-2);

    }

    int fib(int n) 
    {
        if (n==0) return 0;
        vector<int> memory(n+1,0);//设立一个备忘录，初始状态设置为0，0表示该位置的元素没有被记录在备忘录上
        return back(memory,n);
    }
};

继续观察这种算法的递归树，如下，你可以很明显的发现，这种带备忘录的解法就是我们经常说的“剪枝”操作，以下把一颗非常冗余的树修剪的很干净，或者说就是减少了重叠子问题

如下，很明显它的时间复杂度要低

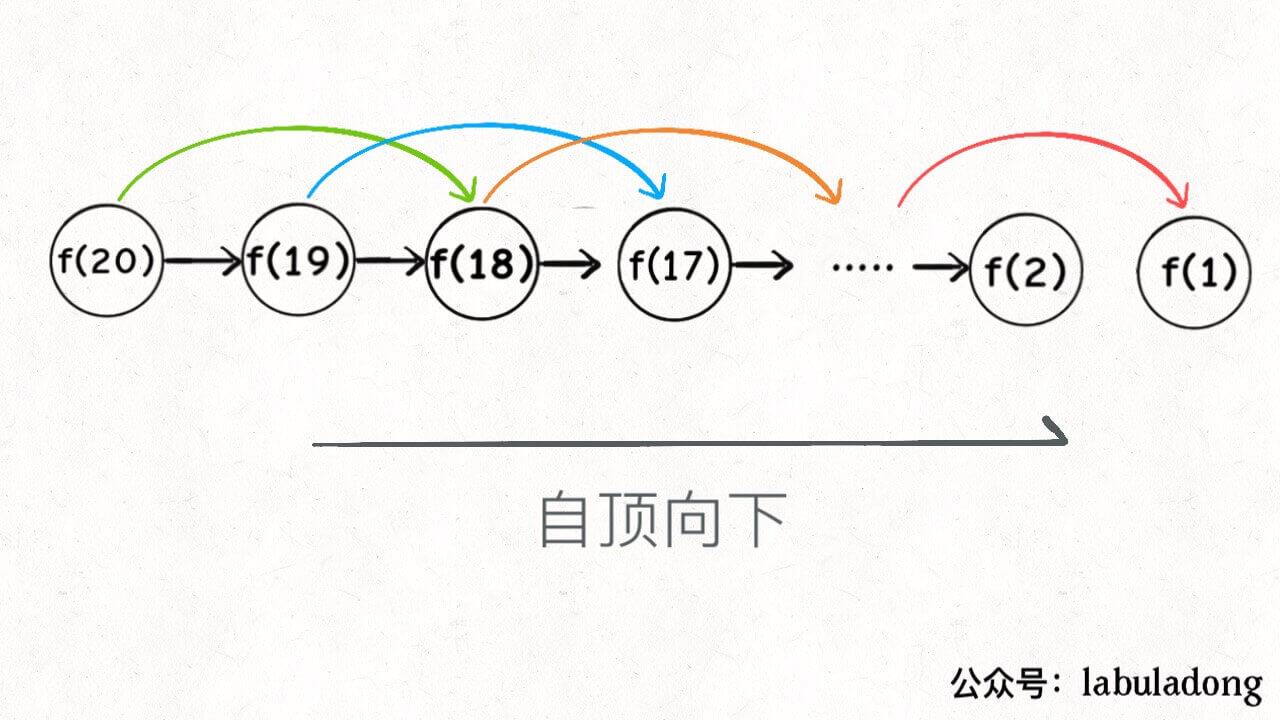
至此，这种算法的效率已经能符合动态规划相应的题目的效率要求了。但是我们现在的解决时自顶向下，而一般的动态规划的题目时自底向上的。

• 自顶向下：从一个原始的问题，也就是规模较大的问题，比如说fib(20)，逐步向下分解，分解到很小的规模,一直分解到再不能分解为止，比如fib(1)和fib(2)这两个base case
• 自底向上：反过来，从最下面，最简单的情况如上，进行反推得到结果。我们动态规划就是按照这种思路来的

（3）自底向上——dp数组解法

我们把上面的备忘录变成一个dp数组，通过dp数组不断迭代向上求解。

class Solution {
public:
    int fib(int n) 
    {
        if(n==0) return 0;
        if(n==1 || n==2) return 1;
        vector<int> dp(n+1,0);

        //最简单的情况，base case
        dp[1]=1;
        dp[2]=1;
        for(int i=3;i<=n;i++)
        {
            dp[i]=dp[i-1]+dp[i-2];
        }

        return dp[n];
    }
};

你会很明显发现，这样的结局效率非常的高

同时这种算法对应的图和带备忘录的递归算法的那张图结果相反

（4）总结：状态转移方程

其实在这个过程中，我们已经不知不觉的使用了状态转移方程。如下，

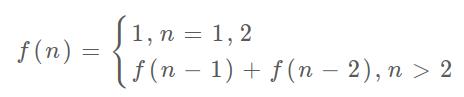
你可以把f(n)当作一个状态，而这个状态n是由状态n-1和状态n-2进行相加操作转移过来的，仅此而已。所以代码中的dp[i]=dp[i-1]+dp[i-2]就是这个意思

那么如何得出状态转移方程呢？其实完全依赖的就是咋们的暴力解法，暴力解法代表的就是状态转移方程，一旦动态规划的题目中你能写出暴力解法，那么剩余的操作无非就是备忘录或dp数组优化了。也就是先自顶向下，再自底向上

（5）状态压缩

至此我们已经解决了重叠子问题，关于如何解决最优子结构会在下篇文章中说明。
对于刚才的例子，还能继续进行优化，就是优化空间，因为在这个斐波那契数列中，当前状态仅仅和前两个状态有关，而前面无关，所以我们可以优化空间，不采用数组，直接两个变量，交替保存。

class Solution {
public:
    int fib(int n) 
    {
        if (n==0) return 0;
        if (n==1 || n==2) return 1;
        int prev=1;int curr=1;
        for(int i=3;i<=n;i++)
        {
            int sum=prev+curr;
            prev=curr;
            curr=sum;
        }
        return curr;
    }
};

所以如果我们发现每次状态转移的时候只需要dp数组中的一部分，那么就可以尝试采用状态压缩来压缩dp table的大小，只记录必要的数据