README3动态规划之“找零钱”说明最优子结构怎么解决

Posted 2021-05-20 快乐江湖

接上文：【README2】动态规划之斐波那契数列说明重叠子问题如何解决

文章目录

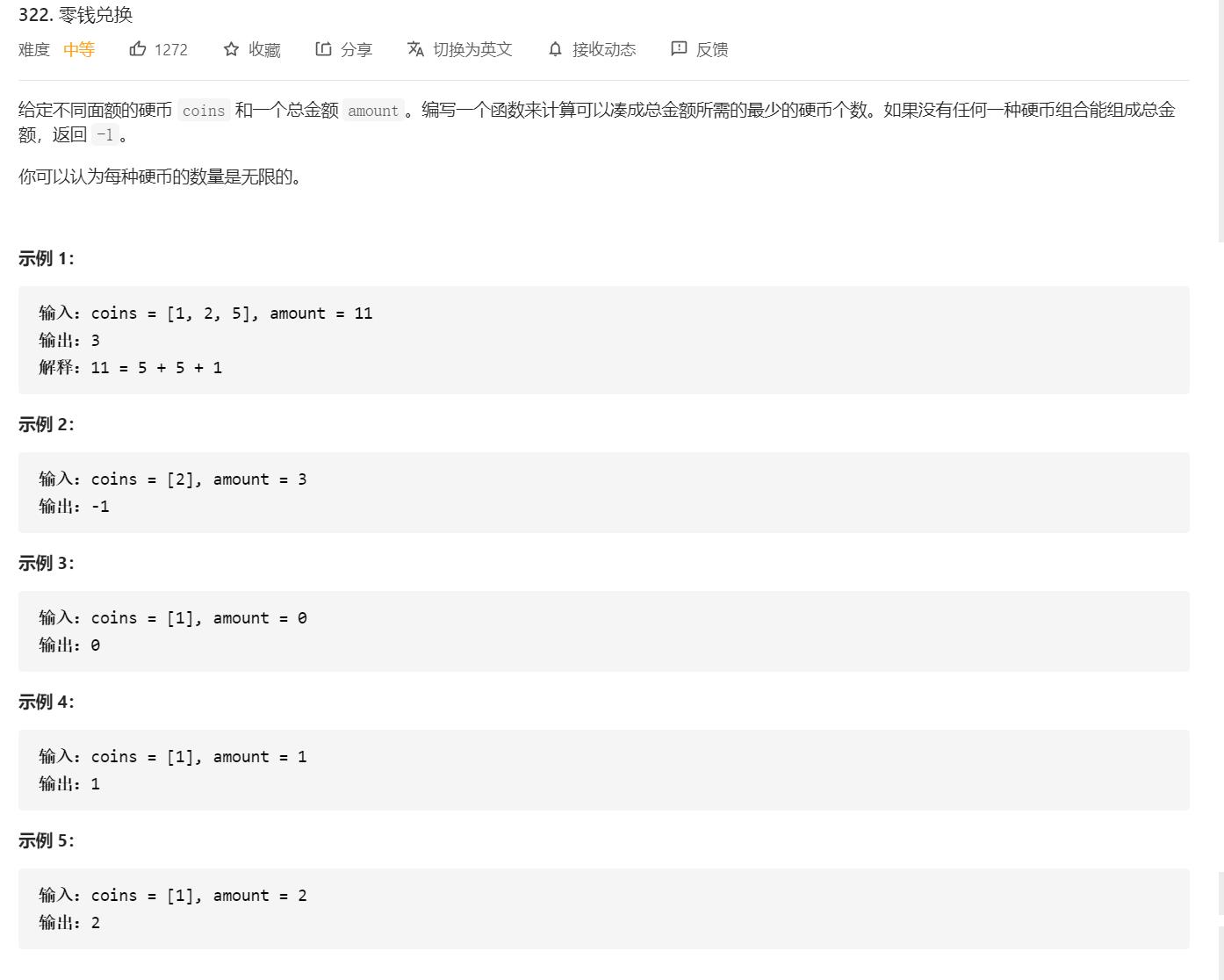
• 找零钱问题说明最优子结构
• • （1）何为最优子结构
  • （2）状态转移方程 暴力解法
  • （3）备忘录解决重叠子问题
  • （4）迭代解法

找零钱问题说明最优子结构

lLeetCode 509：零钱兑换

（1）何为最优子结构

这里面的子结构其实指的就是子问题，但是要成为最优子结构必须满足子问题之间相互独立

举个例子：如果你的终极问题是考的最高的成绩，那么你的子问题就是如何把数学考的最高分，如何把语文考到最高分…这里很明显可以发现，数学和语文以及其他科目的成绩不会相互制约，所以这个过程符合最优子结构。一旦子问题之间相互干扰，比如数学考的越高，语文考的越低，那么永远也无法得到最高分，这就不是最优子结构

回到凑零钱的问题来，它就很好的满足了最优子结构。以下面这个例子为例

你想要解决“如何以最少的硬币凑够11元”的问题，那么那就需要先解决“如何以最少的硬币凑够10元”的子问题，因为一旦满足刚才的子问题，只需要加上一块硬币（面值为1）就能解决终极问题了。

（2）状态转移方程 暴力解法

前文就说过，暴力解法本质体现的就是状态转移方程，一旦能够列出状态转移方程，剩余的只是一些比较容易的优化工作

所以这里我们按照之前列状态转移方程的思路，进行探求

1. base case（最简单的情况）是什么：很显然使目标金额如果为0，就让程序返回0，此时不需要任何硬币就可以凑出目标金额了
2. 这个问题有什么状态？也即是原问题和子问题的变量：也很简单，金额数是在不断变化的，不断向base case靠近。
3. 每个状态可以做怎样得到选择使得状态变化：这也很清晰，每次进入递归时可以选择一个面值的硬币，相当于减少了目标金额数
4. 如何定义dp数组或递归函数来表达状态和选择：见下

我们说过暴力解法实则就是自顶向下的过程，所以这里定义的dp函数的参数一般就是状态转移中的变量，函数的返回值则是题目让我们求的值
就这道题而言，能很明确金额数可以作为函数形参，返回值就是要求的硬币的数量

根据以上思路，写出算法的伪代码

def coinChange(coins:List[int],amout:int)
{
	#定义：要凑出金额n，至少需要dp[n]枚硬币
	def dp[n]:
		#做选择，选择需要硬币最少的那个结果
			for coin in coins
				res=min(res,1+dp[n-coin])
			return res
	#题目最终要求的结果是amount
	return dp[amount];
}

如下，根据伪代码我们可以写出暴力解法的代码

class Solution {
public:
    int dp(vector<int>& coins,int n)
    {
        if (n==0) return 0;
        if (n<0) return -1;//base case
        int res=INT_MAX;//INT_MAX代表永远都取不到，
        for(size_t i=0;i<coins.size();i++)
        {
            int subproblem=dp(coins,n-coins[i]);//状态变化，选择了一块硬币，金额就变少了
            if(subproblem==-1)//如果等于-1表明行不通，继续下一个
                continue;
            res=min(res,1+subproblem);//始终保持最小
        }
        if (res!=INT_MAX)//永远都取不到就会返回-1
            return res;
        else
            return -1;
        
    }
    
    int coinChange(vector<int>& coins, int amount) 
    {
       return dp(coins,amount);
        
    }
};

暴力解法就代表了状态转移方程，所以它的状态转移方程为

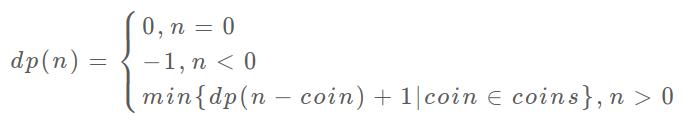
当然这道题是无法通过的，因为暴力解法时间复杂度太大

画出递归树，就可以看见很多重叠子问题没有解决

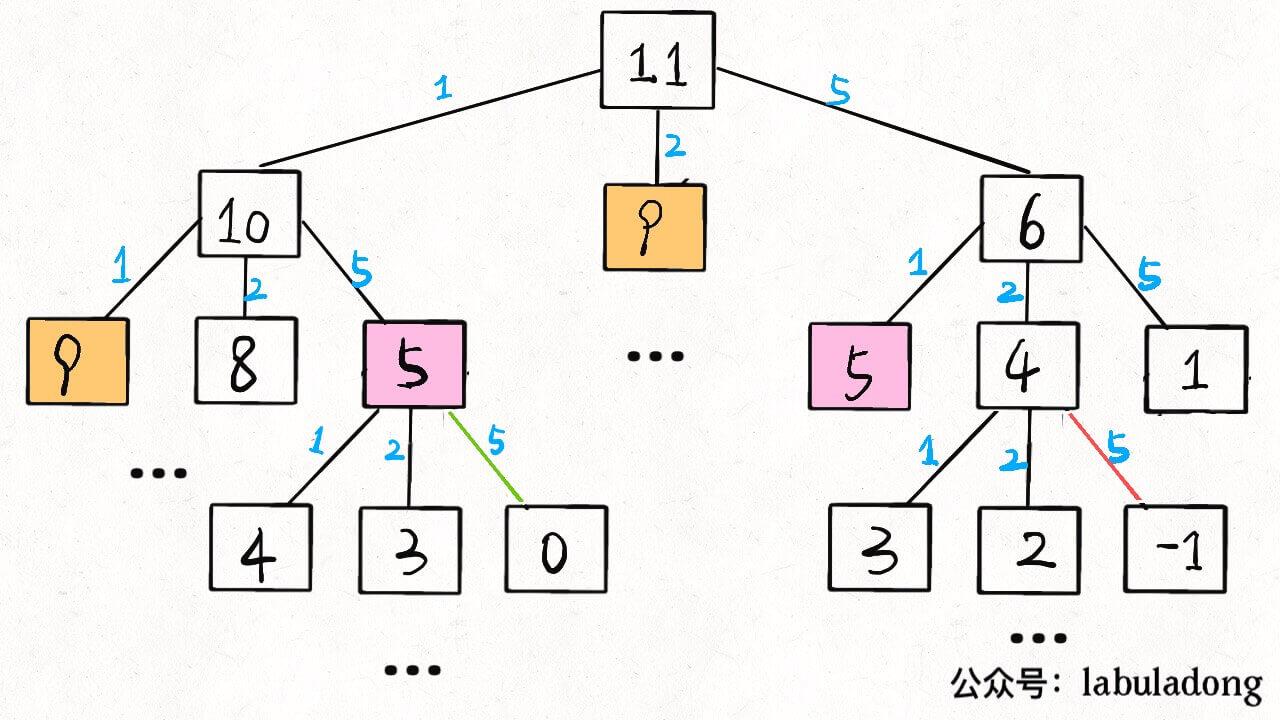
（3）备忘录解决重叠子问题

所以为了降低时间复杂度，我们设置一个备忘录，如果有值就直接拿取

class Solution {
public:
    int dp(vector<int>& coins,int n,unordered_map<int,int>& memory)
    {
        //每次进入dp后首先查备忘录
        if(memory.find(n)!=memory.end())
            return memory[n];
        if (n==0) return 0;
        if (n<0) return -1;//base case        
        
        int res=INT_MAX;
        for(size_t i=0;i<coins.size();i++)
        {
            int subproblem=dp(coins,n-coins[i],memory);
            if(subproblem==-1)
                continue;
            res=min(res,1+subproblem);
            memory[n]=res;//加入备忘录
        }
        if (res!=INT_MAX)
        {
            return memory[n];
        }
        else
            return -1;
        
    }
    
    int coinChange(vector<int>& coins, int amount) 
    {
       unordered_map<int,int> memory;
       return dp(coins,amount,memory);
        
    }
};

（4）迭代解法

如果采用迭代解法解决，则和前面的有所区别，前面的dp函数中，参数列表是状态，返回值是目标值。如果采用迭代写法，那么索引就是状态，索引对应的数组值就是返回结果

class Solution {
public:
    int coinChange(vector<int>& coins, int amount) 
    {
        //amount金额的硬币最多需要amount块硬币（全为1，初始化amount+1相当于是正无穷，方面后续取最小值）
        vector<int> dp(amount+1,amount+1);
        dp[0]=0;//base case
        
        
        for(int i=0 ;i < dp.size();i++)//最外层的for循环遍历的是每个状态
        {
            for(auto coin : coins)//该for循环用于求所有选择的最小值
            {
                if(i-coin<0)//子问题无解
                    continue;
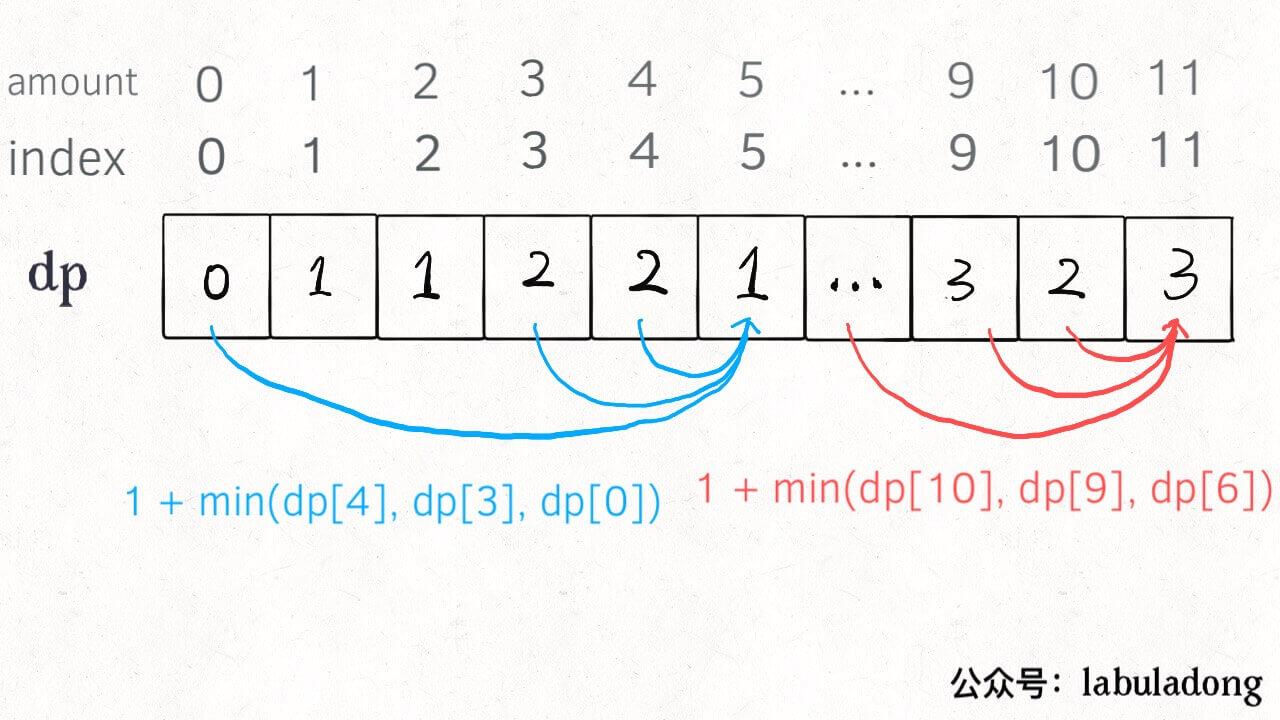
                dp[i]=min(dp[i],1+dp[i-coin]);//状态转移，想象11和10的关系
            }
        }
        
        return (dp[amount]==amount+1) ? -1 : dp[amount];
    }
};