《MonoDepth2:Digging Into Self-Supervised Monocular Depth Estimation》论文笔记
Posted m_buddy
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了《MonoDepth2:Digging Into Self-Supervised Monocular Depth Estimation》论文笔记相关的知识,希望对你有一定的参考价值。
参考代码:monodepth2
1. 概述
导读:由于图片的准确深度信息获取的代价是比较大的,因而使用带有标注的数据去训练会存在较大的成本。因此近来自监督的方法吸引了较多研究者的注意,本篇文章研究的是单目下的自监督深度估计问题,基于经典的计算机视觉原理,文章将深度估计任务划分为两个互补子功能模块:
1)从目标图像(target image)通过编解码网络预测深度信息;
2)从源图像(source images)和目标图像组成的图像对中去估计出该图像对之间的变换关系(由旋转和平移组成的6维度变换状态);
为了更近一步提升深度估计的性能,文章还提出了更具实际意义的损失函数及策略:
1)使用最小重构误差损失作为最后的损失函数,增加对于视频序列中存在遮挡情况的鲁棒性,以及解决平均重构误差损失带来的模糊问题;
2)使用多尺度预测(统一resize在训练图分辨率上)并计算损失,不仅避免了陷入局部最优,而且使得深度的监督输入图片分辨率下更有指向性,从而减少视觉伪影的产生;
3)使用auto-mask策略去排除违反相机运动假设的像素(像素位置相对静止/低纹理区域等),避免了无关像素的干扰,从而提升训练的鲁棒性;
文章的终极目标是从单张图像里面去估计出深度信息,现有的一些自监督的方法已经可以通过立体图像对和单目视频完成训练。对于单目视频的训练由于没有立体视觉系统的先验信息,因而它需要一个额外的姿态估计网络(文中估计6个维度的变化),从而构建一个可行的自监督深度估计方案。对于立体视觉系统是通过离线的方式完成标定,因而不需要姿态估计网络但是其在遮挡和texture-copy artifacts存在问题(那么借鉴文章中提到的策略那么是不是可以反向提升立体视觉的性能呢?doge…)。
整体上文章的方法清晰,使用的策略也很得当,最后生成的结果与其它一些方法的对比见下图所示:
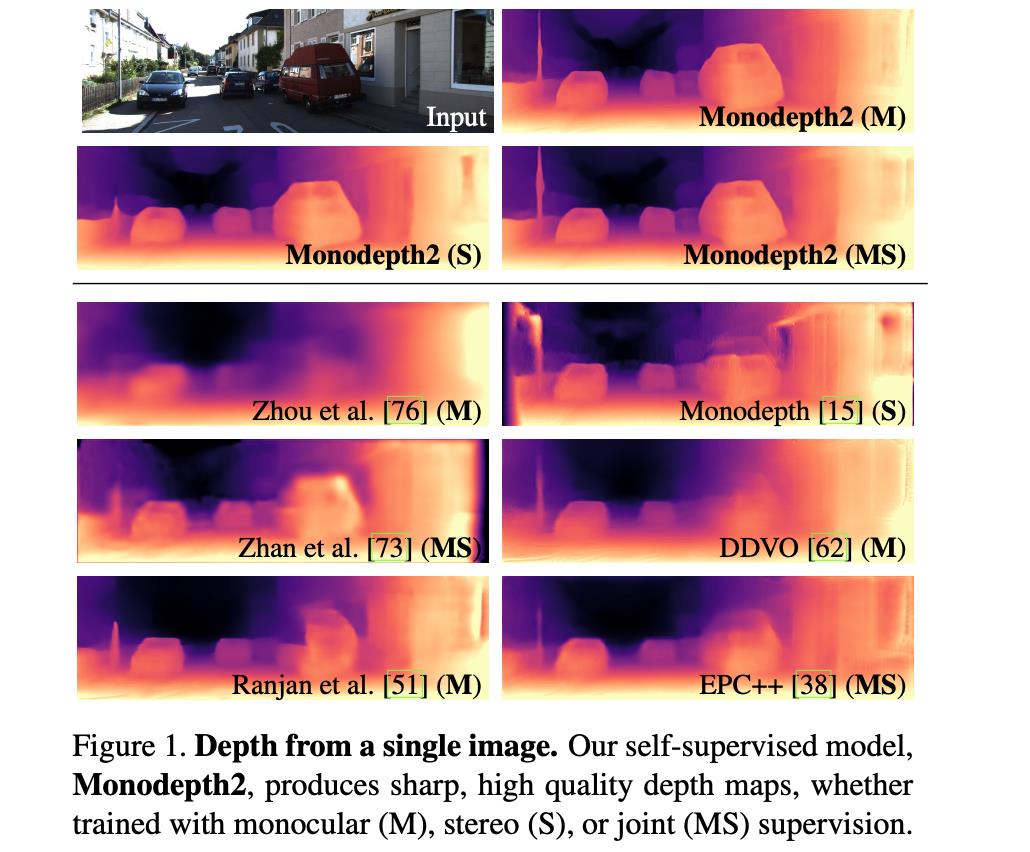
2. 方法设计
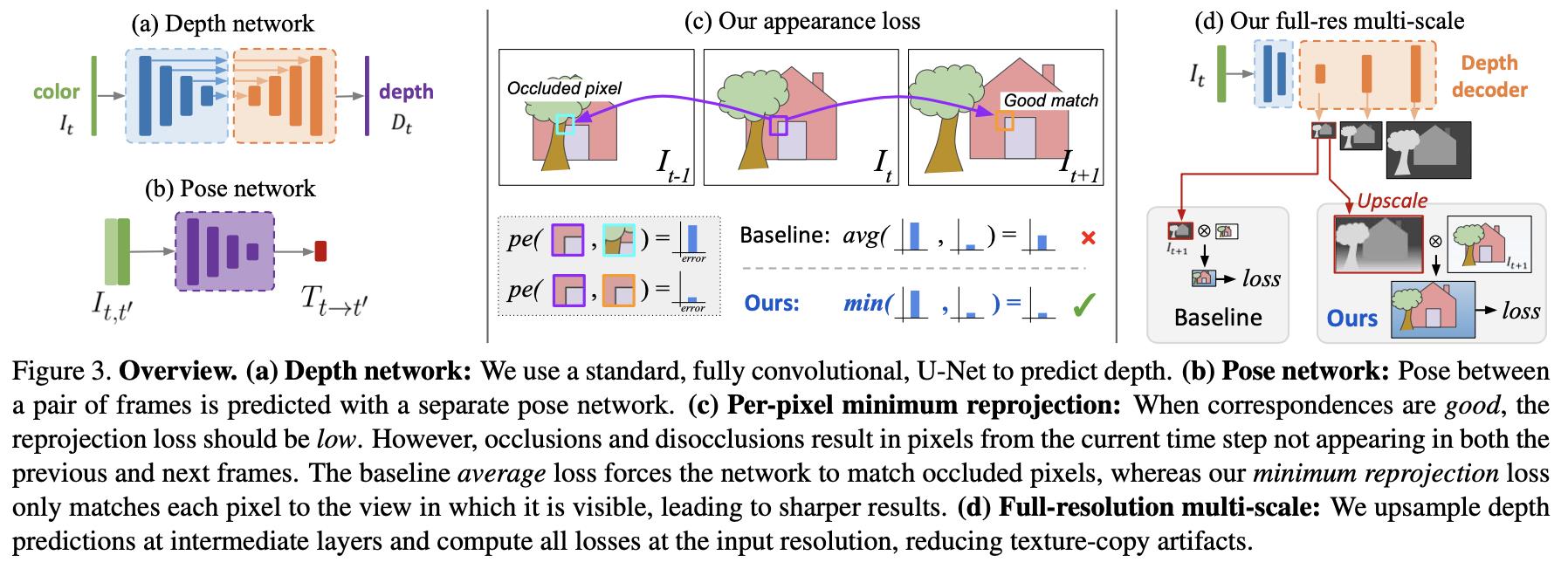
2.1 网络结构
文章方法整体的网络结构由两部分组成:U型结构构建的物体深度信息编解码单元和视频帧对作为输入的姿态估计单元,见图3的(a)(b)图所示。
2.2 自监督训练
这里将当前需要估计的视频帧(测试的时候输入单张图片即可)为目标图像,记为 I t I_t It。对应的前后帧为源图像,记为 I t ‘ = { I t − 1 , I t + 1 } I_{t^{‘}}=\\{I_{t-1},I_{t+1}\\} It‘={It−1,It+1}(在使用立体视觉系统的时候其为另外一个摄像头的数据)。其在训练时只使用单目视频那么生成的模型标号为M(monocular),若是立体视频数据训练的则记为S(stereo),若是混合训练的记为MS。
那么文章的方法就是需要从源图像出发根据估计出来的深度信息和姿态信息重建出目标图像,整个优化的过程就是要最小化重建误差。这里将重建误差表示为:
L
p
=
∑
t
‘
p
e
(
I
t
,
I
t
‘
→
t
)
L_p=\\sum_{t^{‘}}pe(I_t,I_{t^{‘}\\rightarrow t})
Lp=t‘∑pe(It,It‘→t)
其中,从源图像到目标图像的映射过程描述为:
I
t
‘
→
t
=
I
t
‘
⟨
p
r
o
j
(
D
t
,
T
t
→
t
‘
,
K
)
⟩
I_{t^{‘}\\rightarrow t}=I_{t^{‘}}\\langle{proj(D_t,T_{t\\rightarrow t^{‘}},K)}\\rangle
It‘→t=It‘⟨proj(Dt,Tt→t‘,K)⟩
这里的重构误差
p
e
pe
pe使用的是
L
1
L_1
L1损失函数。
p
r
o
j
(
)
proj()
proj()代表的是按照给定的参数进行映射之后的坐标,
D
t
D_t
Dt是估计出来的深度信息,
T
t
→
t
‘
T_{t\\rightarrow t^{‘}}
Tt→t‘是姿态信息,
K
K
K是相机的内部参数。
⟨
⟩
\\langle\\rangle
⟨⟩是采样的策略,这与后面讲到的auto-mask等策略相关。
其中具体两个图像之间的重建误差被描述为:
p
e
(
I
a
,
I
b
)
=
α
2
(
1
−
S
S
I
M
(
I
a
,
I
b
)
)
+
(
1
−
α
)
∣
∣
I
a
−
I
b
∣
∣
1
pe(I_a,I_b)=\\frac{\\alpha}{2}(1-SSIM(I_a,I_b))+(1-\\alpha)||I_a-I_b||_1
pe(Ia,Ib)=2α(1−SSIM(Ia,Ib))+(1−α)∣∣Ia−Ib∣∣1
其中,将上式中的平衡因子设置为
α
=
0.85
\\alpha=0.85
α=0.85。此外为了增加边界的平滑性,引入损失函数:
L
s
=
∣
∂
x
d
t
∗
∣
e
−
∣
∂
x
I
t
∣
+
∣
∂
y
d
t
∗
∣
e
∂
y
I
t
L_s=|\\partial_xd_t^{*}|e^{-|\\partial_xI_t|}+|\\partial_yd_t^{*}|e^{\\partial_yI_t}
Ls=∣∂xdt∗∣e−∣∂xIt∣+∣∂ydt∗∣e∂yIt
其中,
d
t
∗
=
d
t
d
t
ˉ
d_t^{*}=\\frac{d_t}{\\bar{d_t}}
dt∗=dtˉdt是将深度信息进行均值归一化,避免深度的消散。
2.2 自监督训练中的策略
像素的最小重建误差:
在之前的一些方法中使用源图像中的所有像素的重构误差取平均(这里说的重建也就是对应世界坐标和图像坐标之间的变换)。但是这样的方式在视频序列存在如下问题的时候损失就会变得很大(见图3(c)所示),从而造成训练过程的不稳定:
- 1)由于如相机运动而导致一些像素移出了图像的边界;
- 2)由于视频中目标移动导致视频中的目标存在遮挡;
此外,使用均值重建误差会导致不同深度过度上模糊。对此文章使用的是对应像素的最小值作为最后的损失函数:
L
p
=
min
t
‘
p
e
(
I
t
,
I
t
‘
→
t
)
L_p=\\min_{t^{‘}}pe(I_t,I_{t^{‘}\\rightarrow t})
Lp=t‘minpe(It,It‘→t)
使用上述的方式可以排除一些异常的点,从而增加训练的鲁棒性,深度边界锐化。下图中展示的是在不同图像对上的匹配情况:

auto-masking策略:
自监督的深度估计数据场景是需要在静态场景下使用运动的相机进行数据采集。若采集视频中的目标存在运动的情况(违反了前期的条件假设)那么就会导致对应的区域存在“孔洞”,见下图所示:
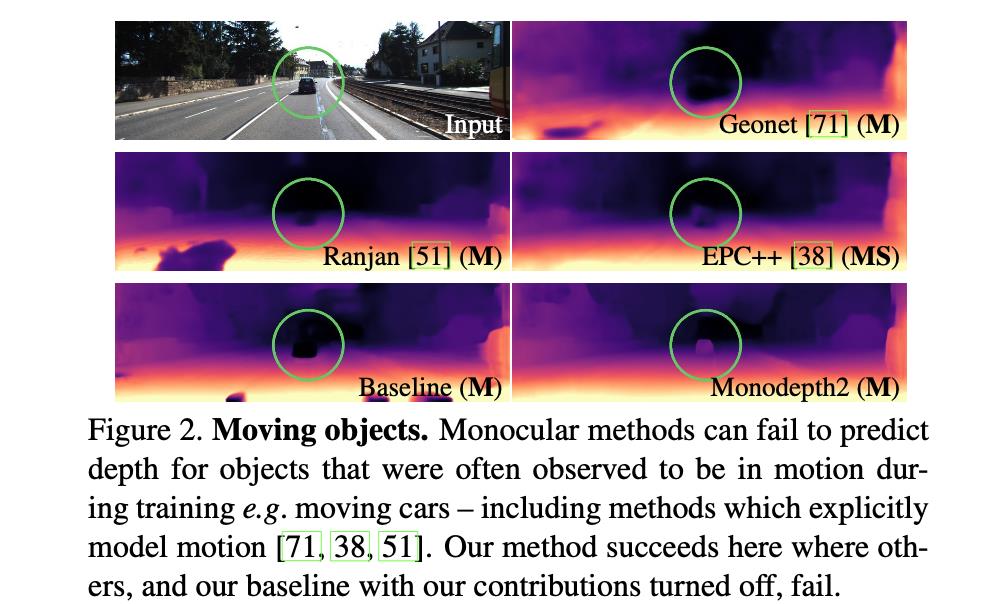
对此文章引入auto-masking策略去排除那些帧间静止的像素/低纹理区域/与相机运动相对静止的像素。文章使用
μ
∈
{
0
,
1
}
\\mu\\in\\{0,1\\}
μ∈{0,1}掩膜进行区分,它设置的逻辑是帧间重构误差小于帧间误差,既是表示为:
μ
=
min
t
’
p
e
(
I
t
,
I
t
’
→
t
)
<
min
t
’
p
e
(
I
t
,
I
t
’
)
\\mu=\\min_{t^{’}}pe(I_t,I_{t^{’}\\rightarrow t})\\lt\\min_{t^{’}}pe(I_t,I_{t^{’}})
μ=t’minpe(It,It’→t)<t以上是关于《MonoDepth2:Digging Into Self-Supervised Monocular Depth Estimation》论文笔记的主要内容,如果未能解决你的问题,请参考以下文章