LintCode 440 · 背包问题 III---完全背包问题

Posted 2021-05-20 大忽悠爱忽悠

---

背包问题 III 题解集合

• 动态规划常规解法
• 「滚动数组」解法
• 「一维空间优化」解法

---

动态规划常规解法

有 N 种物品和一个容量为 C 的背包，每种物品都有无限件。

dp[i][j] 代表考虑前 i 件物品，放入一个容量为 j 的背包可以获得的最大价值。

由于每件物品可以被选择多次，因此对于某个 dp[i][j] 而言，其值应该为以下所有可能方案中的最大值：

• 选择 0 件物品 i 的最大价值，即dp[i-1][j]
• 选择 1 件物品 i 的最大价值，即dp[i-1][j-v[i]]+w[i]
• 选择 2 件物品 i 的最大价值，即dp[i-1][j-2*v[i]]+2 * w[i]
• …
• 选择 k 件物品 i 的最大价值，即dp[i-1][j-k* v[i]]+ k*w[i]

由此我们可以得出「状态转移方程」为：

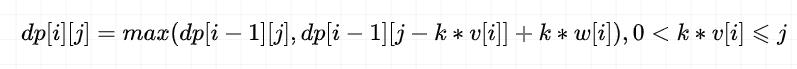
代码：

class Solution {
public:
    int backPackIII(vector<int>& A, vector<int>& V, int m) 
	{
		if (A.empty() || V.empty()) return 0;
		int num = A.size();//物品的个数
		vector<vector<int>> dp(num, vector<int>(m + 1, 0));

		//初始化第一行，即对第一个物品所有状态进行初始化
		for (int i = 0; i <= m; i++)
		{
			// 显然当只有一件物品的时候，在容量允许的情况下，能选多少件就选多少件
			int maxK = i / A[0];
			dp[0][i] = maxK * V[0];
		}

		//处理剩余物品对应的所有状态，也可以理解为处理剩余行
		for (int i = 1; i < num; i++)
		{
			for (int j = 0; j <= m; j++)
			{
				// 不考虑第 i 件物品的情况（选择 0 件物品 i）
				int unsel = dp[i - 1][j];
				// 考虑第 i 件物品的情况,再当前容量j下，塞入多少件物品i,能够获得最大价值
				int sel = 0;//获取最大价值
				for (int k = 1; ; k++)
				{
					//直到剩余容量不能再塞入时，说明考虑完了所有情况
					if (j < A[i] * k)
						break;
					sel = max(sel, dp[i - 1][j - k * A[i]] + k * V[i]);
				}

				dp[i][j] = max(sel, unsel);
			}
		}

		return dp[num - 1][m];
    }
};

---

「滚动数组」解法

通过观察我们的「状态转移方程」可以发现，我们在更新某个 dp[i][x] 的时候只依赖于 dp[i-1][x]。

因此我们可以像 01 背包那样使用「滚动数组」的方式将空间优化到O(C） 。

代码：

class Solution {
public:
    int backPackIII(vector<int>& A, vector<int>& V, int m) 
	{
		if (A.empty() || V.empty()) return 0;
		int num = A.size();//物品的个数
		vector<vector<int>> dp(2, vector<int>(m + 1, 0));

		//初始化第一行，即对第一个物品所有状态进行初始化
		for (int i = 0; i <= m; i++)
		{
			// 显然当只有一件物品的时候，在容量允许的情况下，能选多少件就选多少件
			int maxK = i / A[0];
			dp[0][i] = maxK * V[0];
		}

		//处理剩余物品对应的所有状态，也可以理解为处理剩余行
		for (int i = 1; i < num; i++)
		{
			for (int j = 0; j <= m; j++)
			{
				// 不考虑第 i 件物品的情况（选择 0 件物品 i）
				int unsel = dp[(i - 1)&1][j];
				// 考虑第 i 件物品的情况,再当前容量j下，塞入多少件物品i,能够获得最大价值
				int sel = 0;//获取最大价值
				for (int k = 1; ; k++)
				{
					//直到剩余容量不能再塞入时，说明考虑完了所有情况
					if (j < A[i] * k)
						break;
					sel = max(sel, dp[(i - 1)&1][j - k * A[i]] + k * V[i]);
				}

				dp[i&1][j] = max(sel, unsel);
			}
		}

		return dp[(num - 1)&1][m];
    }
};

---

「一维空间优化」解法

我们知道在 01 背包中，最重要的是「一维空间优化」解法。

之所以 01 背包能够使用「一维空间优化」解法，是因为当我们开始处理第 i 件物品的时候，数组中存储的是已经处理完的第 i-1 件物品的状态值。

然后配合着我们容量维度「从大到小」的遍历顺序，可以确保我们在更新某个状态时，所需要用到的状态值不会被覆盖。

因此 01 背包问题的状态转移方程为：

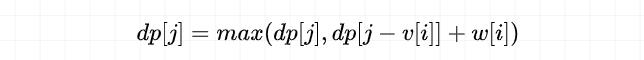
同时容量维度的遍历顺序为从大到小。

PS. 如果你不太理解上面的话，或许是因为你「还没学习」或者「有点忘记」01 背包问题，强烈建议你先对 01 背包问题 进行学习/回顾。

而「完全背包」区别于「01 背包」，在于每件物品可以被选择多次。

因此你可能会在别的地方看到这样的讲解：

「01 背包将容量维度「从大到小」遍历代表每件物品只能选择一件，而完全背包将容量维度「从小到大」遍历代表每件物品可以选择多次。」

这样的解释其实是利用了人的抽象思维，但感觉不一定是对的。

接下来，我们从「数学」的角度去证明为什么修改 01 背包的遍历顺序可以正确求解完全背包问题。

我们先来展开完全背包中 的所有可能方案：



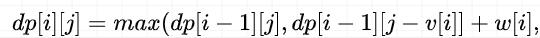
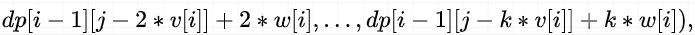
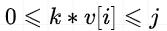
dp[i][j] 所代表的含义：在容量允许的情况下，对于第 i 件物品，我们可以不选，可以选 1 次，可以选 2 次，…，可以选 k 次 …

然后我们通过代入，看看 dp[i][j-v[i]] 是什么内容：



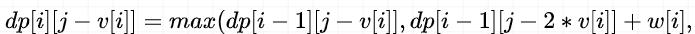
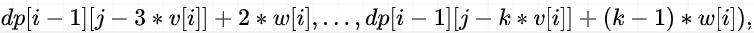
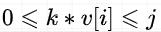
光看公式可能很难看出两者的联系，下面我将相同的部分进行标记：

总结一下。

• 0-1 背包问题的状态转换方程是：
  

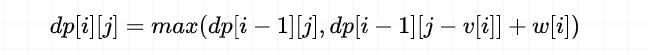
由于计算 dp[i][j] 的时候，依赖于 dp[i-1][j-v[i]]。

因此我们在改为「一维空间优化」时，需要确保 dp[j-v[i]] 存储的是上一行的值，即确保 dp[j-v[i]] 还没有被更新，所以遍历方向是从大到小。

• 完全背包问题的状态转移方程是：
  

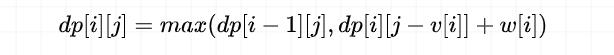
由于计算 dp[i][j] 的时候，依赖于 dp[i][j-v[i]]。

因此我们在改为「一维空间优化」时，需要确保 dp[j-v[i]] 存储的是当前行的值，即确保 dp[j-v[i]] 已经被更新，所以遍历方向是从小到大。

代码：

class Solution {
public:
    int backPackIII(vector<int>& A, vector<int>& V, int m) 
	{
		if (A.empty() || V.empty()) return 0;
		int num = A.size();//物品的个数
		vector<int> dp(m + 1, 0);
		//处理剩余物品对应的所有状态，也可以理解为处理剩余行
		for (int i = 0; i < num; i++)
		{
			for (int j = 0; j <= m; j++)
			{
				// 不考虑第 i 件物品的情况（选择 0 件物品 i）
				int unsel = dp[j];
				// 考虑第 i 件物品的情况
				int sel = j>=A[i]?dp[j-A[i]]+V[i]:0;
                 
				dp[j] = max(sel, unsel);
			}
		}
		return dp[m];
    }
};

另一种写法：

class Solution {
public:
    int backPackIII(vector<int>& A, vector<int>& V, int m) 
	{
		if (A.empty() || V.empty()) return 0;
		int num = A.size();//物品的个数
		vector<int> dp(m + 1, 0);
		//处理剩余物品对应的所有状态，也可以理解为处理剩余行
		for (int i = 0; i < num; i++)
		{
			for (int j = 0; j <= m; j++)
			{
				// 不考虑第 i 件物品的情况（选择 0 件物品 i）
				int unsel = dp[j];
				// 考虑第 i 件物品的情况,再当前容量j下，塞入多少件物品i,能够获得最大价值
				int sel = 0;//获取最大价值
				for (int k = 1; ; k++)
				{
					//直到剩余容量不能再塞入时，说明考虑完了所有情况
					if (j < A[i] * k)
						break;
					sel = max(sel, dp[j - k * A[i]] + k * V[i]);
				}

				dp[j] = max(sel, unsel);
			}
		}
		return dp[m];
    }
};

当然从尾端往前端覆盖的写法也没错

class Solution {
public:
	int backPackIII(vector<int>& A, vector<int>& V, int m)
	{
		if (A.empty() || V.empty()) return 0;
		int num = A.size();//物品的个数
		vector<int> dp(m + 1, 0);
		//处理剩余物品对应的所有状态，也可以理解为处理剩余行
		for (int i = 0; i < num; i++)
		{
			for (int j = m; j>=A[i]; j--)
			{
				// 不考虑第 i 件物品的情况（选择 0 件物品 i）
				int unsel = dp[j];
				// 考虑第 i 件物品的情况,再当前容量j下，塞入多少件物品i,能够获得最大价值
				int sel = 0;//获取最大价值
				for (int k = 1; ; k++)
				{
					//直到剩余容量不能再塞入时，说明考虑完了所有情况
					if (j < A[i] * k)
						break;
					sel = max(sel, dp[j - k * A[i]] + k * V[i]);
				}

				dp[j] = max(sel, unsel);
			}
		}
		return dp[m];
	}
};