通信系统未编码卷积码与格雷码的仿真性能比较

Posted 2021-05-20 踟蹰横渡口,彳亍上滩舟。

通信系统未编码、卷积码与格雷码的仿真性能比较

论文+代码+仿真结果：下载地址

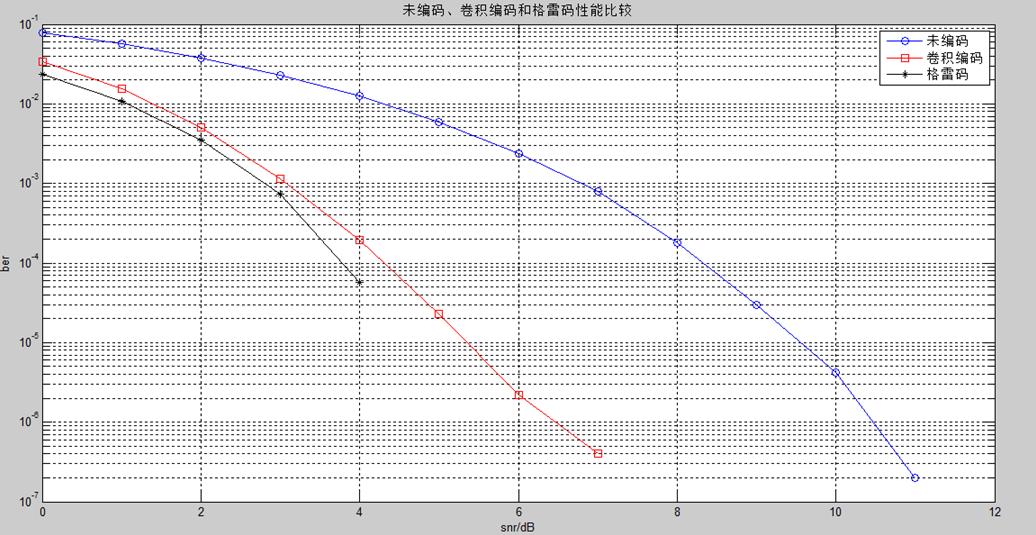
以上仿真结果可知：
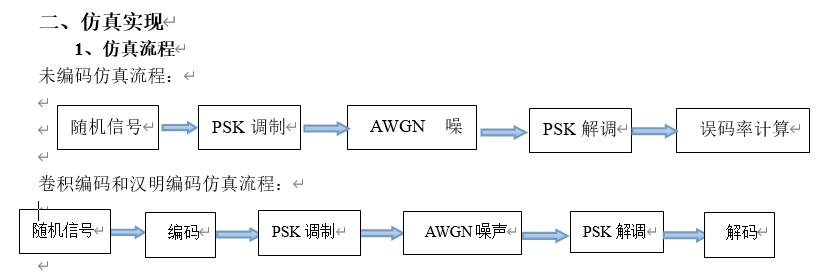
1、未编码、卷积编码和格雷码三种编码，经PSK调制后加AWGN（高斯白噪声），在经过解调和解码得出来的码字误码率都随着信噪比的增加而减小。
2、有仿真图的三条曲线可知，三种编码在PSK调制，外加AWGN后的性能好坏依次是：格雷码 > 卷积编码 > 未编码。

一、编译码的原理
1、卷积码的编译码原理
卷积码：又称连环码，是由伊莱亚斯(P.elias)于1955年提出来的一种非分组码。积码将k个信息比特编成n个比特，但k和n通常很小，特别适合以串行形式进行传输，时延小。卷积码是在一个滑动的数据比特序列上进行模2和操作，从而生成一个比特码流。
卷积码编码：卷积码和分组码的根本区别在于，它不是把信息序列分组后再进行单独编码，而是由连续输入的信息序列得到连续输出的已编码序列。卷积码具有误码纠错的能力，首先被引入卫星和太空的通信中。NASA标准（2，1，6）卷积码生成多项式为：

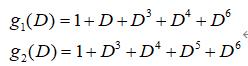
其卷积编码器为：

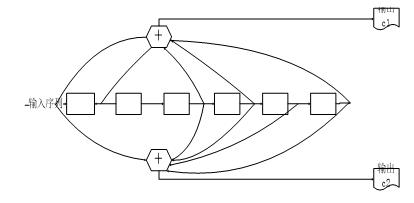
图1.1 K=7，码率为1/2的卷积码编码器
卷积码维特比译码：采用概率译码的基本思想是：把已接收序列与所有可能的发送序列做比较，选择其中码距最小的一个序列作为发送序列。如果接收到L组信息比特，每个符号包括v个比特。接收到的Lv比特序列与2L条路径进行比较，汉明距离最近的那一条路径被选择为最有可能被传输的路劲。当L较大时，使得译码器难以实现。
下面以图2.1的(2，1，3)卷积码编码器所编出的码为例，来说明维特比解码的方法和运作过程。为了能说明解码过程，这里给出该码的状态图，如图2.2所

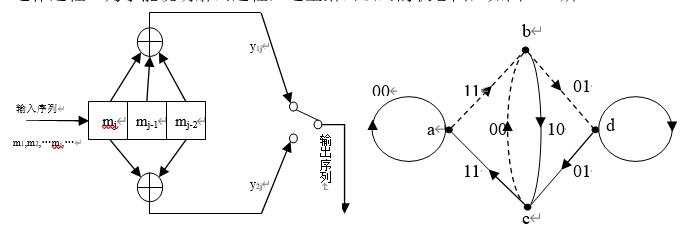
示。维特比译码需要利用图来说明移码过程。根据卷积码画网格的方法，我们可以画出该码的网格图，如图2.3所示。该图设接收到的序列长度为8，所以画8个时间单位，图中分别标以0至7。这里设编码器从a状态开始运作。该网格图的每一条路径都对应着不同的输入信息序列。由于所有可能输入信息序列共有2kL个，因而网格图中所有可能的路径也为2L条。这里节点a=00，b=10，c=01，d=11。

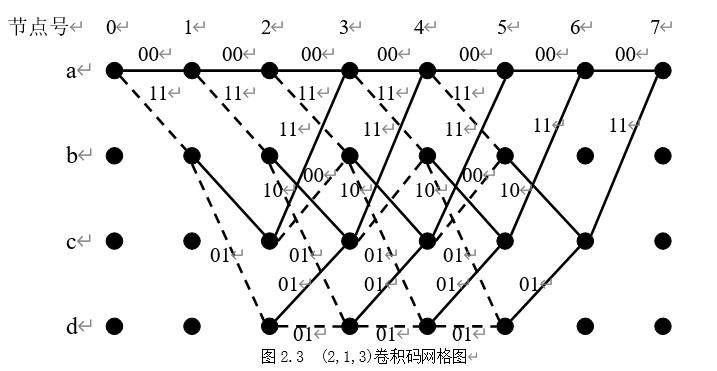
设输入编码器的信息序列为(11011000)，则由编码器对应输出的序列为Y=(1101010001011100)。若收到的序列R=(0101011001011100),对照网格图来说明维特比译码的方法。
首先选择接收序列的前6位序列R1=(010101)同到达第3时刻的可能的8个码序列(即8条路径)进行比较，并计算出码距。该例中到达第3时刻a点的路径序列是(000000)和(111011)，他们与R1的距离分别为3和4；到达第3时刻b点的路径序列是(000011)和(111000)，他们与R1的距离分别为3和4；到达第3时刻c点的路径序列是(001110)和(110101)，他们与R1的距离分别为4和1；到达第3时刻d点的路径序列是(001101)和(110110)，他们与R1的距离分别为2和3。上述每个节点都保留码距较小的路径作为幸存路径，所以幸存路径码序列是(000000)、(000011)、(1101001)和(001101)，如图2.4所示。用于上面类似的方法可以得到第4、5、6、7、8时刻的幸存路径。

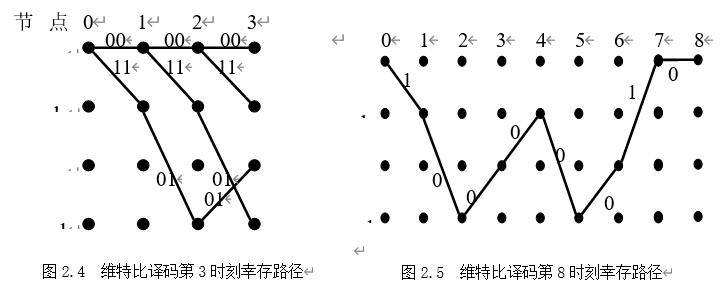
如果2.5所示。由此可看到译码器输出是R’=(1101010001011100)，即可变换成序列(11011000)，恢复了发端原始信息。比较R’和R序列，可以看到在译码过程中已纠正了在码序列第1和第7位上的差错。当然如果差错出现太频繁，以致超出卷积码的纠错能力，还是会发生纠误的。
2、格雷码的编译码原理
格雷码：又称循环码，是线性分组码的一种，所以它具有线性分组码的一般特性，此外还具有循环性。循环码的编码和解码设备都不太复杂，且检(纠)错能力强。它不但可以检测随机的错误，还可以检错突发的错误。（n,k）循环码可以检测长为n-k或更短的任何突发错误，包括首尾相接突发错误。
格雷码的编码原理：有信息码构成信息多项式 ，其中最高幂次为k-1；用 乘以信息多项式m(x)，得到的 ，最高幂次为n-1，该过程相当于把信息码（ ， ，……， ， ）移位到了码字德前k个信息位，其后是r个全为零的监督位；用g(x)除 得到余式r(x),其次数必小于g(x)的次数，即小于（n-k），将此r(x)加于信息位后做监督位，即将r(x)于 相加，得到的多项式必为一码多项式。
格雷码的译码原理：纠错码的译码是该编码能否得到实际应用的关键所在。译码器往往比编码较难实现，对于纠错能力强的纠错码更复杂。根据不同的纠错或检错目的，循环码译码器可分为用于纠错目的和用于检错目的的循环码译码器。当码字c通过噪声信道传送时，会受到干扰而产生错误。如果信道产生的错误图样是e，译码器收到的n重接受矢量是y,则表示为：
上式也可以写成多项式形式：
译码器的任务就是从y(x)中得到 ，然后求的估值码字： 并从中得到信息组 。
循环码译码可按以下三个步骤进行：（1）有接收到的y(x)计算伴随式s(x)；
（2）根据伴随式s(x)找出对应的估值错误图样 ；
（3）计算 ，得到估计码字 。若 ,则译码正确，否则，若 ，则译码错误。

三、主程序

function bianmaa
cycl=50;
snr=0:1:12;
msg=randint(1,100000);
ber0=zeros(1,length(snr));
ber1=zeros(1,length(snr));
trellis=poly2trellis(3,[5 7]);
for n=1:cycl
    for k=1:length(snr)
        modbit0=pskmod(msg,2);
        y0=awgn(modbit0,snr(k),'measured');
        demmsg0=pskdemod(y0,2);
        recode0=reshape(demmsg0',1,[]);
        [num0,rat0]=biterr(recode0,msg);
        ber0(n,k)=rat0;
    end
end
ber0=mean(ber0);
code=convenc(msg,trellis);
modbit1=pskmod(code,2);
for n=1:cycl
    for k=1:length(snr)
        y1=awgn(modbit1,snr(k),'measured');
        demmsg1=pskdemod(y1,2);
        recode1=reshape(demmsg1',1,[]);
        tblen=5;
        decoded1=vitdec(recode1,trellis,tblen,'cont','hard');
  [num1,rat1]=biterr(double(decoded1(tblen+1:end)),msg(1:end-tblen)); 
        ber1(n,k)=rat1;
        ber1(k)=rat1;
    end
end
ber1=mean(ber1);
msg1=randint(70000,1,2);
code=encode1(msg,24,12,); 
modbit2=pskmod(code,2);
for k=1:length(snr)
    y2=awgn(modbit2,snr(k),'measured');
    demmsg2=pskdemod(y2,2);
    recode=reshape(demmsg2',1,[]);
    decodebit=decode1(recode,24,12);
    error2=(decodebit~=msg1');
    errorbits=sum(error2);
    ber2(k)=errorbits/length(msg1);
end
semilogy(snr,ber0,'b-o',snr,ber1,'r-s',snr,0.8*ber2,'k-*');
xlabel('snr/dB');
ylabel('ber');
legend('未编码','卷积编码','格雷码');
title('未编码、卷积编码和格雷码性能比较');
grid on