831. KMP字符串 详解

Posted 2021-05-20 幽殇默

https://www.acwing.com/problem/content/833/

KMP算法是用来解决这种字符串匹配的一个十分经典的算法

首先 用一个朴素的算法来解决本问题

#include<cstring>
#include<string>
#include<iostream>
#include<cstdio>
using namespace std;
int main(void)
{
	int n,m; 
	string s1,s2;
	cin>>n>>s1>>m>>s2;
	int ans=0;
	for(int i=0;i<m;i++)
	{
		bool flag=false;
		int k=i;
		for(int j=0;j<n;j++)
		{
			if(s1[j]!=s2[k++])
			{
				flag=true;
				break;
			}
		}
		if(!flag) cout<<i<<" ";
	}
	return 0;
}

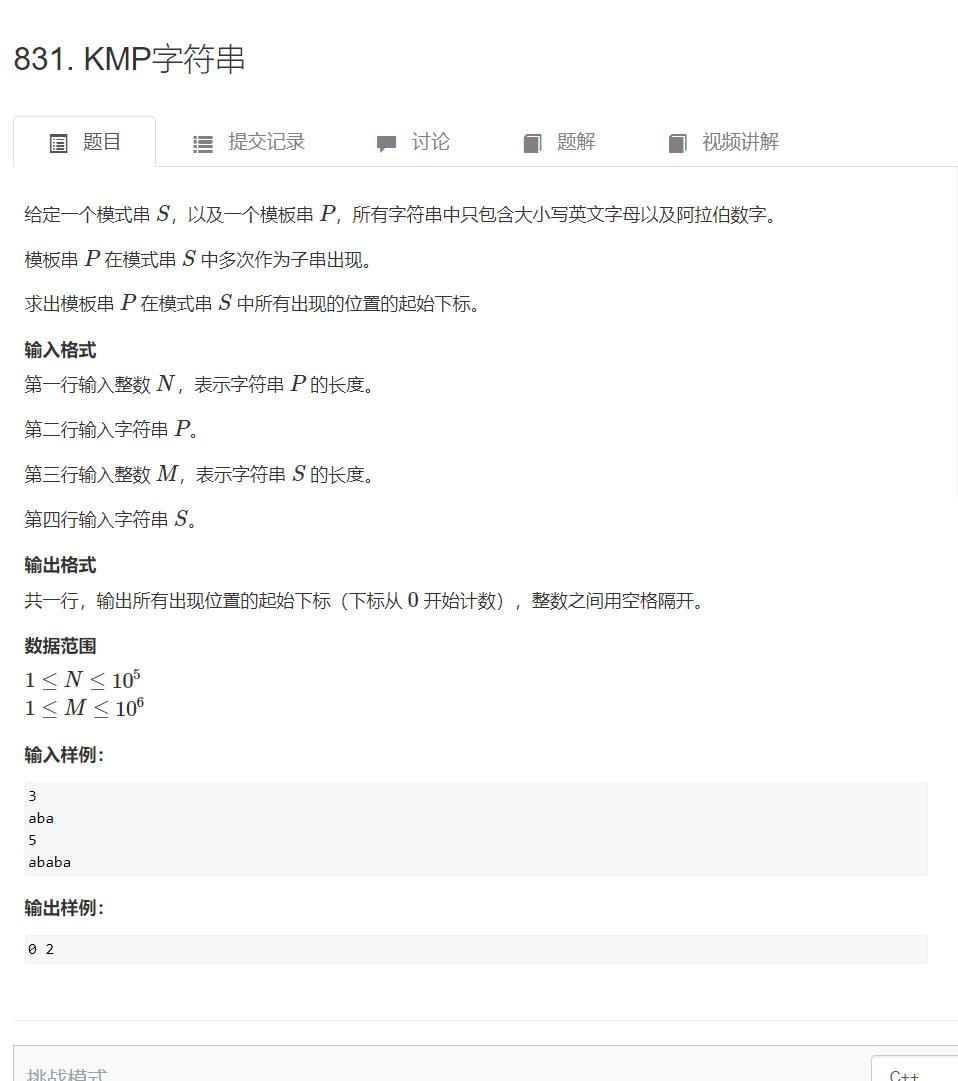
朴素做法的流程如下所示：


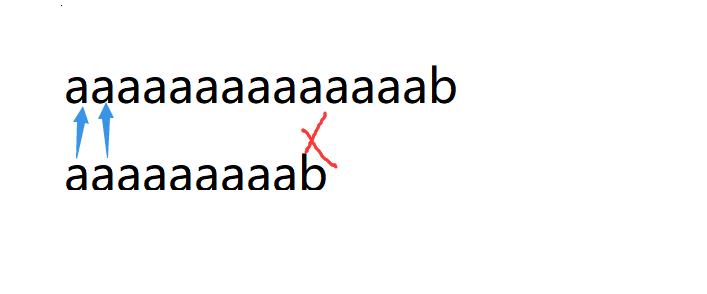
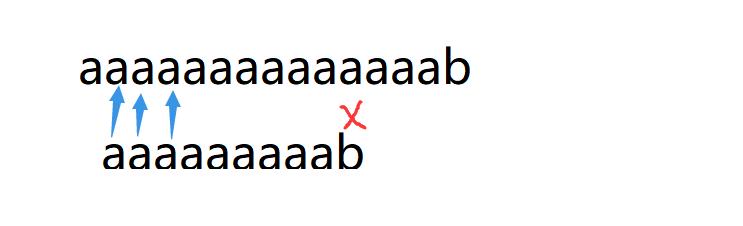
每次向后移动一位，最坏的时间复杂度是 O(nm) 这种做法一定会超时的。
由上图你会发现一个问题就是前面的那一块其实比对了好几次，
那么我们有没有一种方法可以直接不用比较上一次比对的那一部分呢？ 直接比较没有比较过的。
这样就大大的减少了时间复杂度避免了浪费。这就是KMP算法
KMP算法
大致分为如下几步：

• 求其模式串的next[n]数组
• 用模式串和长文串匹配。

next[n] 数组是啥意思？ next[i]的定义是非平凡的最大后缀等于最大前缀
个人见解这个next表，就是找到每次不匹配的时候，之前的字符串的最长前缀和最长后缀，然后移动让最长前缀对到最长后缀的位置，这样就能从不匹配的位置判断，省去了前缀的判断。

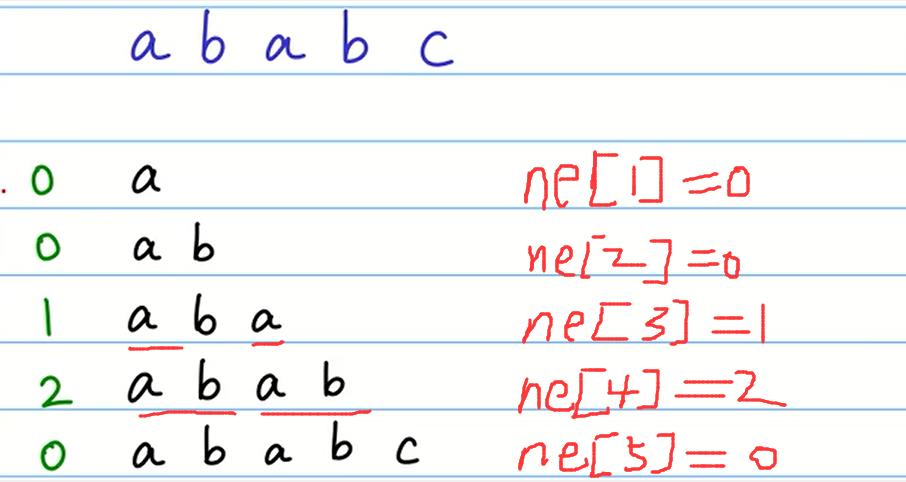
next[i]必须要小于i。

例:   a b a  next[3] 一定小于3   

你不能说最长前缀是 abc 最长后缀是 abc 都是它自己，然后得出 next[ 3 ] =3 。
这显然是错误的，没有意义的。

其实你通过上图你会发现next数组之间的数是有点联系的。

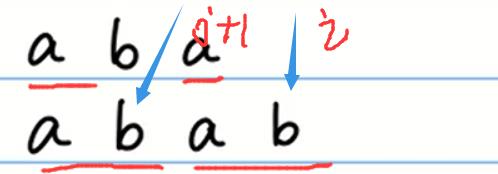
求 next [ 4 ] 的时候，你只要判断新加的字符和之间匹配到的后一个字符相不相等：

• 如果相等 故 next [ 4 ] =next [ 3 ] + 1 = j+1
• 如果不相等 则让 j 回去到 ne[ j ] 直到 j到最开始的零或直到相等。

故模板如下：

for(int i=2,j=0;i<=n;i++)  
// i从2开始   是因为我们的字符串的起始位置是1 而ne[1] =0 不用管故从2开始即可
	{
		while(j&&p[i]!=p[j+1]) j=ne[j];//新加的字符和之前匹配到的后一个字符不相等  就一直回溯到最开始的位置或相等的位置
		if(p[i]==p[j+1]) j++; 
		ne[i]=j;
	} 

匹配
匹配的流程你会发现和求next数组的流程近乎一致。
但是需要注意的是匹配的结果不一定就一个，所以当匹配成功的时候我们的 j 要回到其最大相等的前缀和后缀那里。
故 ： j=ne[ j ] 。

for(int i=1,j=0;i<=m;i++)
	{
		while(j&&s[i]!=p[j+1]) j=ne[j];
		if(s[i]==p[j+1]) j++;
		if(j==n)
		{
			printf("%d,i-n");
			j=ne[j];
		}
	}

完整代码如下：

#include<cstdio>
#include<iostream>
using namespace std;
const int N=1e5+10,M=1e6+10;
char p[N],s[M];
int ne[N];
int n,m;
int main(void)
{
	cin>>n>>p+1>>m>>s+1;
	
	for(int i=2,j=0;i<=n;i++) 
	{
		while(j&&p[i]!=p[j+1]) j=ne[j];
		if(p[i]==p[j+1]) j++;
		ne[i]=j;
	}
	
	for(int i=1,j=0;i<=m;i++)
	{
		while(j&&s[i]!=p[j+1]) j=ne[j];
		if(s[i]==p[j+1]) j++;
		if(j==n)
		{
			j=ne[j];
			cout<<i-n<<" ";
		}
	}
	return 0;
} 

如果各位还不太懂推荐各位看如下几个视频：
https://www.bilibili.com/video/BV1Px411z7Yo
https://www.bilibili.com/video/BV1hW411a7ys