282. 石子合并

Posted 2021-05-20 幽殇默

https://www.acwing.com/problem/content/284/

这是一道典型的区间DP问题，但是却卡了我好久。

这里的集合划分非常的关键: 按最后一次合并时分界线的位置分类。

区间DP的步骤大致如下:

• 枚举区间的距离
• 枚举其左区间端点，距离有了左端点有了右端点自然确定了
• 枚举分界线

代码如下:

#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
const int N=310;
int n;
int s[N];
int f[N][N];
int main(void)
{
	cin>>n;
	for(int i=1;i<=n;i++) cin>>s[i],s[i]+=s[i-1];
	
	for(int len=2;len<=n;len++)//枚举区间距离 , 也可以理解为当前的堆数
	{
		for(int i=1;i<=n-len+1;i++)  //枚举左端点
		{
			int l=i,r=i+len-1;
			f[l][r]=1e8;
			for(int k=l;k<r;k++)  //枚举分界线的位置
			{
				f[l][r]=min(f[l][r],f[l][k]+f[k+1][r]+s[r]-s[l-1]);
			}
		}
		
	}
	
	cout<<f[1][n]<<endl;
	return 0;
}

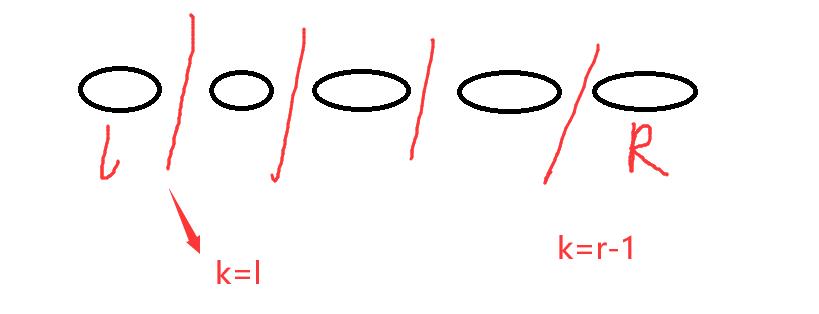
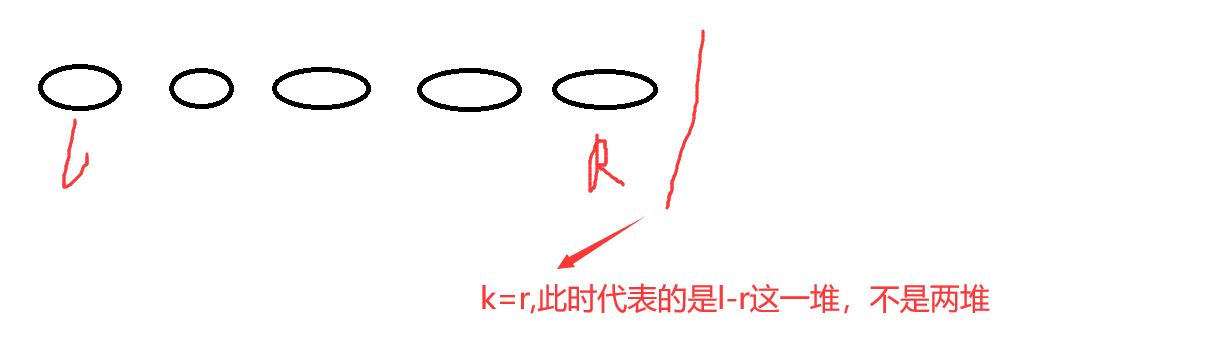
为何不能直接枚举左端点是这样的。
我们每次使用的东西是由上一次更新过的，如果直接枚举左端点使用的可能是没有跟新过的。
比如我们枚举两个点时，求其最小的花费，然后枚举三个点再计算最小的花费，三个点的状态是在二个点的状态基础之上的。
这里可以用分治的思想来理解。