4. 多重背包问题 I

Posted 2021-05-20 幽殇默

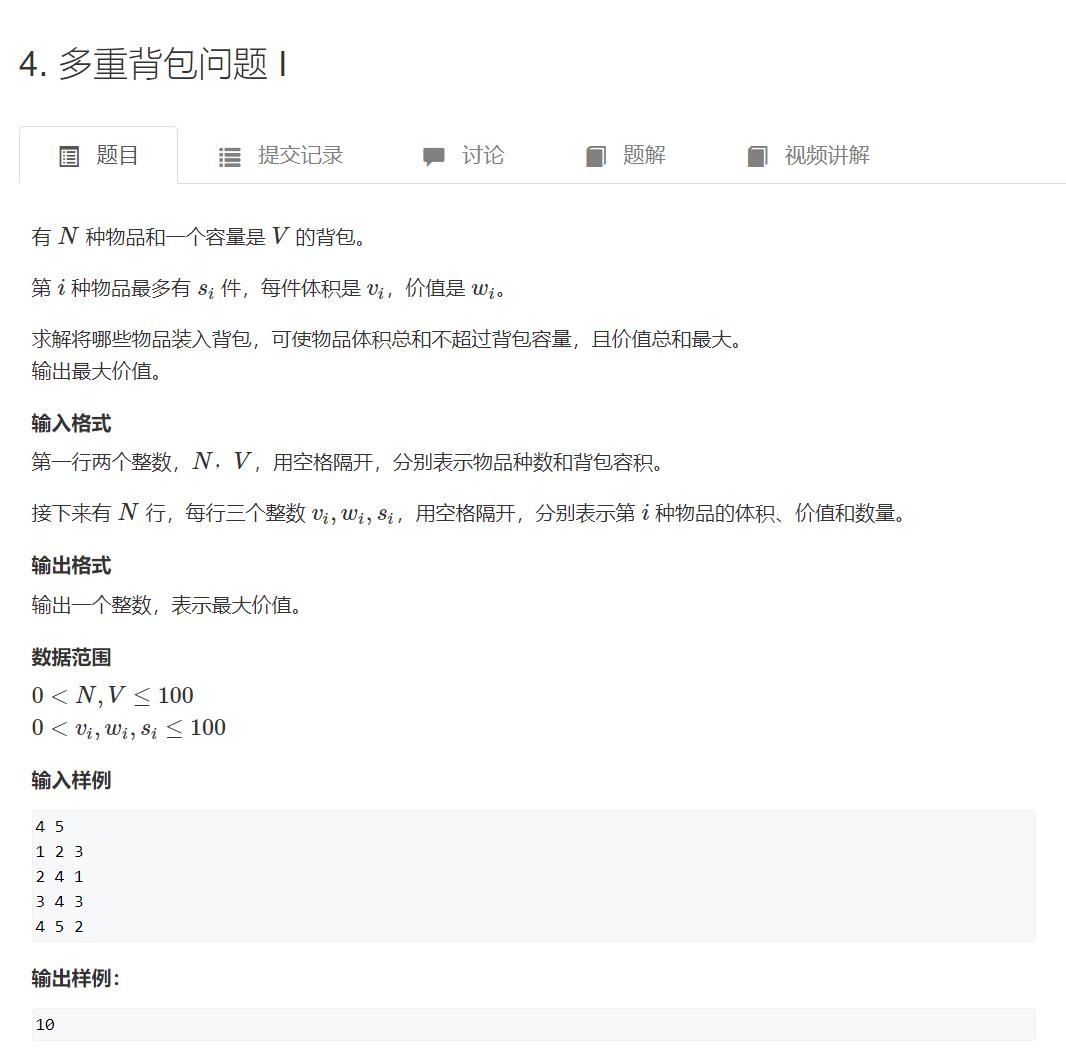
https://www.acwing.com/problem/content/4/

朴素做法:
状态转移方程：f[i][j]=max(f[i][j],f[i-1][j-v[i]*k]+k*w[i]);

#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
const int N=1e3+10;
int f[N][N],v[N],w[N],s[N],n,m;
int main(void)
{
	cin>>n>>m;
	for(int i=1;i<=n;i++) cin>>v[i]>>w[i]>>s[i];
	
	for(int i=1;i<=n;i++)
	{
		for(int j=0;j<=m;j++)
		{
			for(int k=0;k<=s[i]&&k*v[i]<=j;k++)
			{
				f[i][j]=max(f[i][j],f[i-1][j-v[i]*k]+k*w[i]);
			}
		}
	}
	cout<<f[n][m]<<endl;
	return 0;
}

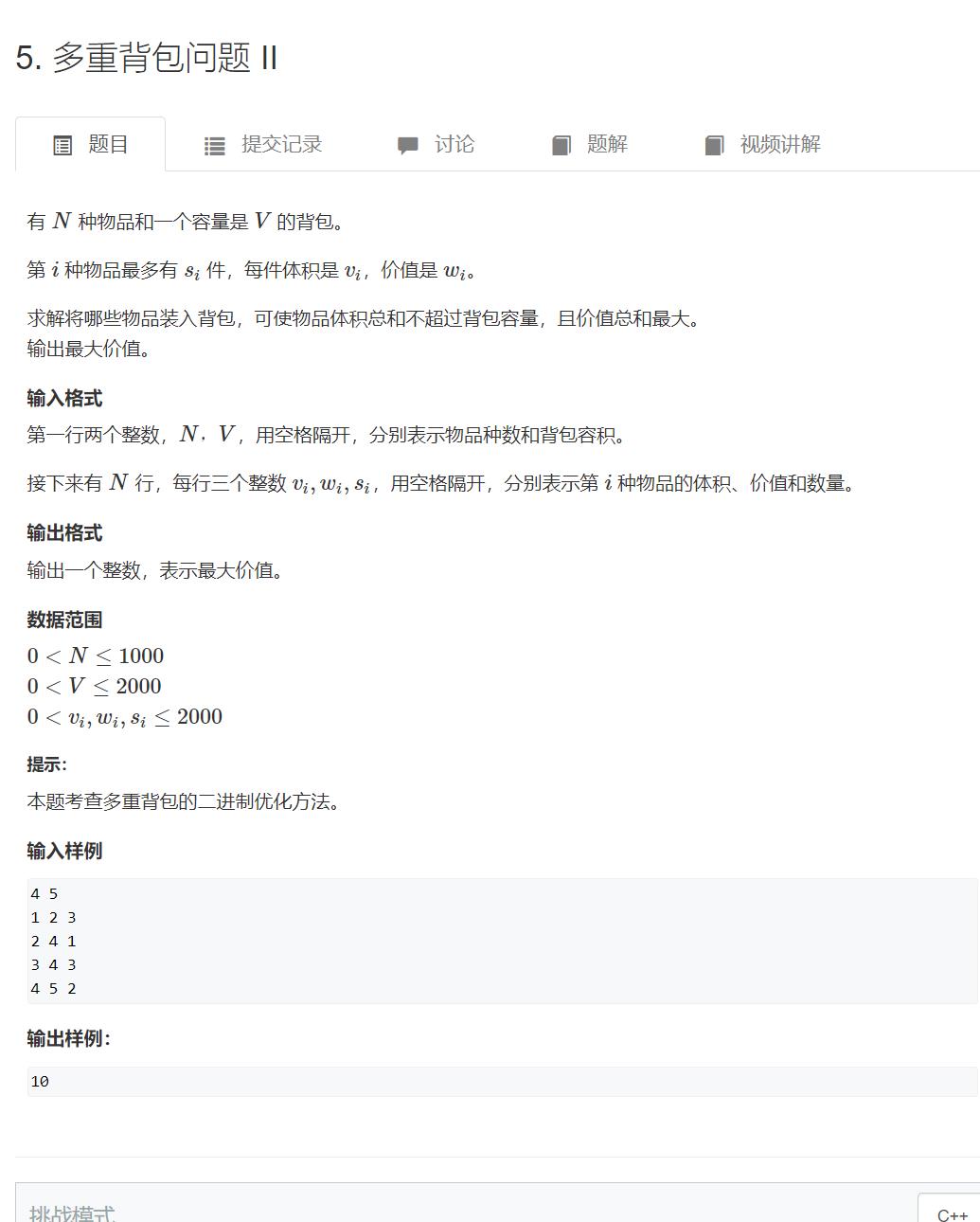
https://www.acwing.com/problem/content/5/

多重背包的本质其实就是一个01背包
二进制优化:

假设: A物品有7个,B物品有3个。 
a1,a2,a3,a4,a5,a6,a7,b1,b2,b3.  
对于每一个我们都有 选和不选两种选择，一共10个物品，枚举的次数：2^10。 
a1,(a2,a3),(a4,a5,a6,a7),(b1),(b2,b3);
对于每一个我们都有 选和不选两种选择，一共5个物品枚举的次数：2^5. 

1代表选，0 代表不选 
此时 
1000000,000   等价于 100,00 
0110000,000   等价于 010,00
....... 
我们每一种的情况都可以用二进制优化的方式组合出来。

#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
const int N=1e5*2+5000;
int f[N],v[N],w[N],cnt,n,m;
int main(void)
{
	cin>>n>>m;
	for(int i=1;i<=n;i++)
	{
		int a,b,s;
		cin>>a>>b>>s;
		int k=1;
		while(k<=s)
		{
			cnt++;
			v[cnt]=a*k;
			w[cnt]=b*k;
			s-=k;
			k=k*2;
		}
		if(s>0)
		{
			cnt++;
			v[cnt]=a*s;
			w[cnt]=b*s; 
		}
	}
	
	n=cnt;
	for(int i=1;i<=n;i++)
	{
		for(int j=m;j>=v[i];j--)
		f[j]=max(f[j],f[j-v[i]]+w[i]);
	}
	cout<<f[m]<<endl;
	return 0;
}