大话数据结构C语言46 最小生成树（克鲁斯卡尔算法）

Posted 2021-05-20 是CodeAllen

欢迎关注我的公众号是【CodeAllen】，关注回复【1024】获取资源
程序员技术交流①群：736386324 ，程序员技术交流②群：371394777    

无论是普里姆算法（Prim）还是克鲁斯卡尔算法（Kruskal），他们考虑问题的出发点都是：为使生成树上边的权值之和达到最小，则应使生成树中每一条边的权值尽可能的小。 

 

普里姆算法是以某顶点为起点，逐步找各个顶点上最小权值的边来构建最小生成树的

 

kruskal.c

int Find(int *parent, int f)
{
    while( parent[f] > 0 )
    {
        f = parent[f];
    }
    
    return f;
}

// Kruskal算法生成最小生成树
void MiniSpanTree_Kruskal(MGraph G)
{
    int i, n, m;
    Edge edges[MAGEDGE];    // 定义边集数组
    int parent[MAXVEX];     // 定义parent数组用来判断边与边是否形成环路
    
    for( i=0; i < G.numVertexes; i++ )
    {
        parent[i] = 0;
    }
    
    for( i=0; i < G.numEdges; i++ )
    {
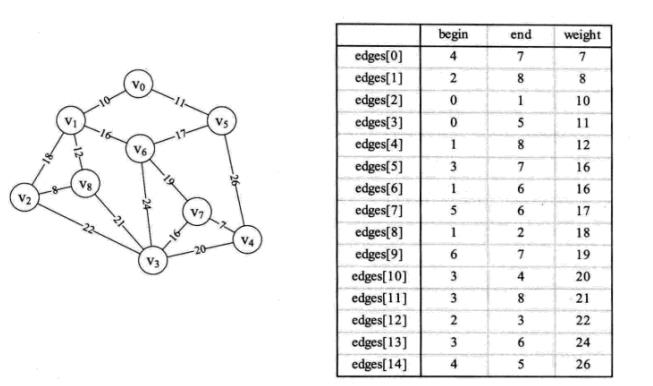
        n = Find(parent, edges[i].begin);   // 4 2 0 1 5 3 8 6 6 6 7
        m = Find(parent, edges[i].end);     // 7 8 1 5 8 7 6 6 6 7 7
        
        if( n != m )        // 如果n==m，则形成环路，不满足！
        {
            parent[n] = m;  // 将此边的结尾顶点放入下标为起点的parent数组中，表示此顶点已经在生成树集合中
            printf("(%d, %d) %d ", edges[i].begin, edges[i].end, edges[i].weight);
        }
    }
}