计算机组成原理——移位运算

Posted 2021-05-19 流楚丶格念

文章目录

• 算数移位
• • 原码的算数移位
  • 反码的算数移位
  • 补码的算数移位
• 逻辑移位
• • 逻辑移位的应用举例
• 循环移位

移位：通过改变各个数码位和小数点的相对位置，从而改变各数码位的位权。可用移位运算实现乘法、除法

算数移位

原码的算数移位

例如原码为 10101000 进行算数移位

原码的算数移位——符号位保持不变，仅对数值位进行移位。

• 右移：高位补0，低位舍弃。若舍弃的位=0，则相当于÷2；若舍弃的位≠0，则会丢失精度
• 左移：低位补0，高位舍弃。若舍弃的位=0，则相当于×2；若舍弃的位≠0，则会出现严重误差

反码的算数移位

反码的算数移位——正数的反码与原码相同，因此对正数反码的移位运算也和原码相同。

• 右移：高位补0，低位舍弃。
• 左移：低位补0，高位舍弃

反码的算数移位——负数的反码数值位与原码相反，因此负数反码的移位运算规则如下，

• 右移：高位补1，低位舍弃。
• 左移：低位补1，高位舍弃。

补码的算数移位

补码的算数移位——正数的补码与原码相同，因此对正数补码的移位运算也和原码相同。

• 右移：高位补0，低位舍弃。
• 左移：低位补0，高位舍弃。

补码的算数移位——负数补码=反码末位+1 导致反码最右边几个连续的1都因进位而变为0，直到进位碰到第一个0为止。

规律——负数补码中，最右边的1及其右边同原码。最右边的1的左边同反码
负数补码的算数移位规则如下：

• 右移（同反码）：高位补1，低位舍弃。
• 左移（同原码）：低位补0，高位舍弃。

逻辑移位

• 逻辑右移：高位补0，低位舍弃。
• 逻辑左移：低位补0，高位舍弃。

可以把逻辑移位看作是对“无符号数”的算数移位

逻辑移位的应用举例

例如颜色RGB分别存储的数据为：
R = 102 01100110
G = 139 10001011
B = 139 10001011

需要将三个灰度值合成一个才能成彩色图像

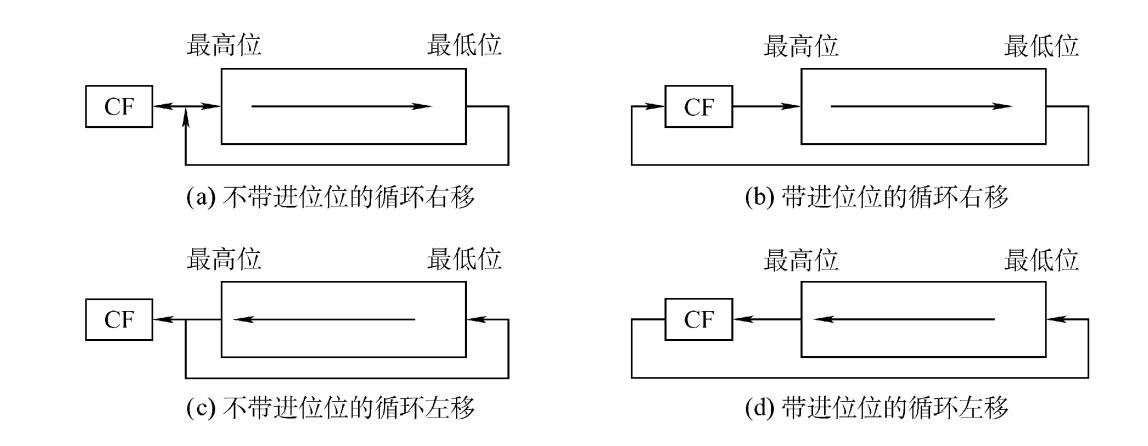
循环移位