红黑树插入删除详细步骤动画演示与AVL树的区别

Posted 2021-05-18 PoetryAndTheDistance

目录

红黑树认识

红黑树插入

红黑树删除

红黑树和AVL树（平衡二叉树）的定义、特点以及两者的区别

定义

性质

区别

---

红黑树动画在线演示

红黑树认识

红黑树是一种二叉排序树，先来看一下二叉排序树的基本性质：

若它的左子树不空，则左子树上所有节点的值均小于它的根节点的值； 若它的右子树不空，则右子树上所有节点的值均大于它的根节点的值； 它的左、右子树也分别为二叉排序树
红黑树是每个节点都带有颜色属性的二叉查找树，颜色或红色或黑色。在二叉查找树强制一般要求以外，对于任何有效的红黑树我们增加了如下的额外要求:

1. 节点是红色或黑色。
2. 根节点是黑色。
3. 每个叶节点（NIL节点，空节点）是黑色的。
4. 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
5. 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。

这些约束强制了红黑树的关键性质: 从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。结果是这个树大致上是平衡的。 因为操作比如插入、删除和查找某个值的最坏情况时间都要求与树的高度成比例 ，这个在高度上的理论上限允许 红黑树在最坏情况下都是高效的 ，而不同于普通的二叉查找树。
性质4导致了路径不能有两个毗连的红色节点。所以最短的可能路径都是黑色节点。 最长的可能路径有交替的红色和黑色节点。 因为根据性质5所有最长的路径都有相同数目的黑色节点，这就表明了没有路径能多于任何其他路径的两倍长。
下图，就是一个红黑树的例子：

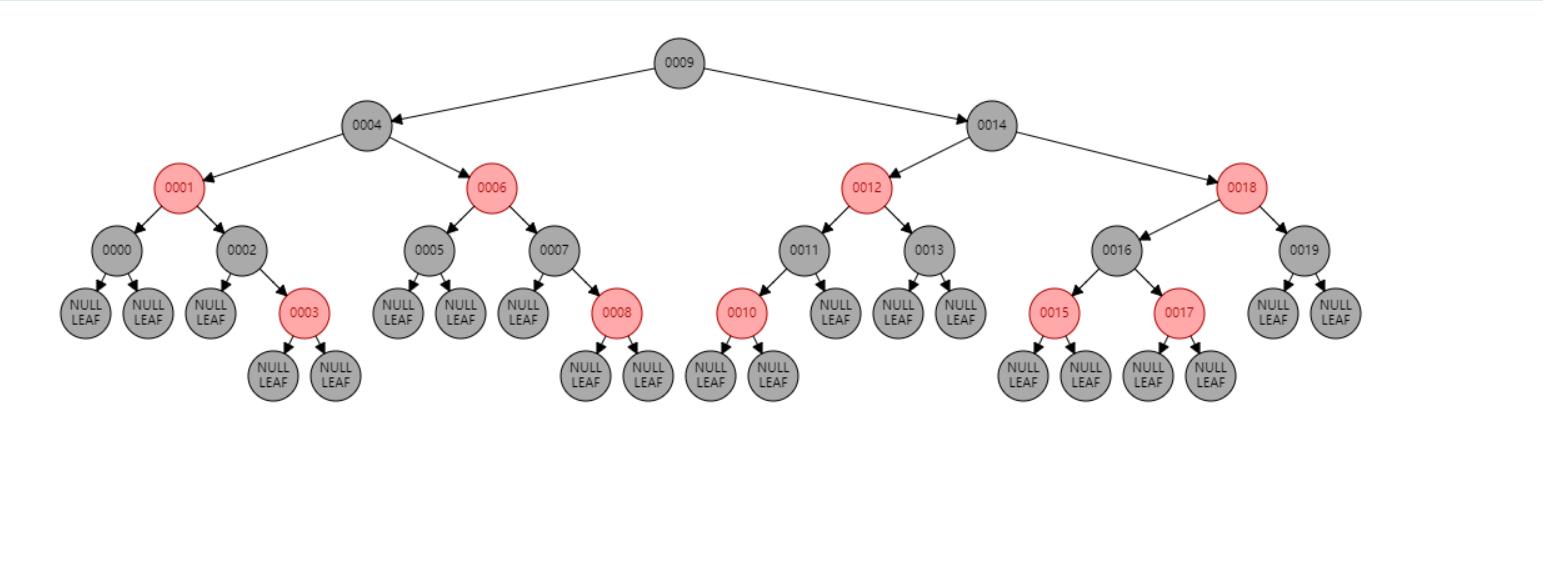
红黑树插入

为了实现一个红黑树的插入操作，我们需要完成2个步骤

1. 先对一个节点进行插入操作
2. 该节点插入后即被染成红色，这可能破坏了红黑树的5个性质，所以，我们要实现插入新节点后的一系列旋转和重染色操作

红黑树插入时所有的情况有以下几种：

1. 情况一：节点N位于树的根上，没有父节点。//符合红黑树性质
2. 情况二：节点N的父节点P是黑色。//符合红黑树性质
3. 情况三：父节点P、叔叔节点U，都为红色。//祖父节点G染红色，父节点P和叔叔节点U染黑色
4. 情况四：节点N和父节点P都是红色，叔叔节点U是黑色或NIL，节点N为左子节点，父节点P又是其父G的左子节点。//右旋 或 父节点P染黑色，兄弟节点B染红色
5. 情况五：节点N和父节点P都是红色，叔叔节点U是黑色或NIL，节点N为右子节点，父节点P又是其父G的左子节点。//左旋 或 父节点P染黑色，兄弟节点B染红色
6. 情况六：节点N和父节点P都是红色，叔叔节点U是黑色或NIL，节点N为左子节点，父节点P又是其父G的右子节点。//右旋 或 父节点P染黑色，兄弟节点B染红色
7. 情况七：节点N和父节点P都是红色，叔叔节点U是黑色或NIL，节点N为右子节点，父节点P又是其父G的右子节点。//左旋 或 父节点P染黑色，兄弟节点B染红色

以及旋转过程中的情况：

1. 情况八：根节点R是红色。//根节点R染黑色
2. 情况九：父节点P、祖父节点G，都为红色。//父节点P染黑色，兄弟节点B染红色

以下的图片是依次插入这些节点：12 1 9 2 0 11 7 19 4 15 18 5 14 13 10 16 6 3 8 17的全程演示图，已经把所有的几种插入情况，都全部涉及到了：

 

插入 12

插入节点

情况一：节点N位于树的根上，没有父节点。//符合红黑树性质

插入 1

插入节点

情况二：节点N的父节点P是黑色。//符合红黑树性质

插入 9

插入节点

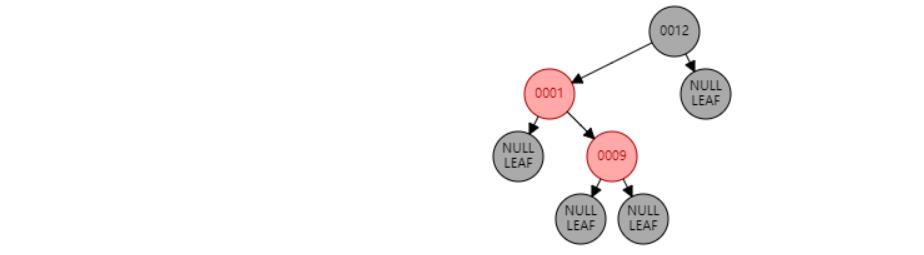
情况五：节点N和父节点P都是红色，叔叔节点U是黑色或NIL，节点N为右子节点，父节点P又是其父G的左子节点。//左旋 或 父节点P染黑色，兄弟节点B染红色

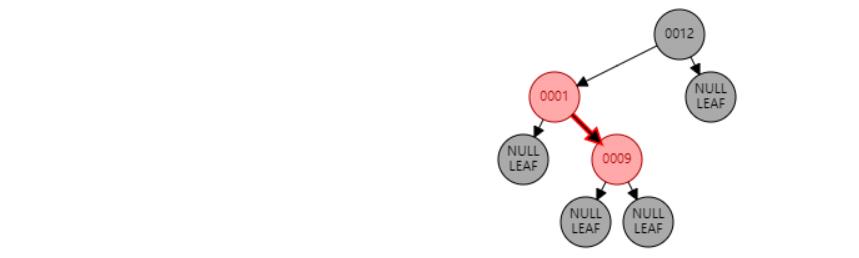
情况四：节点N和父节点P都是红色，叔叔节点U是黑色或NIL，节点N为左子节点，父节点P又是其父G的左子节点。//右旋 或 父节点P染黑色，兄弟节点B染红色

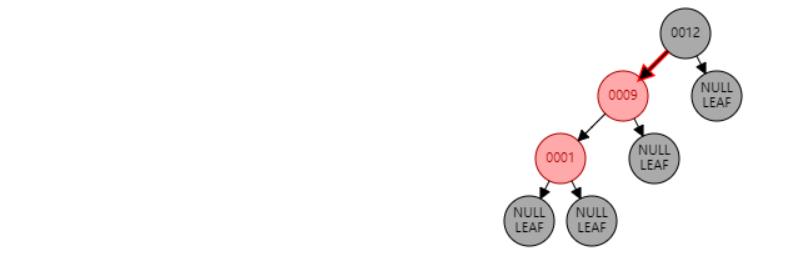
情况八：根节点R是红色。//根节点R染黑色

插入 2

插入节点

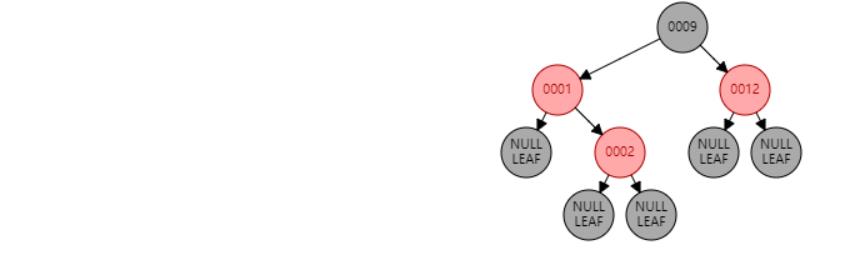
情况三：父节点P、叔叔节点U，都为红色。//祖父节点G染红色，父节点P和叔叔节点U染黑色

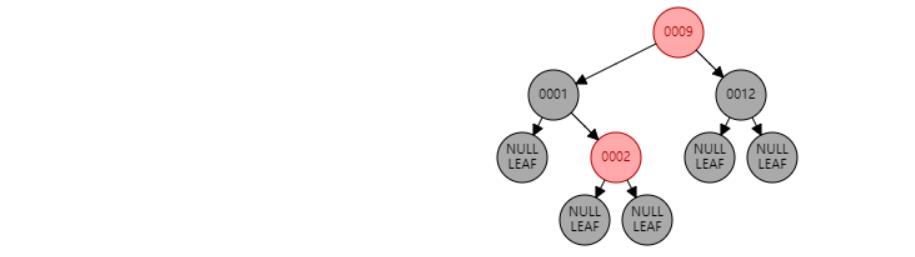
情况八：根节点R是红色。//根节点R染黑色

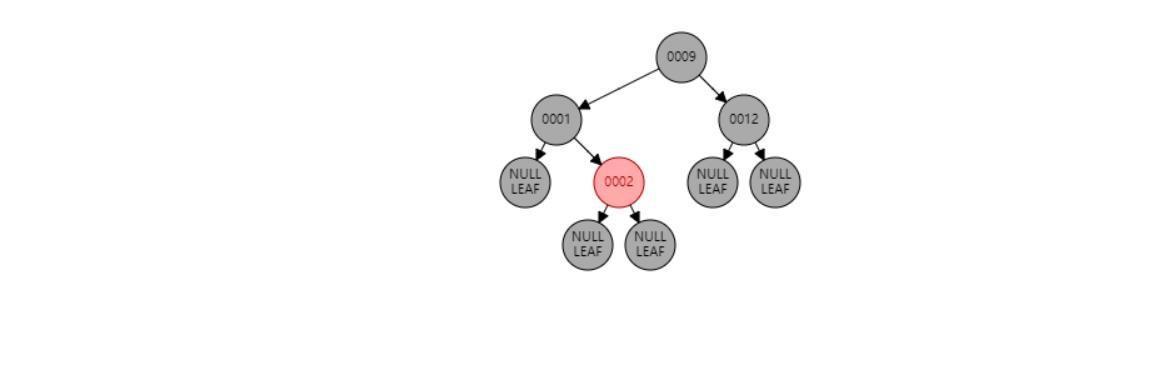
插入 0

插入节点

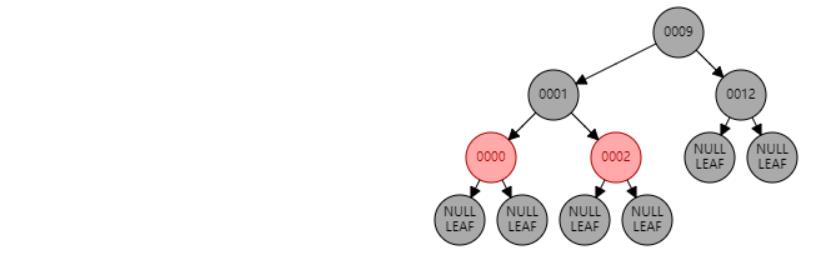
情况二：节点N的父节点P是黑色。//符合红黑树性质

插入 11

插入节点

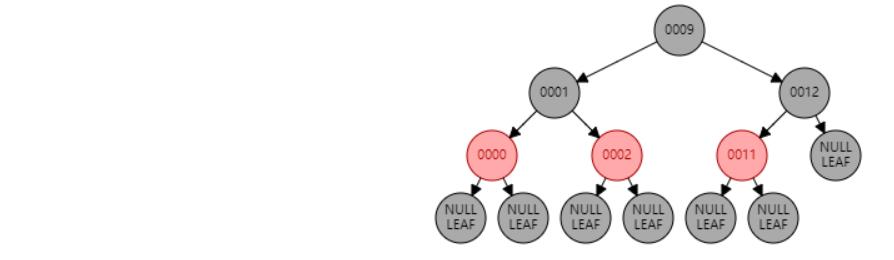
情况二：节点N的父节点P是黑色。//符合红黑树性质

插入 7

插入节点

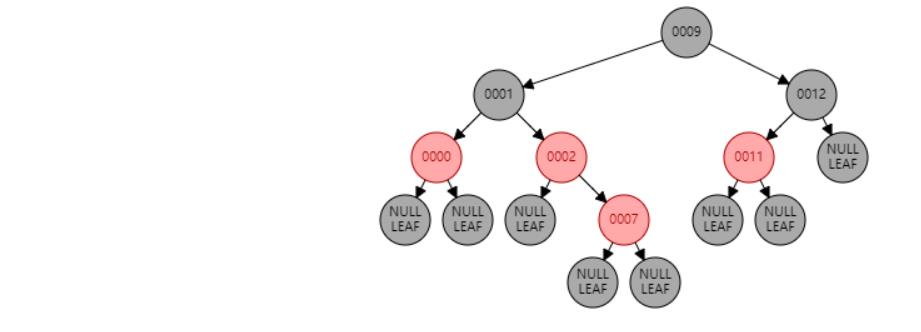
情况三：父节点P、叔叔节点U，都为红色。//祖父节点G染红色，父节点P和叔叔节点U染黑色

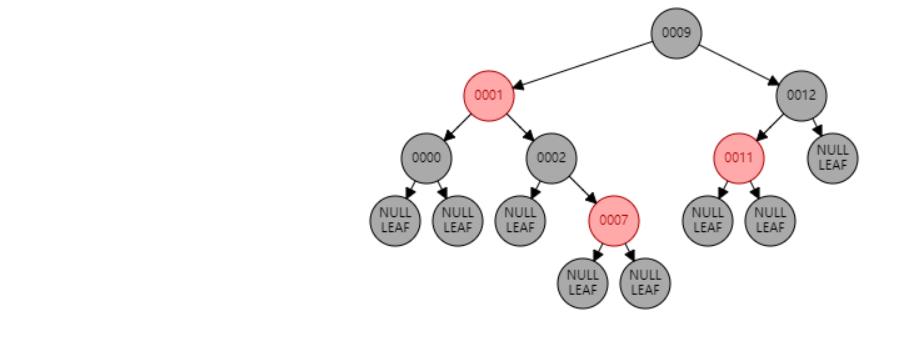
插入 19

插入节点

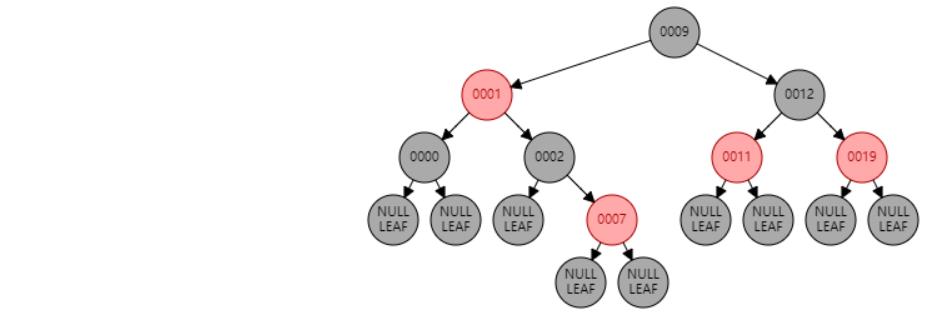
情况二：节点N的父节点P是黑色。//符合红黑树性质

插入 4

插入节点

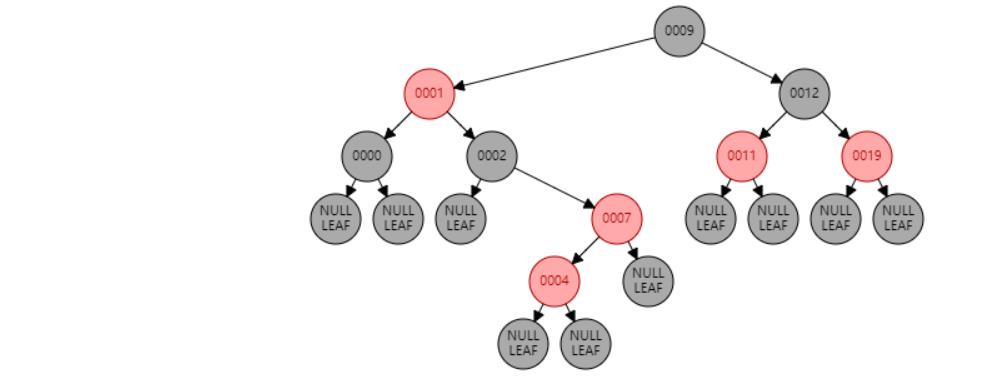
情况六：节点N和父节点P都是红色，叔叔节点U是黑色或NIL，节点N为左子节点，父节点P又是其父G的右子节点。//右旋 或 父节点P染黑色，兄弟节点B染红色

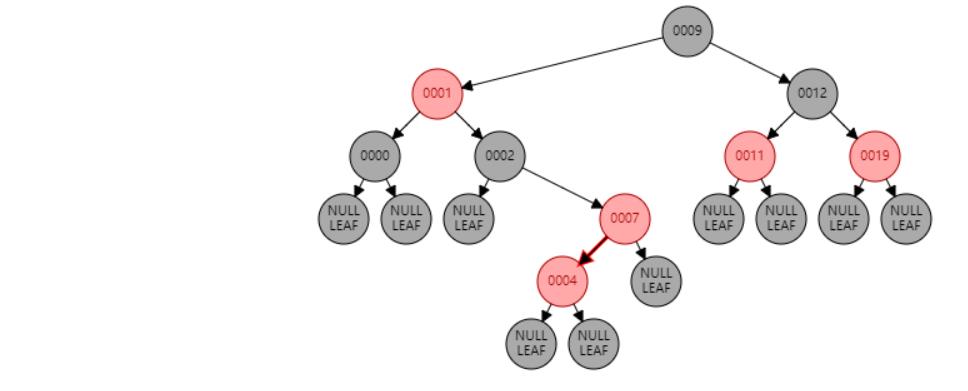
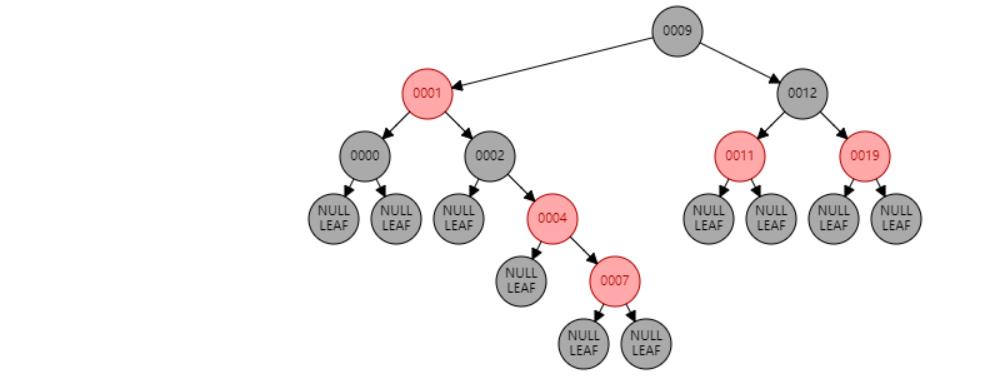
情况七：节点N和父节点P都是红色，叔叔节点U是黑色或NIL，节点N为右子节点，父节点P又是其父G的右子节点。//左旋 或 父节点P染黑色，兄弟节点B染红色

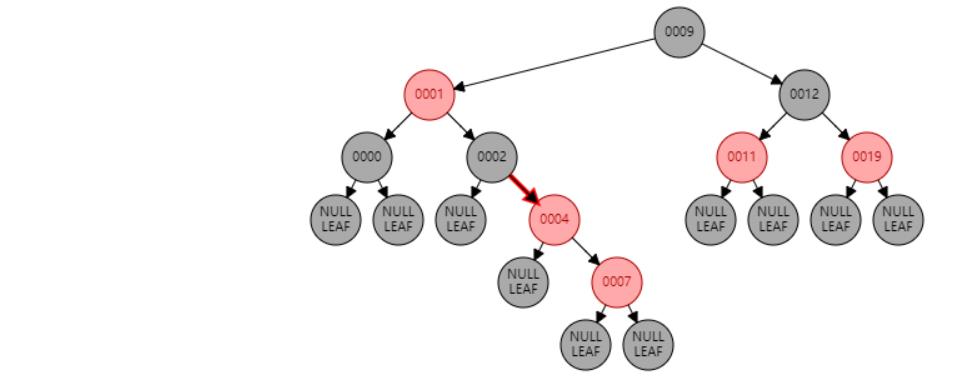
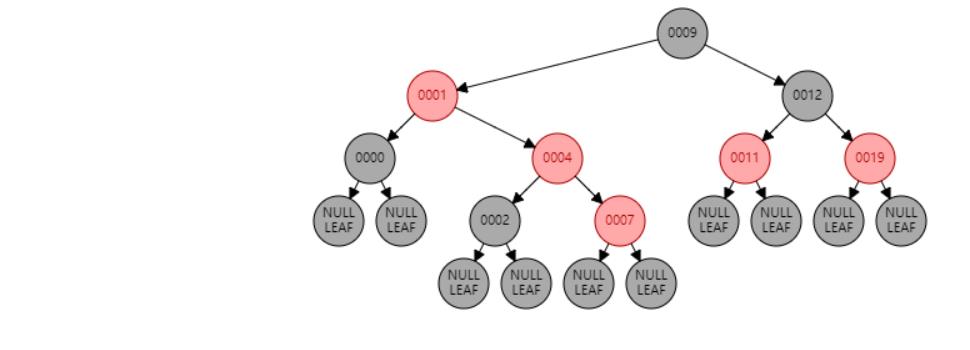
情况九：父节点P、祖父节点G，都为红色。//父节点P染黑色，兄弟节点B染红色

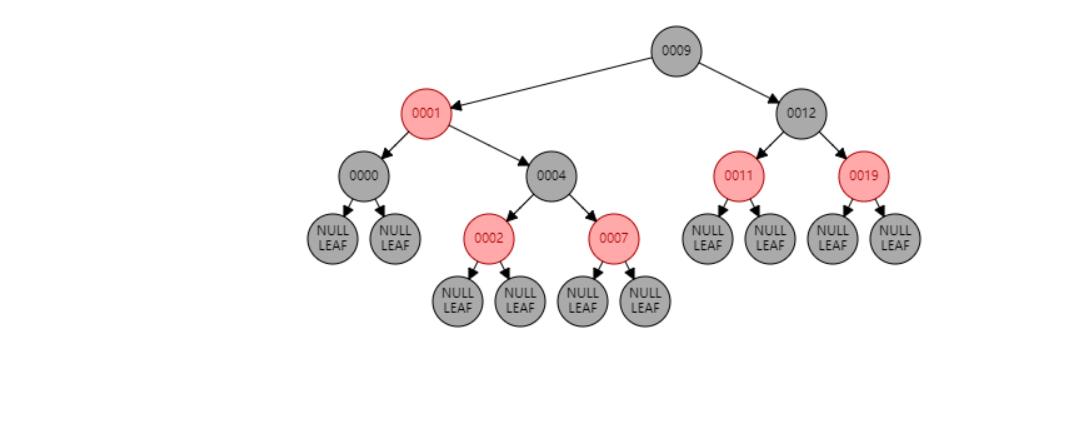
插入 15

插入节点

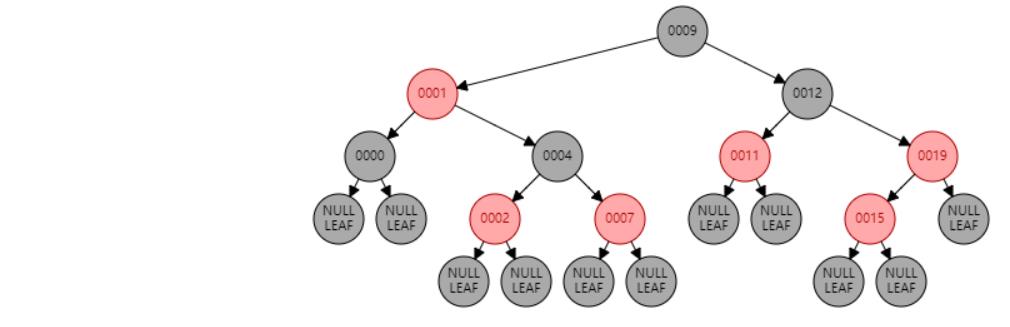
情况三：父节点P、叔叔节点U，都为红色。//祖父节点G染红色，父节点P和叔叔节点U染黑色

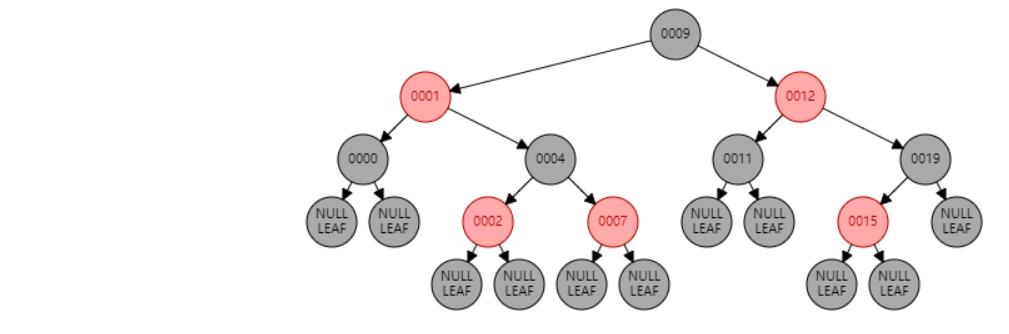
插入 18

插入节点

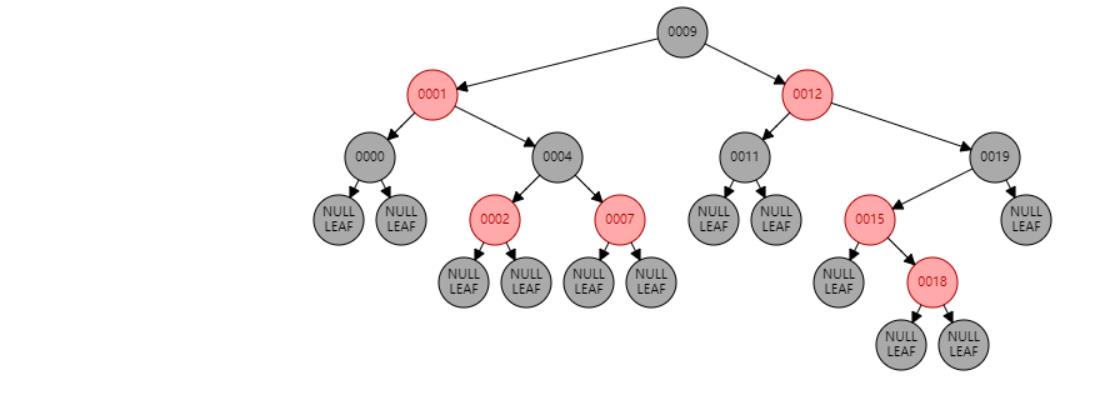
情况五：节点N和父节点P都是红色，叔叔节点U是黑色或NIL，节点N为右子节点，父节点P又是其父G的左子节点。//左旋 或 父节点P染黑色，兄弟节点B染红色

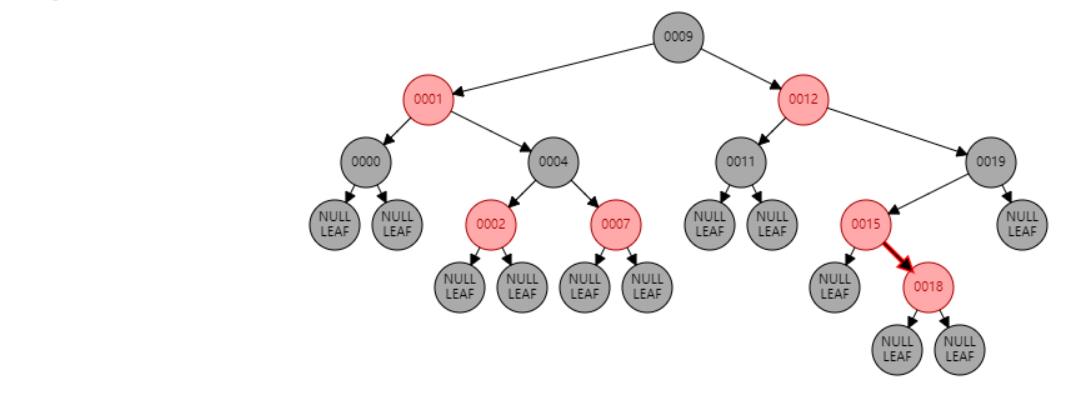
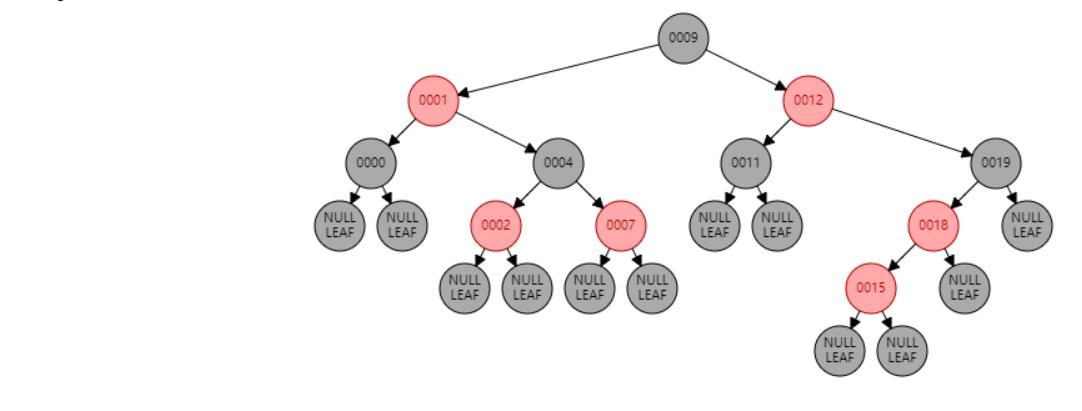
情况四：节点N和父节点P都是红色，叔叔节点U是黑色或NIL，节点N为左子节点，父节点P又是其父G的左子节点。//右旋 或 父节点P染黑色，兄弟节点B染红色

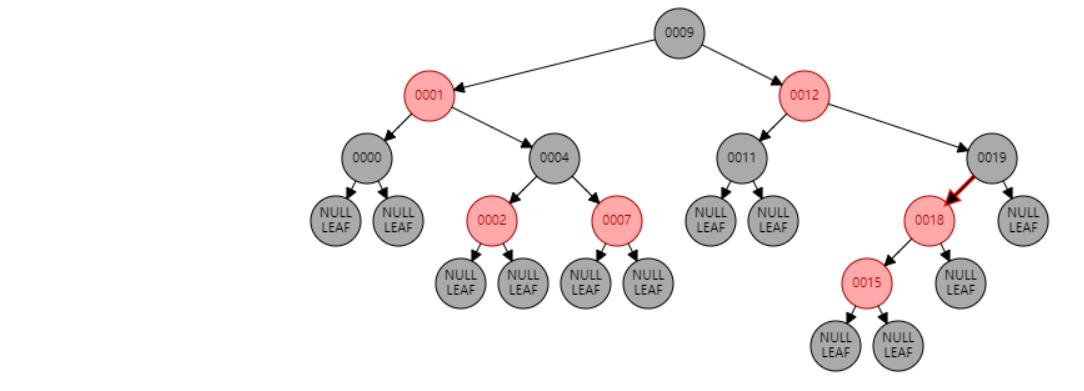
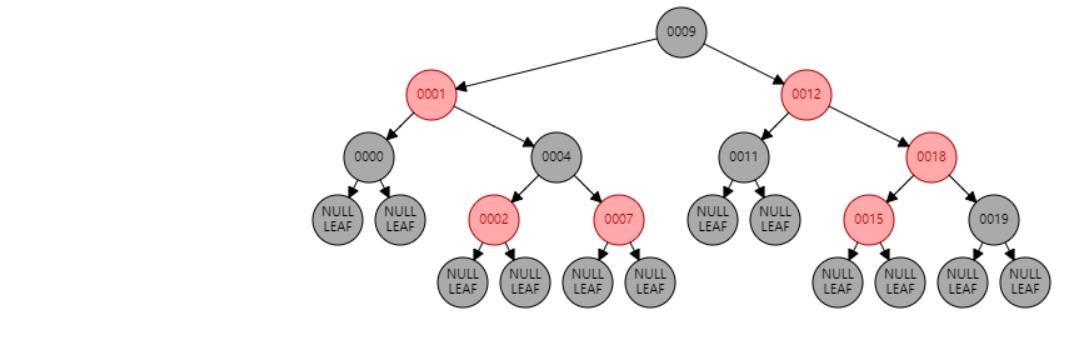
情况九：父节点P、祖父节点G，都为红色。//父节点P染黑色，兄弟节点B染红色

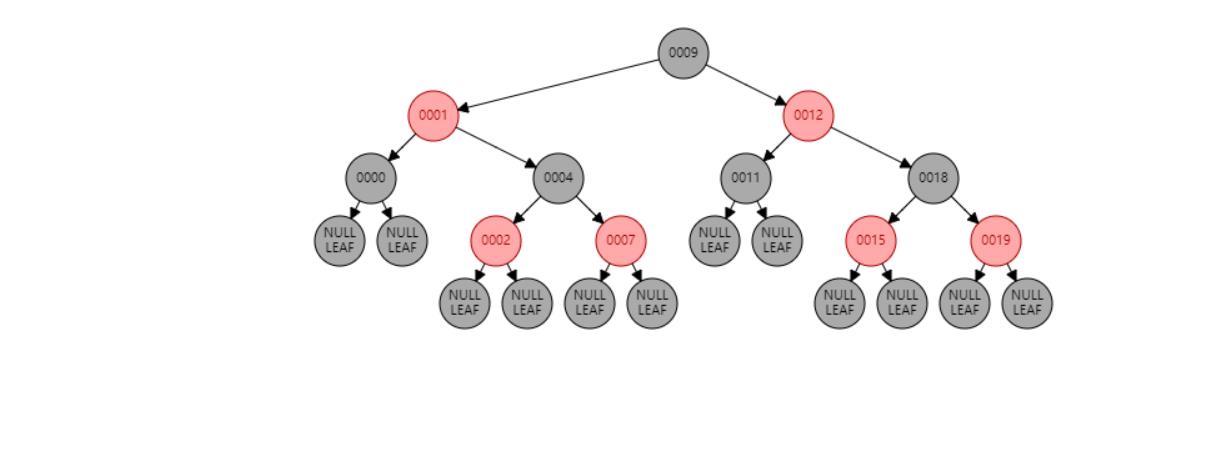
插入 5

插入节点

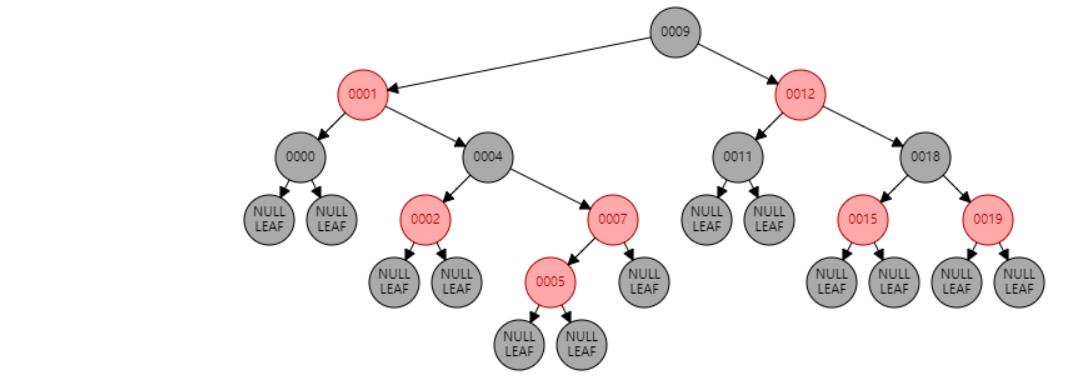
情况三：父节点P、叔叔节点U，都为红色。//祖父节点G染红色，父节点P和叔叔节点U染黑色

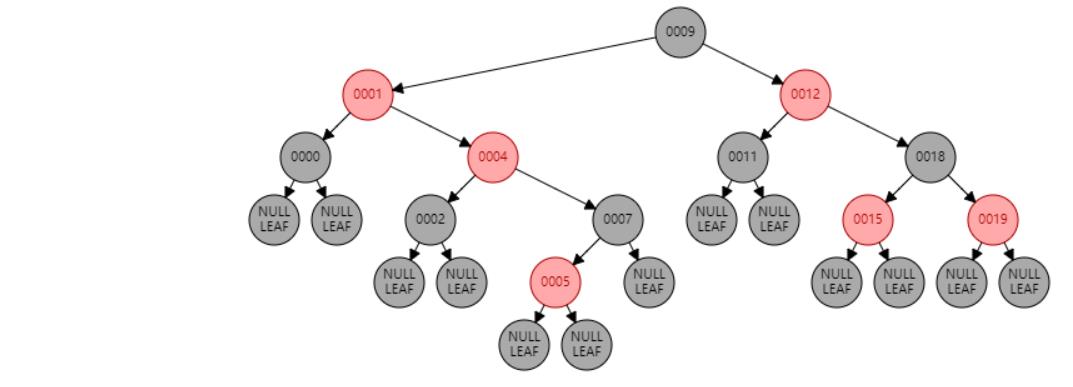
情况三：父节点P、叔叔节点U，都为红色。//祖父节点G染红色，父节点P和叔叔节点U染黑色

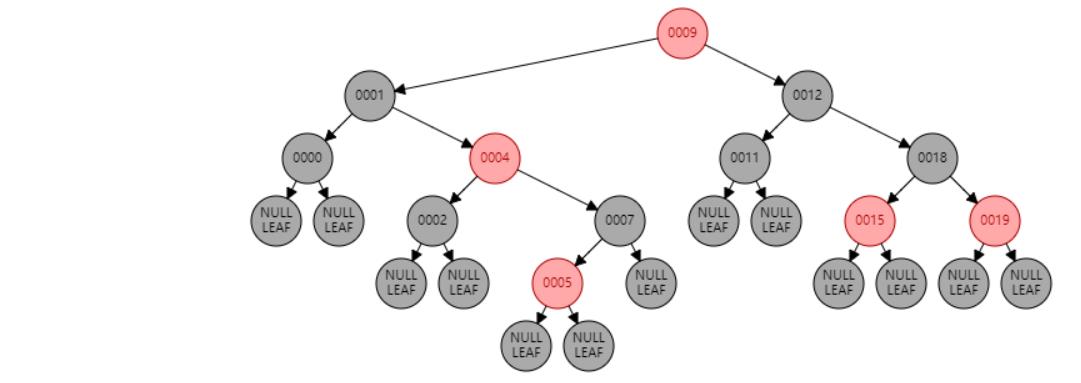
情况八：根节点R是红色。//根节点R染黑色

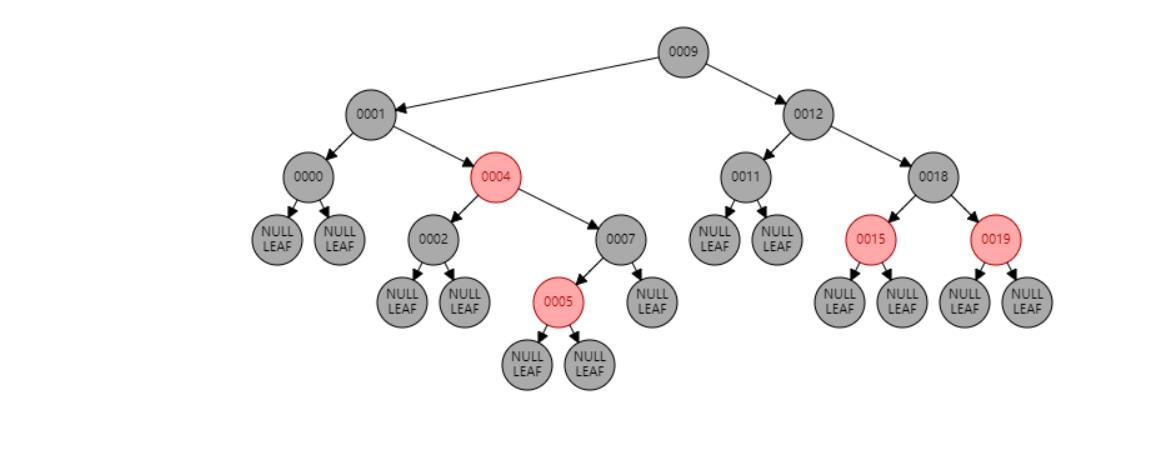
插入 14

插入节点

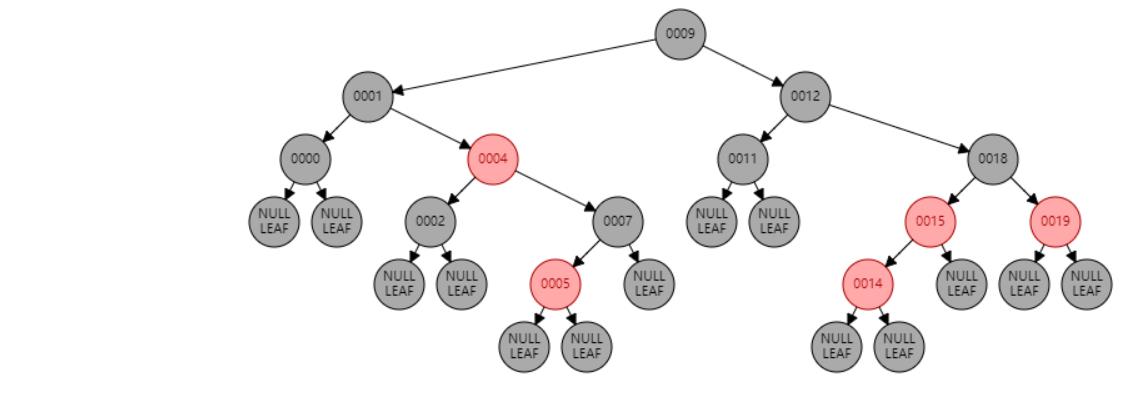
情况三：父节点P、叔叔节点U，都为红色。//祖父节点G染红色，父节点P和叔叔节点U染黑色

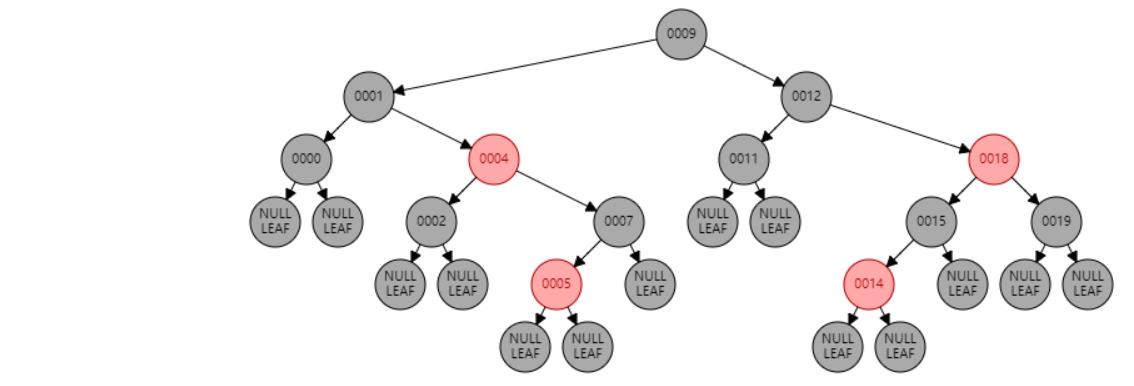
插入 13

插入节点

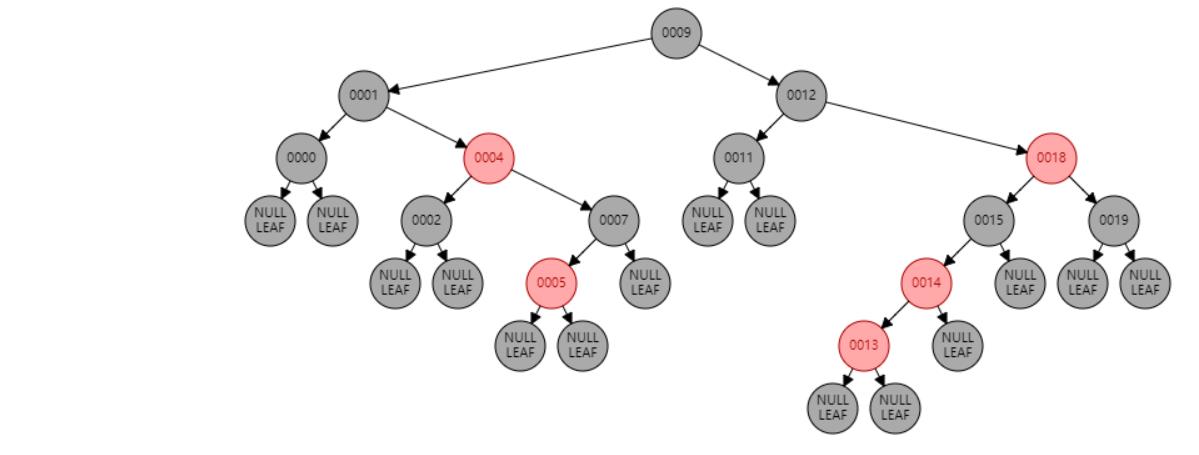
情况四：节点N和父节点P都是红色，叔叔节点U是黑色或NIL，节点N为左子节点，父节点P又是其父G的左子节点。//右旋 或 父节点P染黑色，兄弟节点B染红色

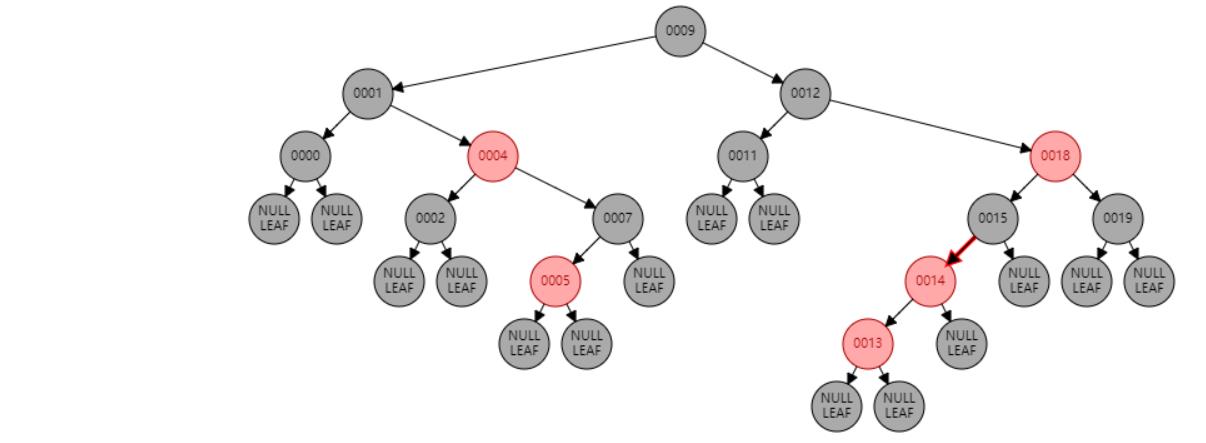
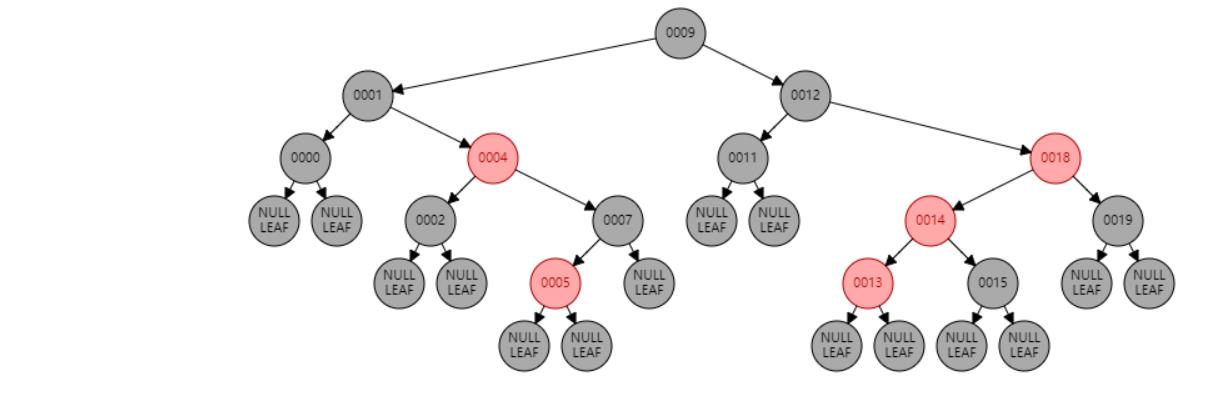
情况九：父节点P、祖父节点G，都为红色。//父节点P染黑色，兄弟节点B染红色

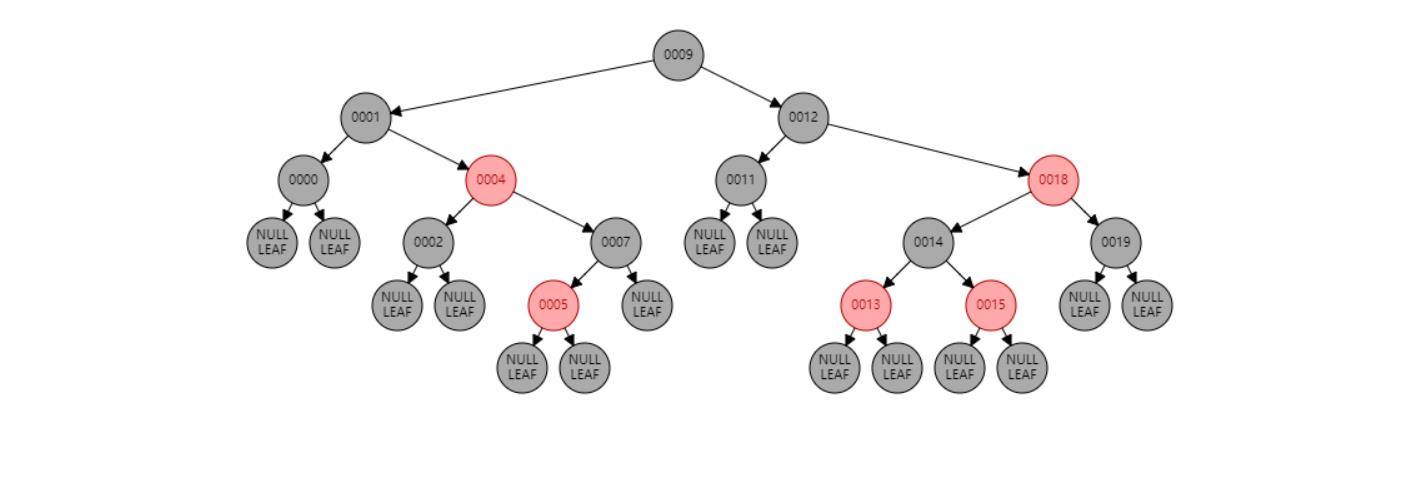
插入 10

插入节点

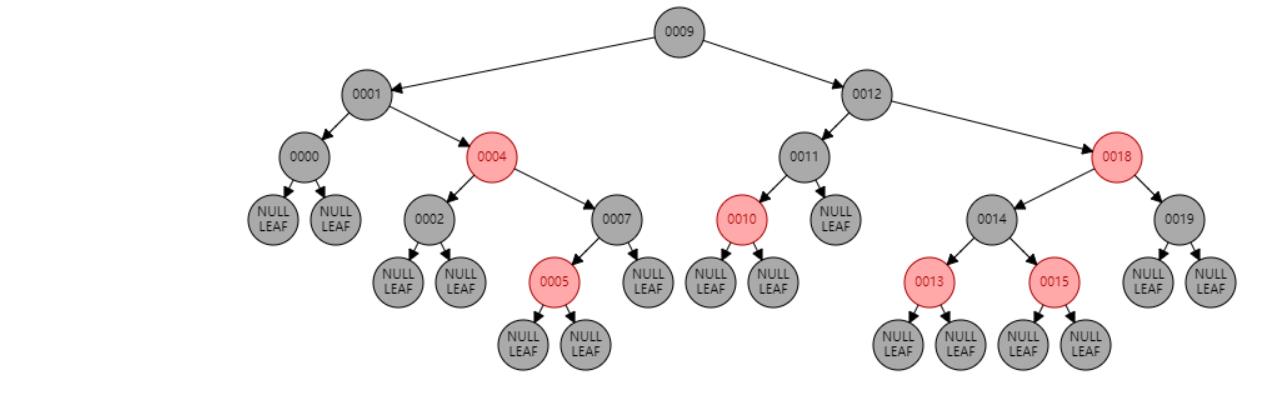
情况二：节点N的父节点P是黑色。//符合红黑树性质

插入 16

插入节点

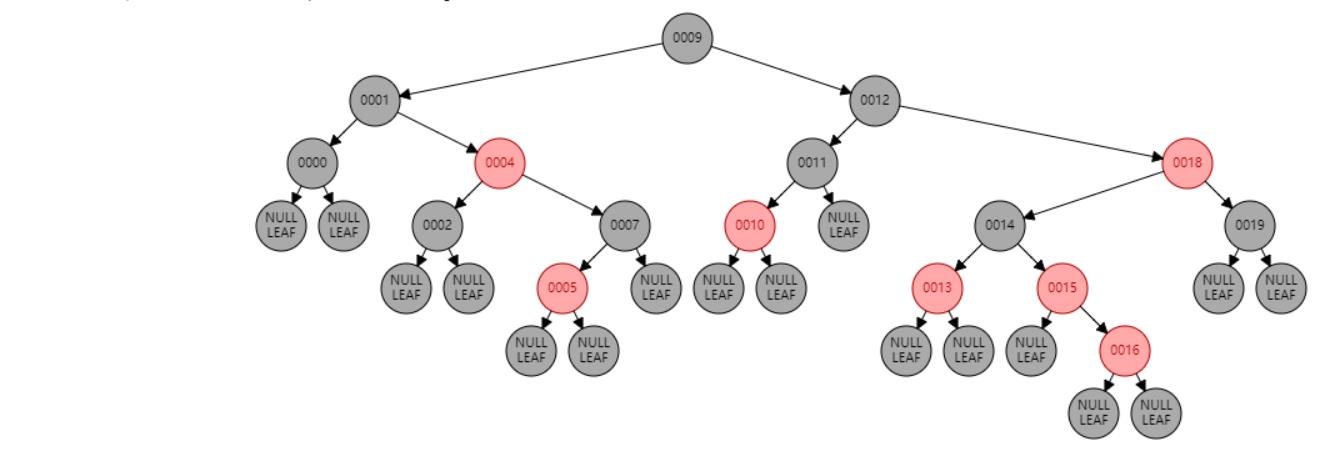
情况三：父节点P、叔叔节点U，都为红色。//祖父节点G染红色，父节点P和叔叔节点U染黑色

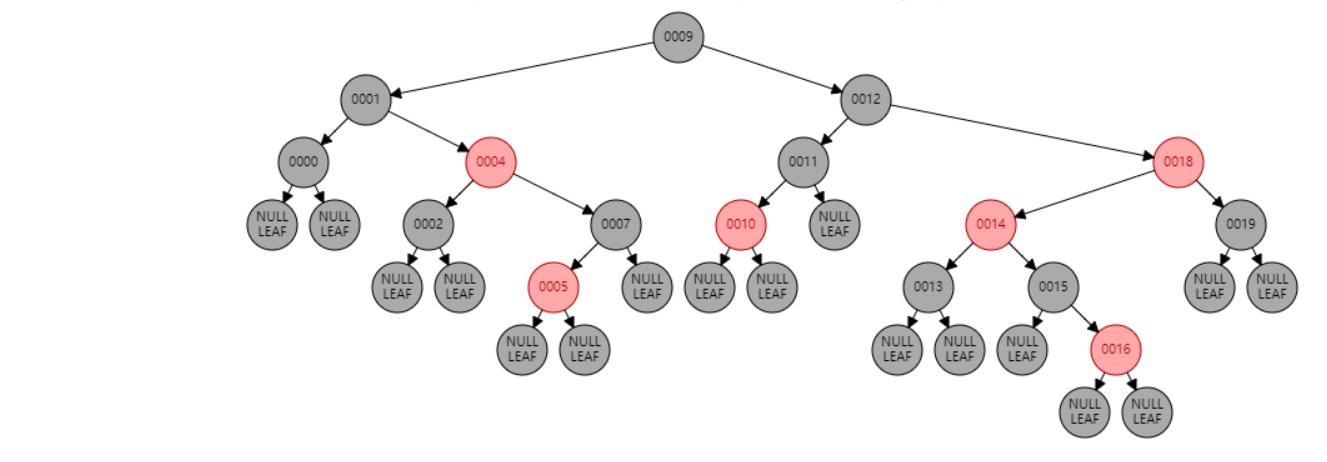
情况六：节点N和父节点P都是红色，叔叔节点U是黑色或NIL，节点N为左子节点，父节点P又是其父G的右子节点。//右旋 或 父节点P染黑色，兄弟节点B染红色

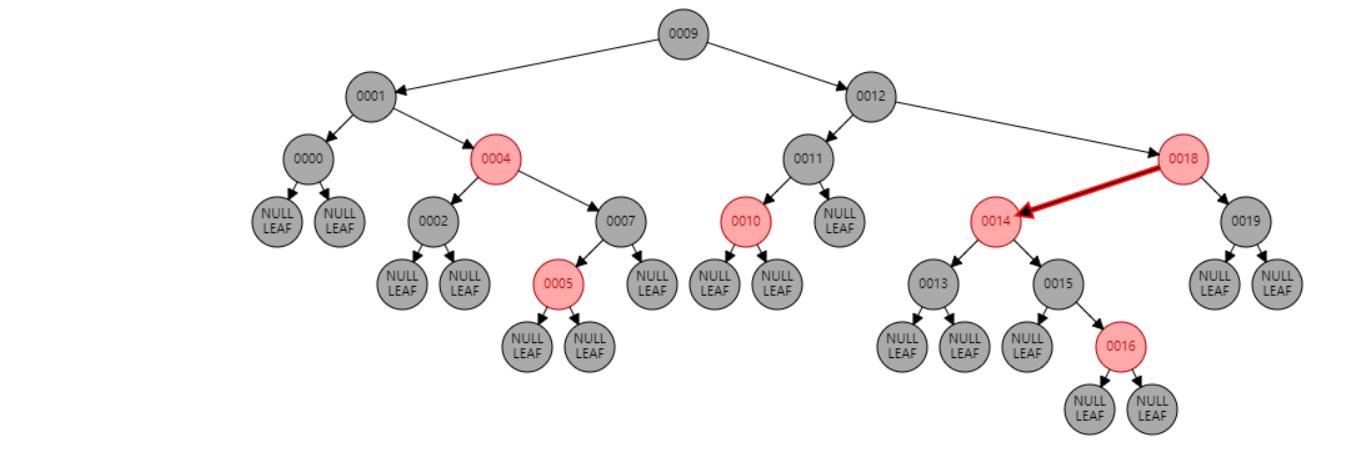
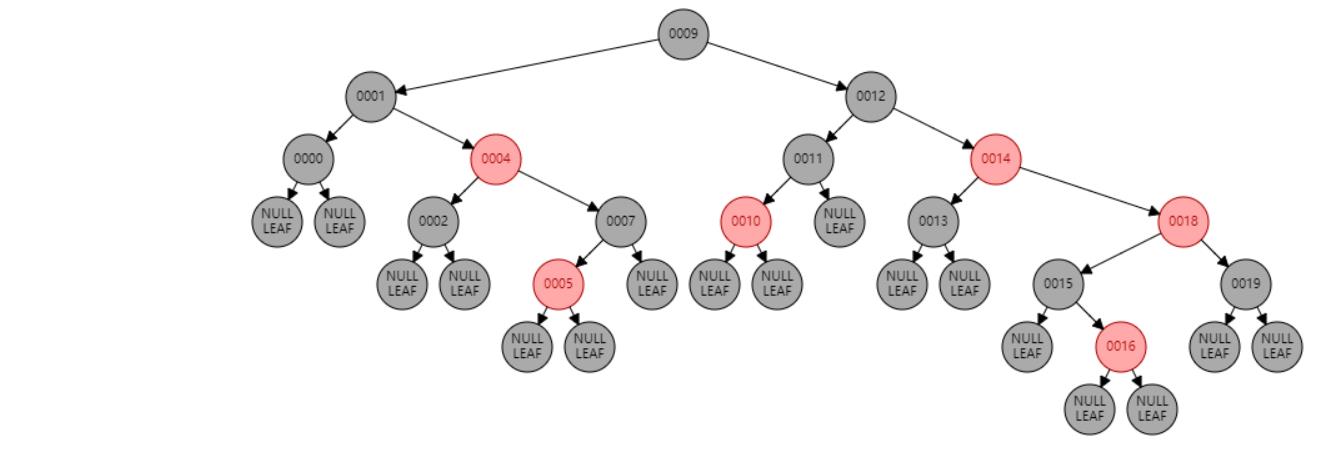
情况七：节点N和父节点P都是红色，叔叔节点U是黑色或NIL，节点N为右子节点，父节点P又是其父G的右子节点。//左旋 或 父节点P染黑色，兄弟节点B染红色

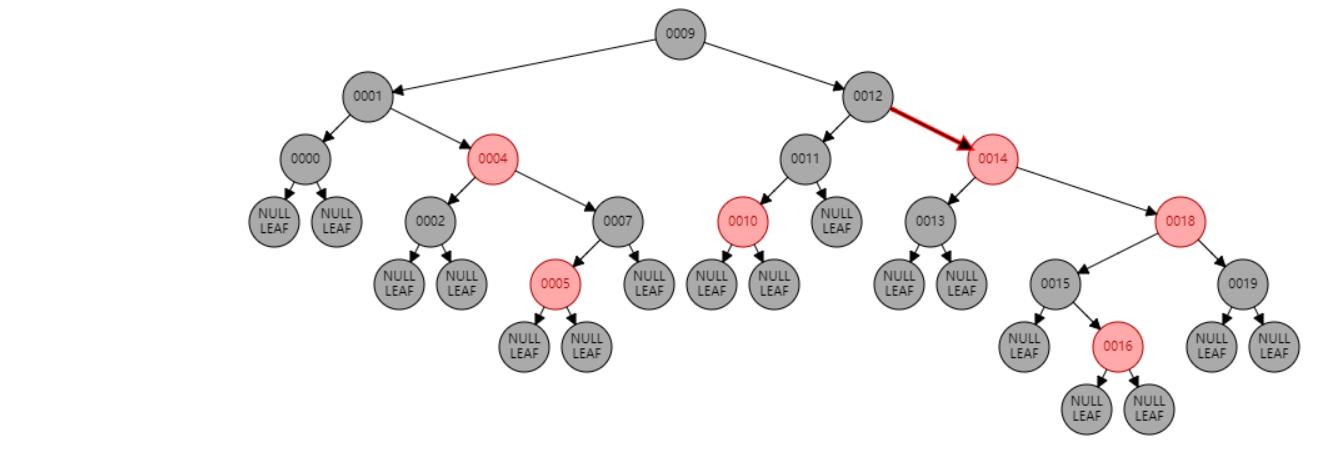
情况七：节点N和父节点P都是红色，叔叔节点U是黑色或NIL，节点N为右子节点，父节点P又是其父G的右子节点。//左旋 或 父节点P染黑色，兄弟节点B染红色

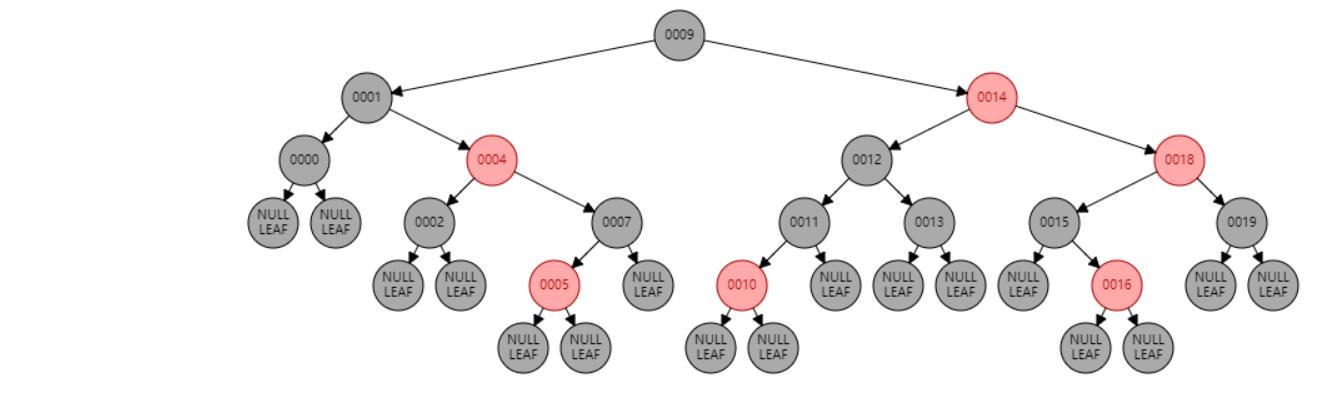
#注意，此时如果再进行旋转，最后的结果将无法满足红黑树的性质从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。树将失去平衡

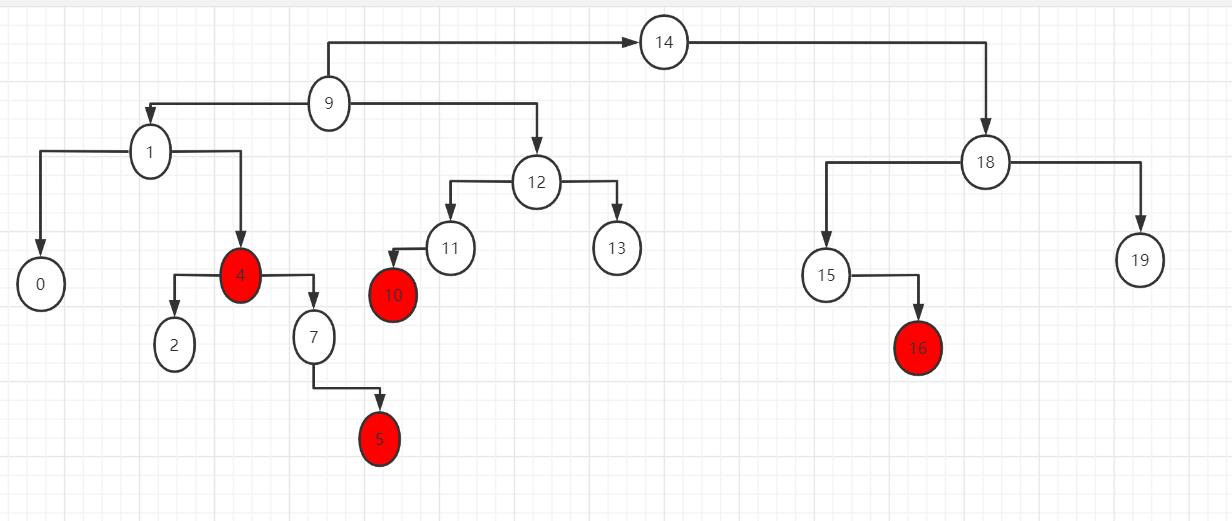
所以此时//父节点P染黑色，兄弟节点B染红色

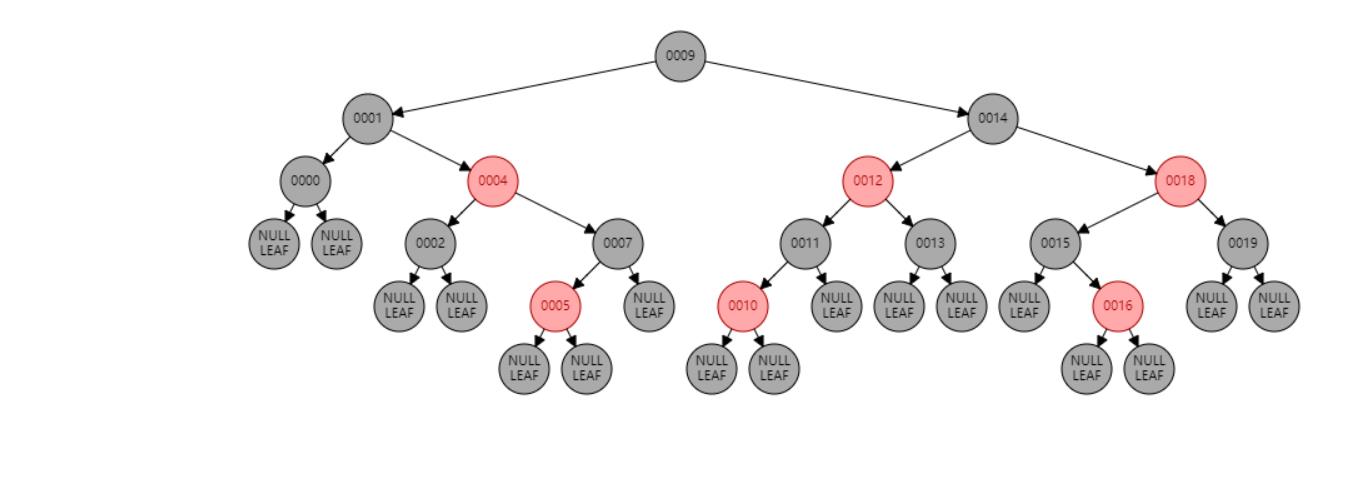
插入 6

插入节点

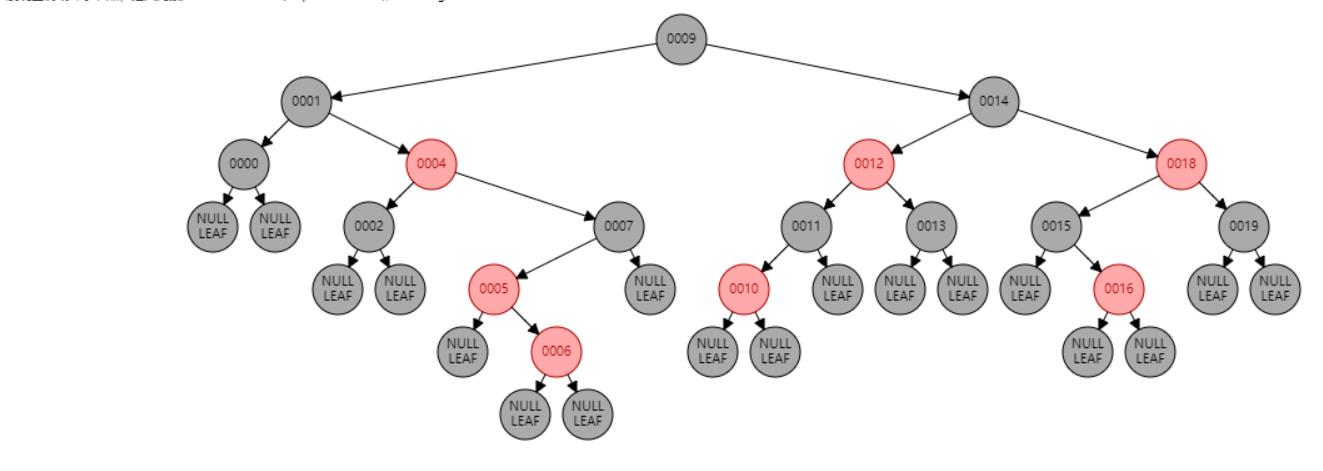
情况五：节点N和父节点P都是红色，叔叔节点U是黑色或NIL，节点N为右子节点，父节点P又是其父G的左子节点。//左旋 或 父节点P染黑色，兄弟节点B染红色

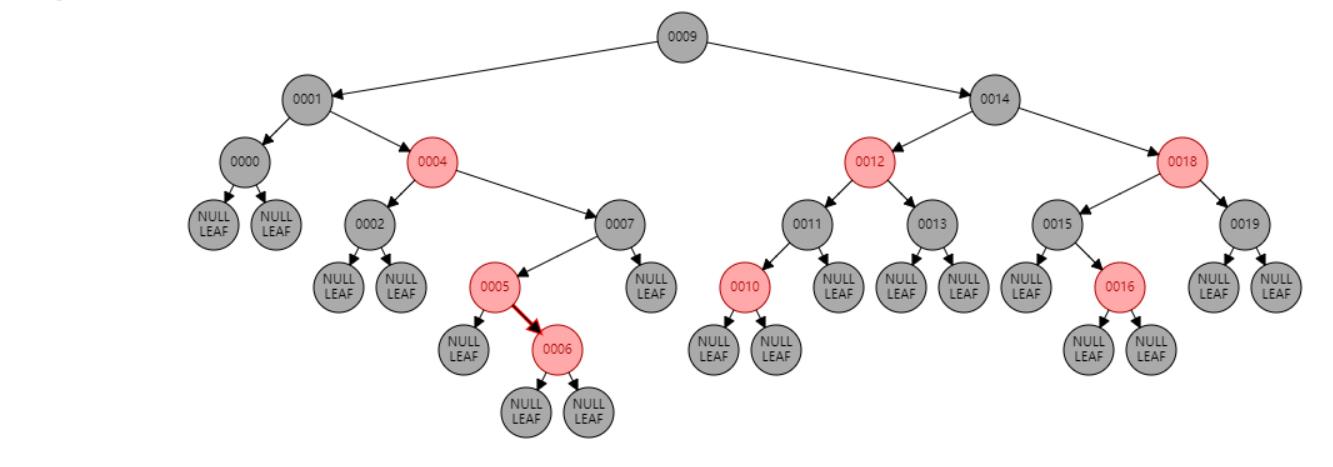
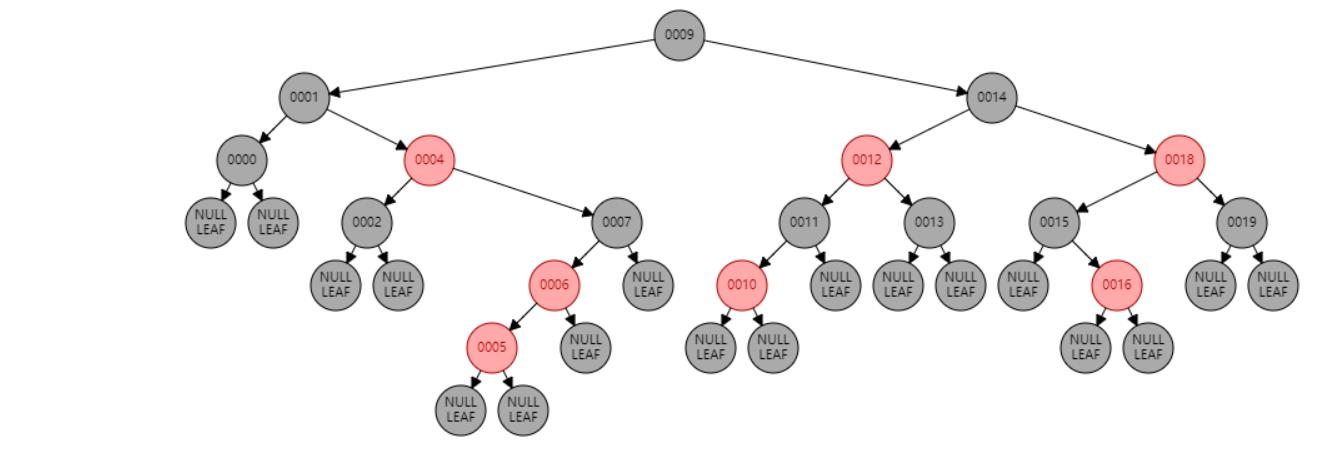
情况四：节点N和父节点P都是红色，叔叔节点U是黑色或NIL，节点N为左子节点，父节点P又是其父G的左子节点。//右旋 或 父节点P染黑色，兄弟节点B染红色

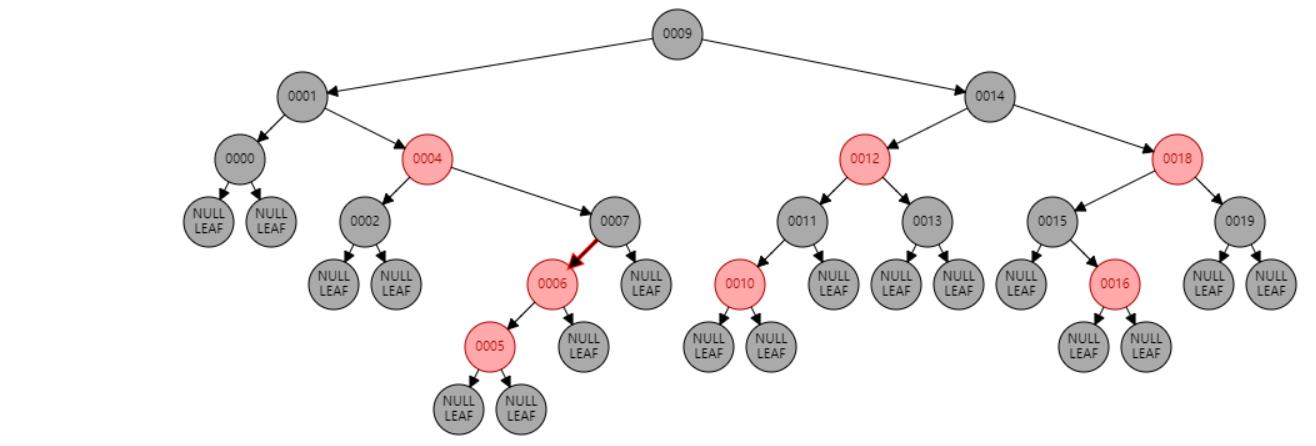
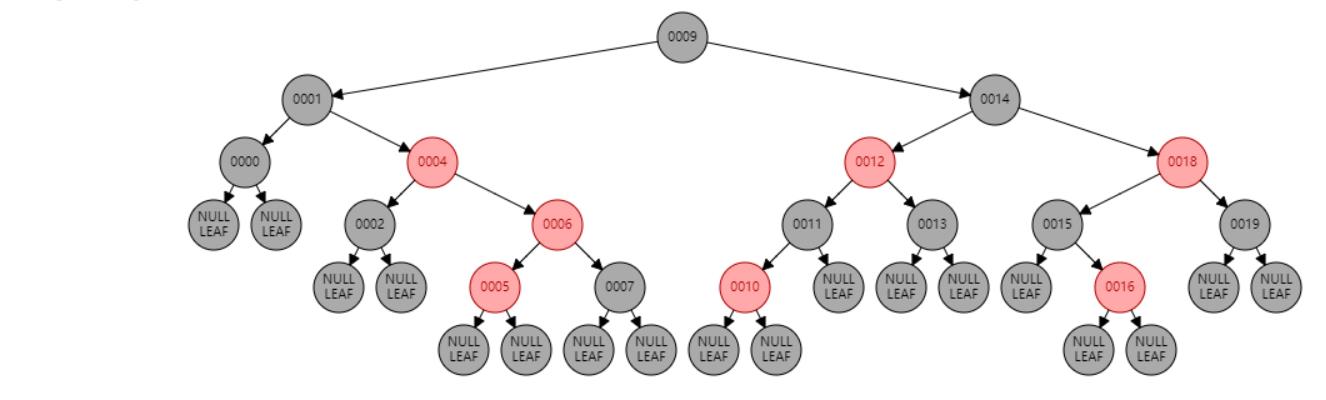
情况九：父节点P、祖父节点G，都为红色。//父节点P染黑色，兄弟节点B染红色

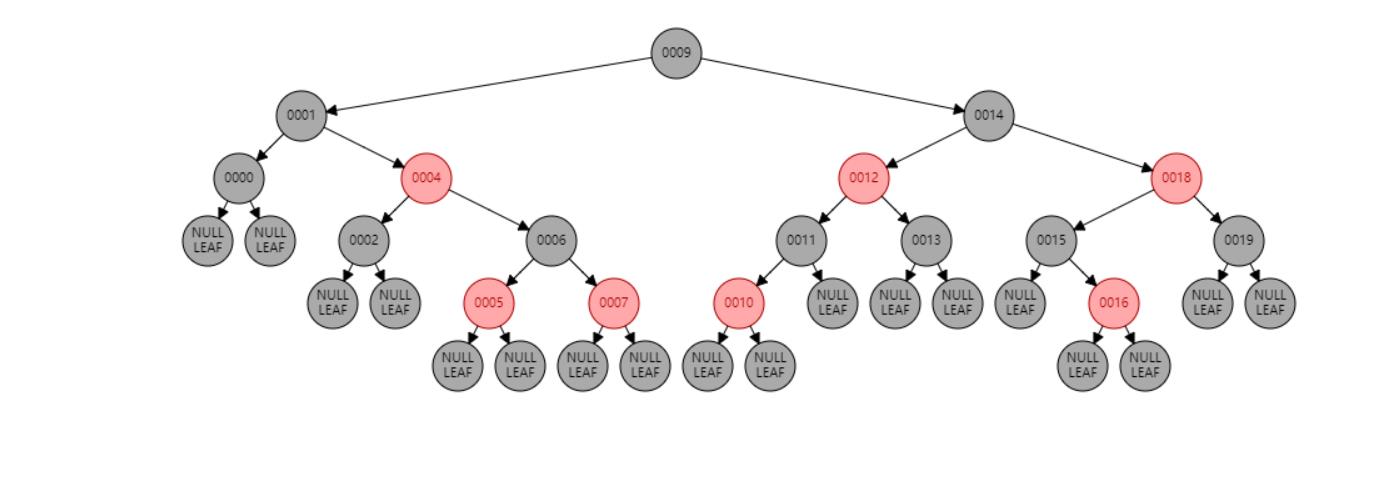
插入 3

插入节点

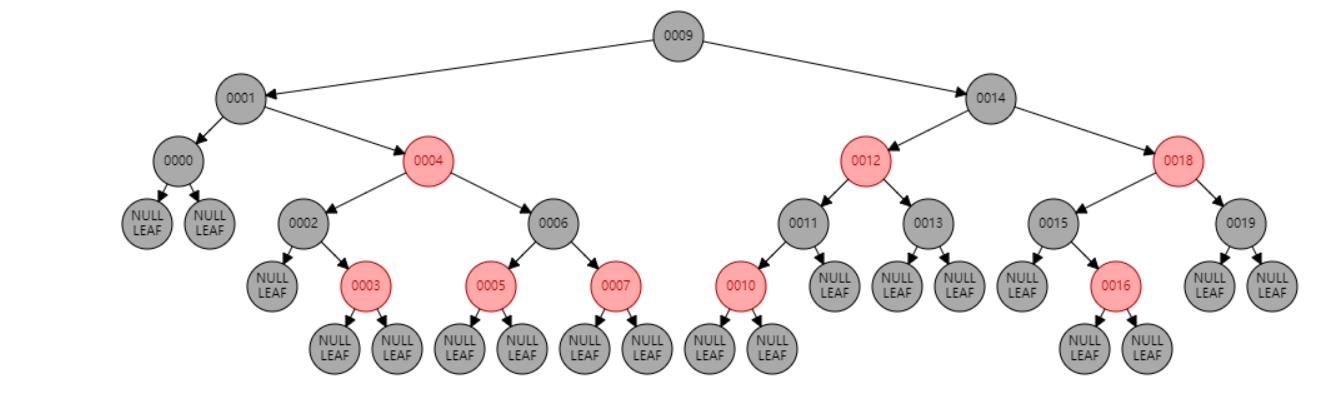
情况二：节点N的父节点P是黑色。//符合红黑树性质

插入 8

插入节点

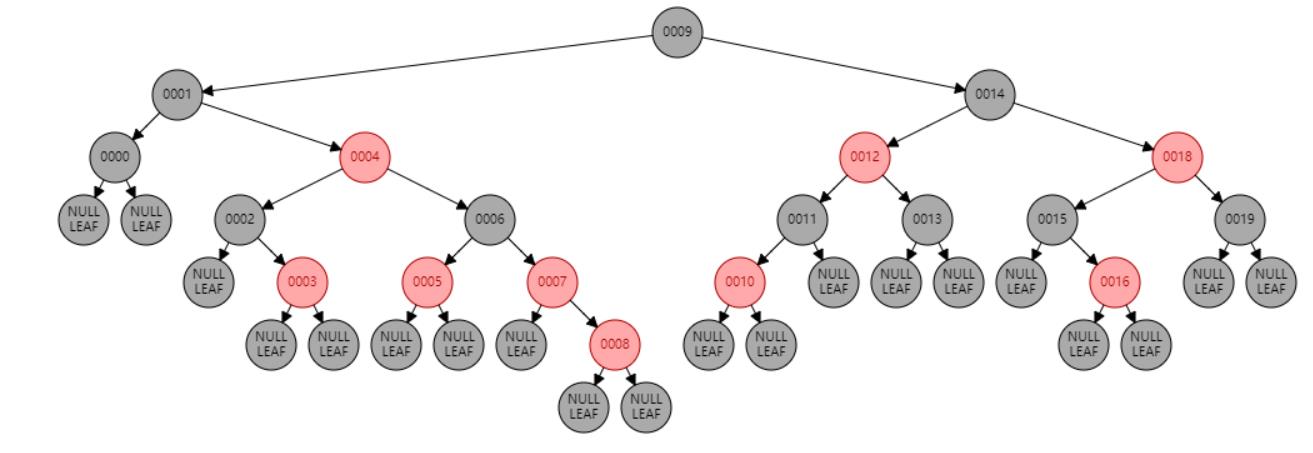
情况三：父节点P、叔叔节点U，都为红色。//祖父节点G染红色，父节点P和叔叔节点U染黑色

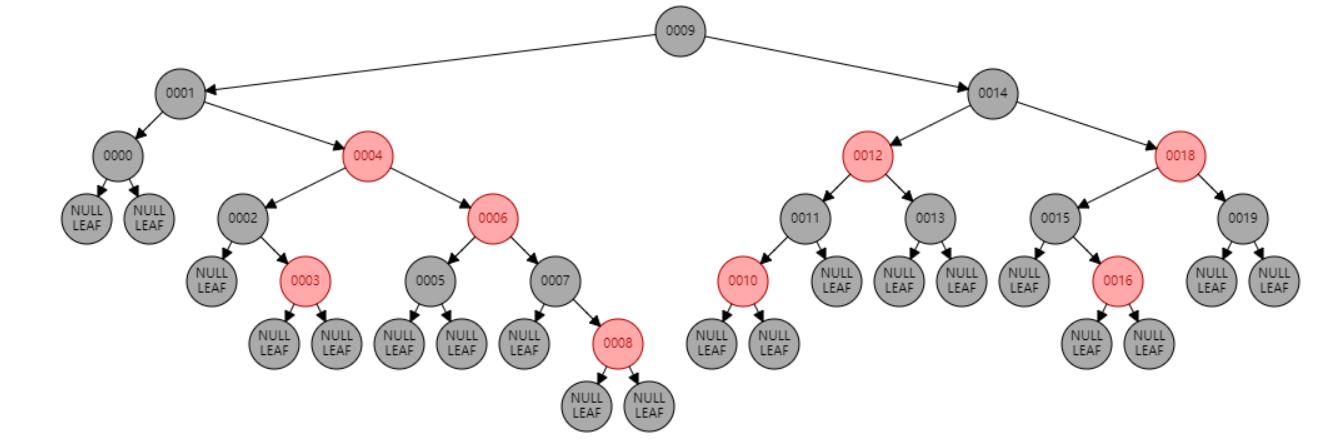
情况七：节点N和父节点P都是红色，叔叔节点U是黑色或NIL，节点N为右子节点，父节点P又是其父G的右子节点。//左旋 或 父节点P染黑色，兄弟节点B染红色

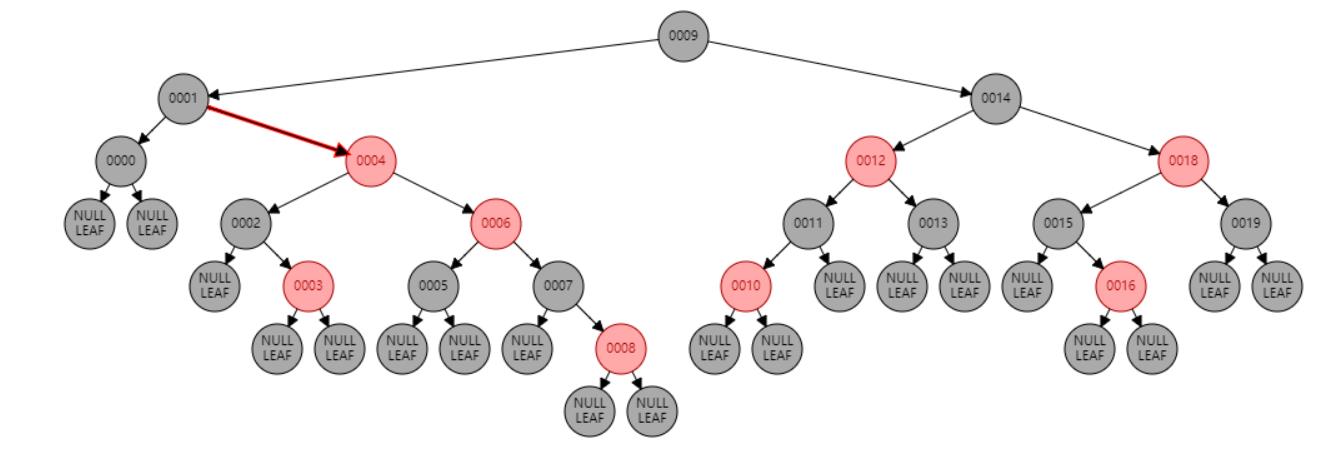
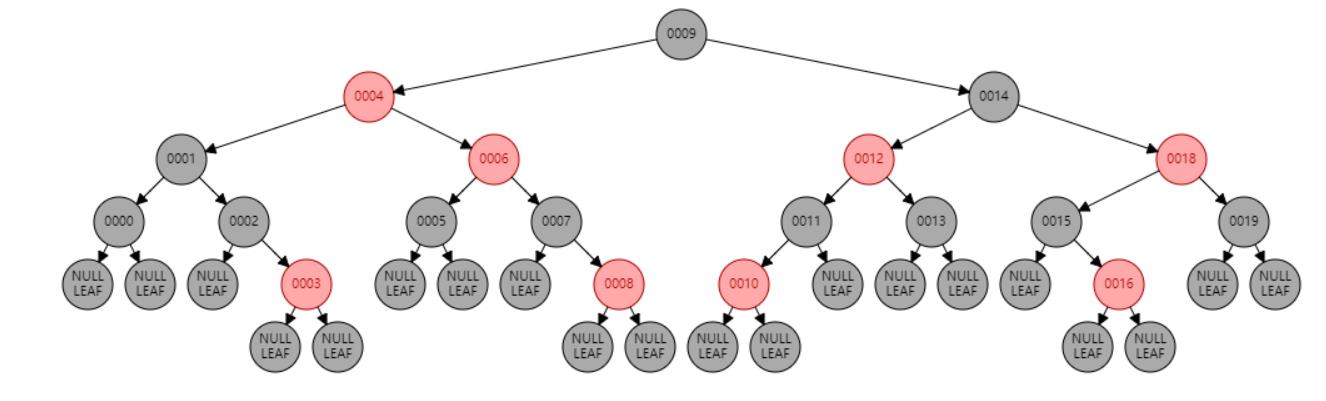
情况五：节点N和父节点P都是红色，叔叔节点U是黑色或NIL，节点N为右子节点，父节点P又是其父G的左子节点。//左旋 或 父节点P染黑色，兄弟节点B染红色

#注意，此时如果再进行旋转，最后的结果将无法满足红黑树的性质从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。树将失去平衡

所以此时//父节点P染黑色，兄弟节点B染红色

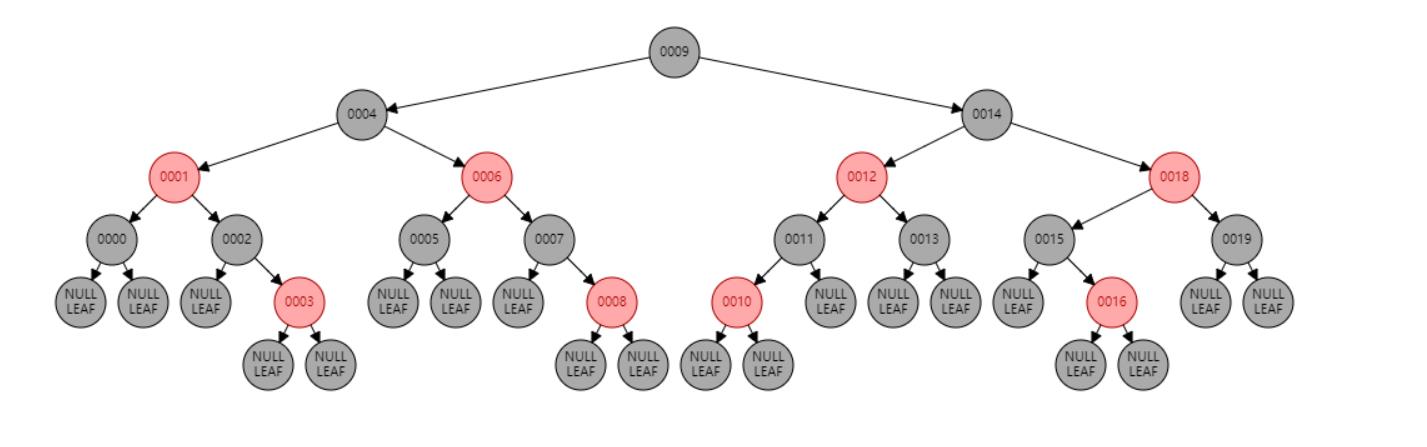
插入 17

插入节点

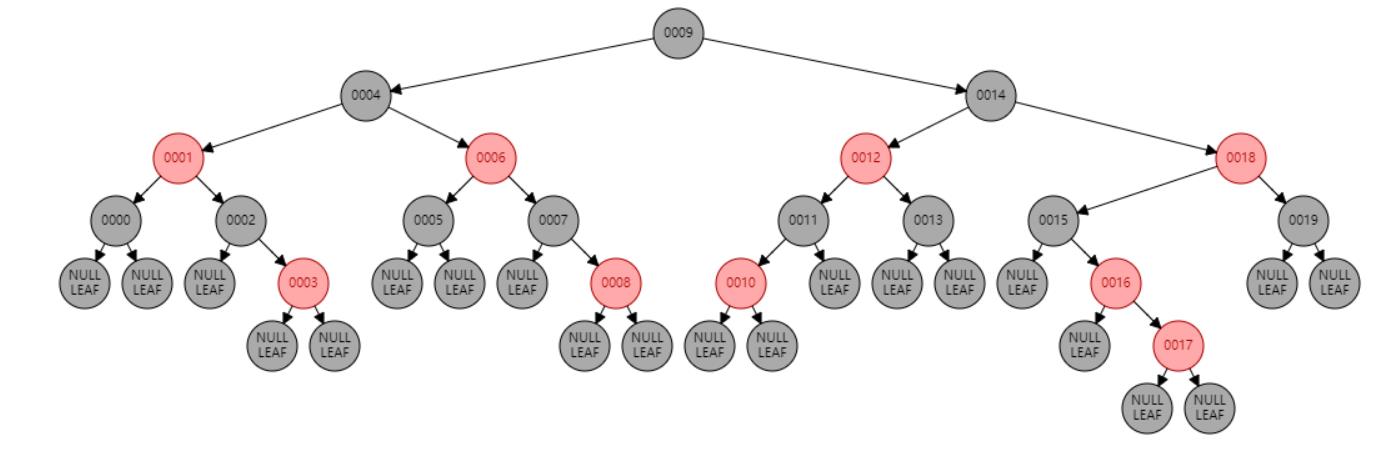
情况七：节点N和父节点P都是红色，叔叔节点U是黑色或NIL，节点N为右子节点，父节点P又是其父G的右子节点。//左旋 或 父节点P染黑色，兄弟节点B染红色

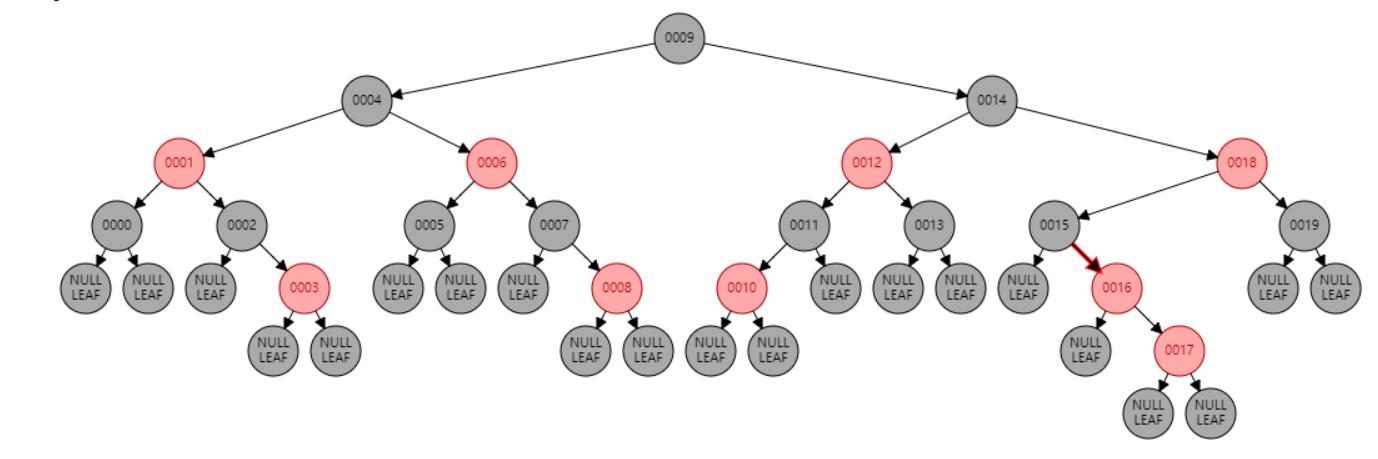
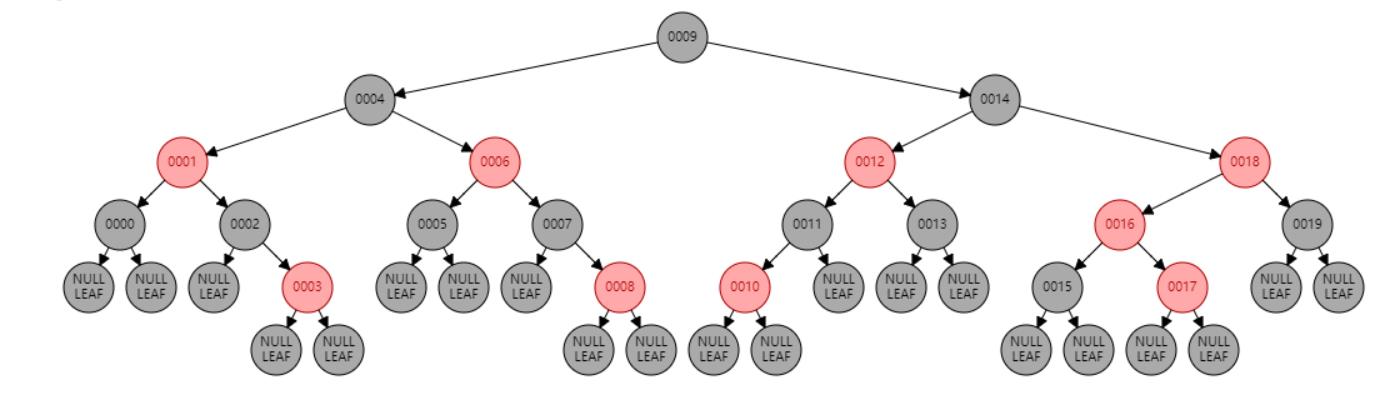
情况九：父节点P、祖父节点G，都为红色。//父节点P染黑色，兄弟节点B染红色

 

红黑树删除

红黑树的所有删除情况，如下：

1. N 是新的根。
2. 兄弟节点S是红色
3. 兄弟节点S是黑色的，且S的俩个儿子都是黑色的。但N的父节点P，是黑色。
4. 兄弟节点S 是黑色的、S 的儿子也都是黑色的，但是 N 的父亲P，是红色。
5. 兄弟S为黑色，S 的左儿子是红色，S 的右儿子是黑色，而N是它父亲的左儿子。此种情况，最后转化到下面的情况6。
6. 兄弟节点S是黑色，S的右儿子是红色，而 N 是它父亲的左儿子。

接下来，便是一一删除这些点12 1 9 2 0 11 7 19 4 15 18 5 14 13 10 16 6 3 8 17为例，即，红黑树删除情况全程演示：

各个节点删除与以上的六种情况，一一对应起来，如图：

 

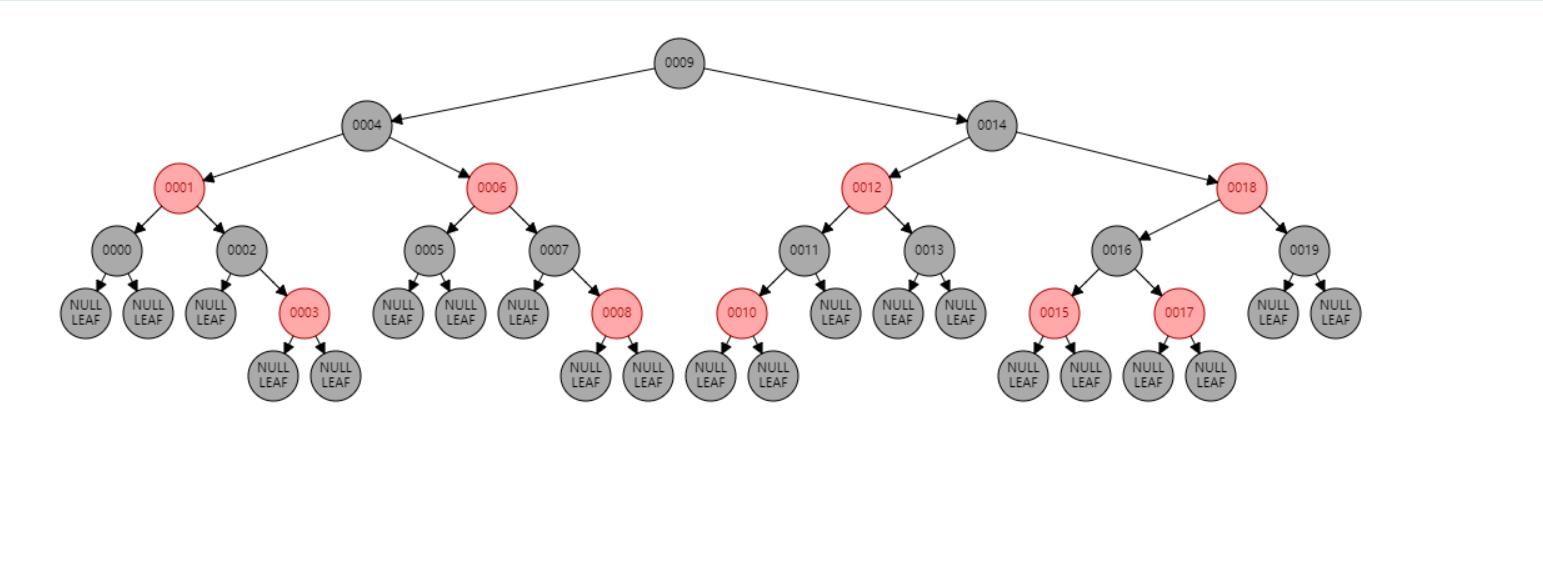
首先，插入12 1 9 2 0 11 7 19 4 15 18 5 14 13 10 16 6 3 8 17节点后，形成的红黑树为：

 

然后，以下的图片，是一一删除这些节点12 1 9 2 0 11 7 19 4 15 18 5 14 13 10 16 6 3 8 17所得到的删除情况的全程演示图：

删除 12

 

删除 1

 

删除 9

 

删除 2

 

删除 0

 

删除 11

 

删除 7

 

删除 19

 

删除 4

 

删除 15

 

删除 18

 

删除 5

 

删除 14

 

删除 13

 

删除 10

 

删除 16

 

删除 6

 

删除 3

 

删除 8

 

删除 17

 

红黑树和AVL树（平衡二叉树）的定义、特点以及两者的区别

定义

• AVL树：平衡二叉树又称AVL树，是一种特殊的二叉查找树，其左右子数都是平衡二叉树，且左右子树高度差的绝对值不超过1.一句话表述为：以树中所有结点为根的树的左右子树高度差的绝对值不超过1.将二叉树上结点的左子树深度减去右子树深度称为平衡因子BF，那么平衡二叉树上的所有结点的平衡因子只可能是-1、0和1.只要二叉树上有一个结点的平衡因子的绝对值大于1，该二叉树就是不平衡的。
• 红黑树：是一种二叉查找树，但在每个结点增加一个存储位表示结点的颜色，可以是红或者黑（非黑即红）。通过对任何一条从根到叶子的路径上各个结点着色的方式的限制，红黑树确保没有一条路径会比其他路径长出两倍，因此红黑树是一种弱平衡二叉树，相对于要求严格的AVL树来说，它的旋转次数少，所以对于搜索、插入、删除操作比较多的情况下，通常使用红黑树。

性质

红黑树的性质如下：

1. 每个结点非红即黑；
2. 根节点是黑的；
3. 每个叶节点（叶节点即树尾端NULL指针或NULL结点）都是黑的；
4. 如果一个结点是红色的，则它的子节点必须是黑色的；
5. 对于任何结点而言，其到叶子点树NULL指针的每条路径都包含相同数目的黑结点。

 

区别

区别：

• AVL树是高度平衡的，频繁的插入和删除，会引起频繁的rebalance，导致效率下降；
• 红黑树不是高度平衡的，算是一种折中，插入最多两次旋转，删除最多三次旋转。