Matlab：数模08-排队论

Posted 2021-05-18 fxalll

文章目录

• 关于排队论
• 排队系统的三要素
• 排队系统机制
• 排队论例子-01
• 排队论例子-02
• 排队论例子-03
• Matlab代码

关于排队论

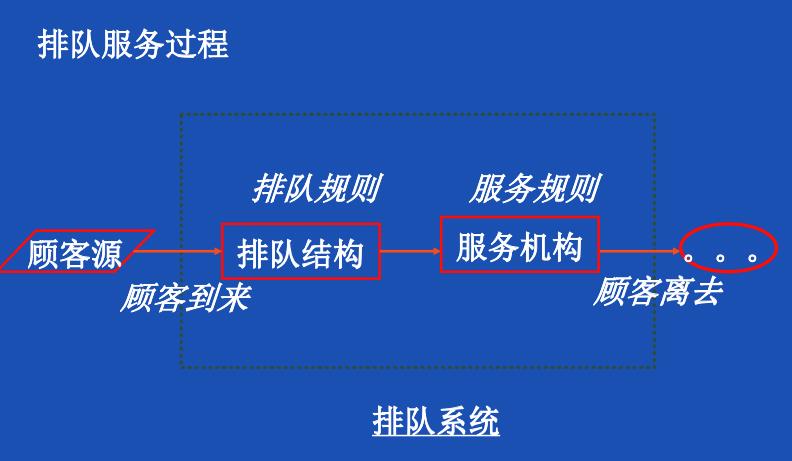
排队系统的三要素

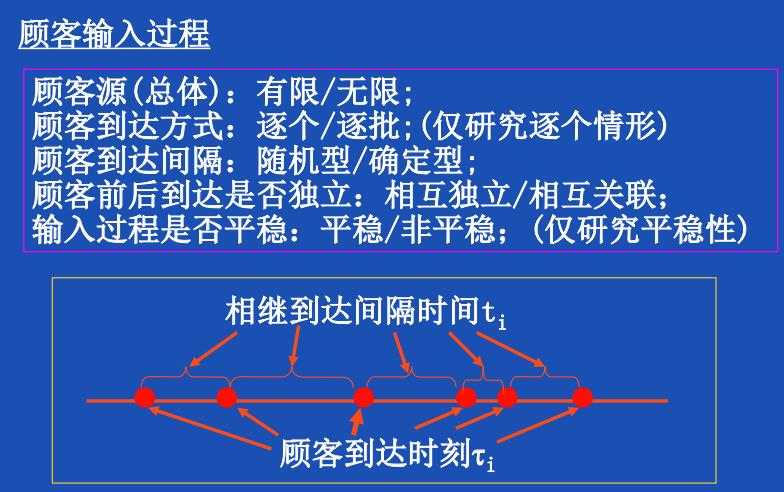
一般而言，我们研究的模型中，顾客数量总是无限、逐个、随机、相互独立、平稳的。

一般我们研究的是禁止退出和转移。什么意思呢？比如你去麦当劳排队，你看到旁边的人更少，你就会到那边的队伍去；又或者你等太久了决定不排了走了。这在我们的模型是不考虑的。

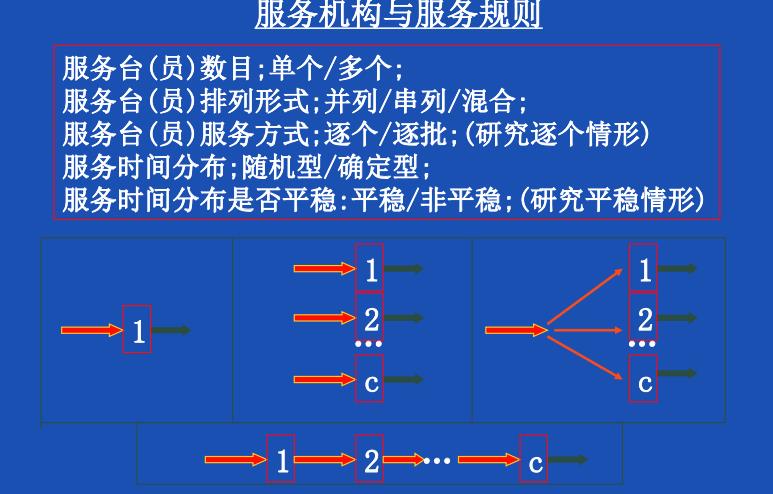
排队系统机制

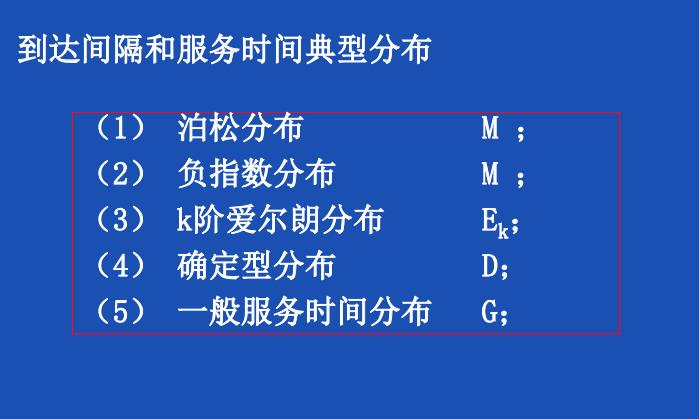
评价排队系统的优劣是我们所关注的。

逗留时间也是我们在模型中关注的变量。

λ为单位时间到达系统的人数；μ为服务台单位时间能处理的人数；s为服务台个数。


一般可以认为顾客到达的都是柏松流的。

排队论例子-01

排队论例子-02

排队论例子-03

以例三为例，我们可以使用Matlab进行编程。

Matlab代码

s=3;
mu=24;
lambda=54;
ro=lambda/mu;
ros=ro/s;
sum1=0;

for i=0:(s-1)
    sum1=sum1+ro.^i/factorial(i);
end

sum2=ro.^s/factorial(s)/(1-ros);

p0=1/(sum1+sum2);
p=ro.^s.*p0/factorial(s)/(1-ros);
Lq=p.*ros/(1-ros);
L=Lq+ro;
W=L/lambda;
Wq=Lq/lambda;
fprintf('排队等待的平均人数为%5.2f人\\n',Lq)
fprintf('系统内的平均人数为%5.2f人\\n',L)
fprintf('平均逗留时间为%5.2f分钟\\n',W*60)
fprintf('平均等待时间为%5.2f分种\\n',Wq*60)

其中s为服务台数=3，mu为一个服务台平均每小时服务人数为0。4*60=24，lambda为平均每小时到达人数为0.9*60=54。

以上代码保存为paidui01.m并运行。

可以看出与例子计算结果是一样的。

我们还可以使用以下代码进行编程，与例三无关，大家可以自己尝试一下：

clear 
clc 
%***************************************** 
%初始化顾客源 
%***************************************** 
%总仿真时间 
Total_time = 10; 
%队列最大长度 
N = 10000000000; 
%到达率与服务率 
lambda = 10; 
mu = 6; 
%平均到达时间与平均服务时间 
arr_mean = 1/lambda; 
ser_mean = 1/mu; 
arr_num = round(Total_time*lambda*2); 
events = []; 
%按负指数分布产生各顾客达到时间间隔 
events(1,:) = exprnd(arr_mean,1,arr_num); 
%各顾客的到达时刻等于时间间隔的累积和 
events(1,:) = cumsum(events(1,:)); 
%按负指数分布产生各顾客服务时间 
events(2,:) = exprnd(ser_mean,1,arr_num); 
%计算仿真顾客个数，即到达时刻在仿真时间内的顾客数 
len_sim = sum(events(1,:)<= Total_time); 
%***************************************** 
%计算第 1个顾客的信息 
%***************************************** 
%第 1个顾客进入系统后直接接受服务，无需等待 
events(3,1) = 0; 
%其离开时刻等于其到达时刻与服务时间之和 
events(4,1) = events(1,1)+events(2,1); 
%其肯定被系统接纳，此时系统内共有 
%1个顾客，故标志位置1 
events(5,1) = 1; 
%其进入系统后，系统内已有成员序号为 1 
member = [1]; 
for i = 2:arr_num 
%如果第 i个顾客的到达时间超过了仿真时间，则跳出循环 

if events(1,i)>Total_time 

break; 

else 
number = sum(events(4,member) > events(1,i)); 
%如果系统已满，则系统拒绝第 i个顾客，其标志位置 0 
if number >= N+1 
events(5,i) = 0; 
%如果系统为空，则第 i个顾客直接接受服务 
else 
if number == 0 
%其等待时间为 0

2009.1516

%PROGRAMLANGUAGEPROGRAMLANGUAGE
events(3,i) = 0; 
%其离开时刻等于到达时刻与服务时间之和 
events(4,i) = events(1,i)+events(2,i); 
%其标志位置 1 
events(5,i) = 1; 
member = [member,i]; 
%如果系统有顾客正在接受服务，且系统等待队列未满，则 第 i个顾客进入系统 

else len_mem = length(member); 
%其等待时间等于队列中前一个顾客的离开时刻减去其到 达时刻 
events(3,i)=events(4,member(len_mem))-events(1,i); 
%其离开时刻等于队列中前一个顾客的离开时刻加上其服 
%务时间 
events(4,i)=events(4,member(len_mem))+events(2,i); 
%标识位表示其进入系统后，系统内共有的顾客数 
events(5,i) = number+1; 
member = [member,i]; 
end 
end 

end 
end 
%仿真结束时，进入系统的总顾客数 
len_mem = length(member); 
%***************************************** 
%输出结果 
%***************************************** 
%绘制在仿真时间内，进入系统的所有顾客的到达时刻和离 
%开时刻曲线图（stairs：绘制二维阶梯图） 
stairs([0 events(1,member)],0:len_mem); 
hold on; 
stairs([0 events(4,member)],0:len_mem,'.-r'); 
legend('到达时间 ','离开时间 '); 
hold off; 
grid on; 
%绘制在仿真时间内，进入系统的所有顾客的停留时间和等 
%待时间曲线图（plot：绘制二维线性图） 
figure; 
plot(1:len_mem,events(3,member),'r-*',1: len_mem,events(2,member)+events(3,member),'k-'); 
legend('等待时间 ','停留时间 '); 
grid on;

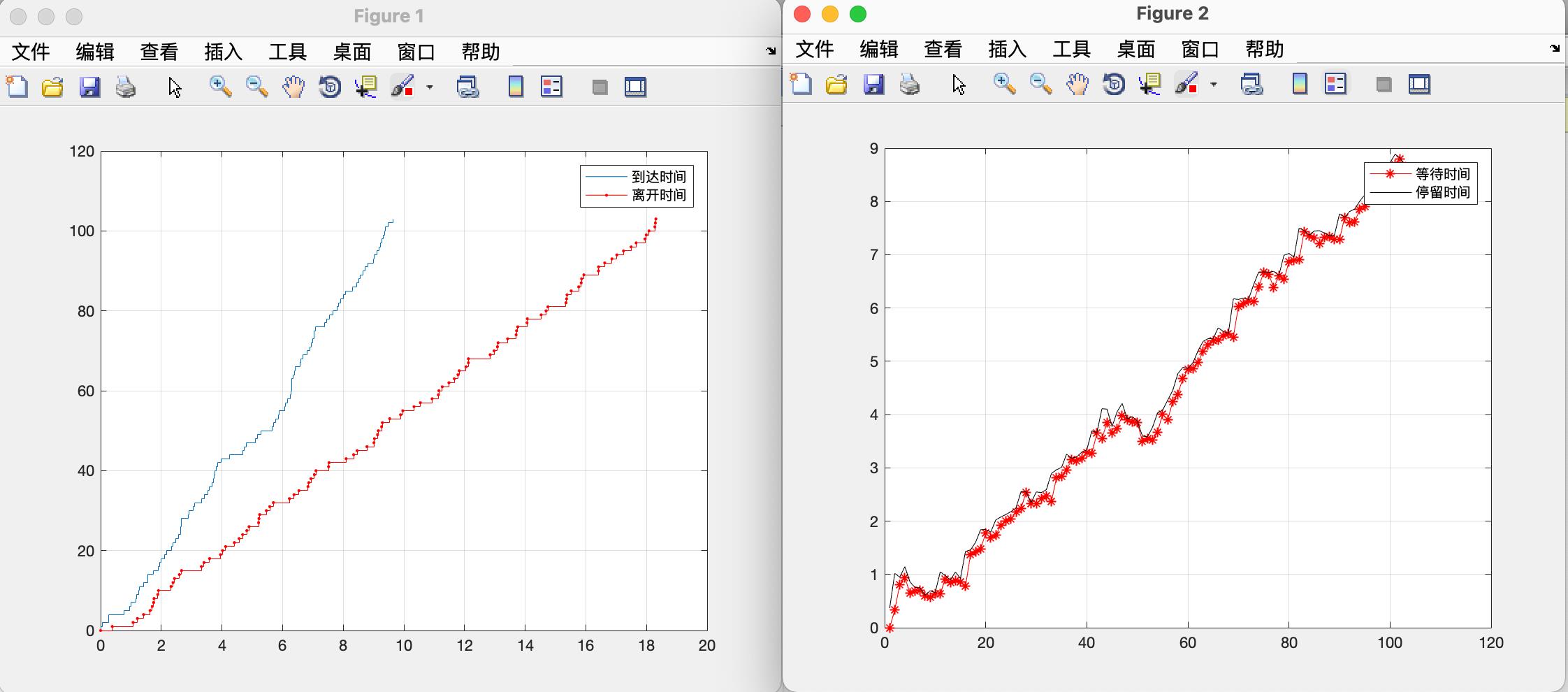
首先观察图Figure1，蓝色为到达时间，红色为离开时间。设置的模拟时间为10，所以在10个单位的时间内到达了100多个人。而一个人的总停留时间多少便是x轴方向蓝线与红线的距离大小。可以看出越往后，等待的时间越长。

图Figure2，停留时间 - 等待时间 = 服务时间。

我们修改代码加深理解：

我们将服务率提高到10，再看看：

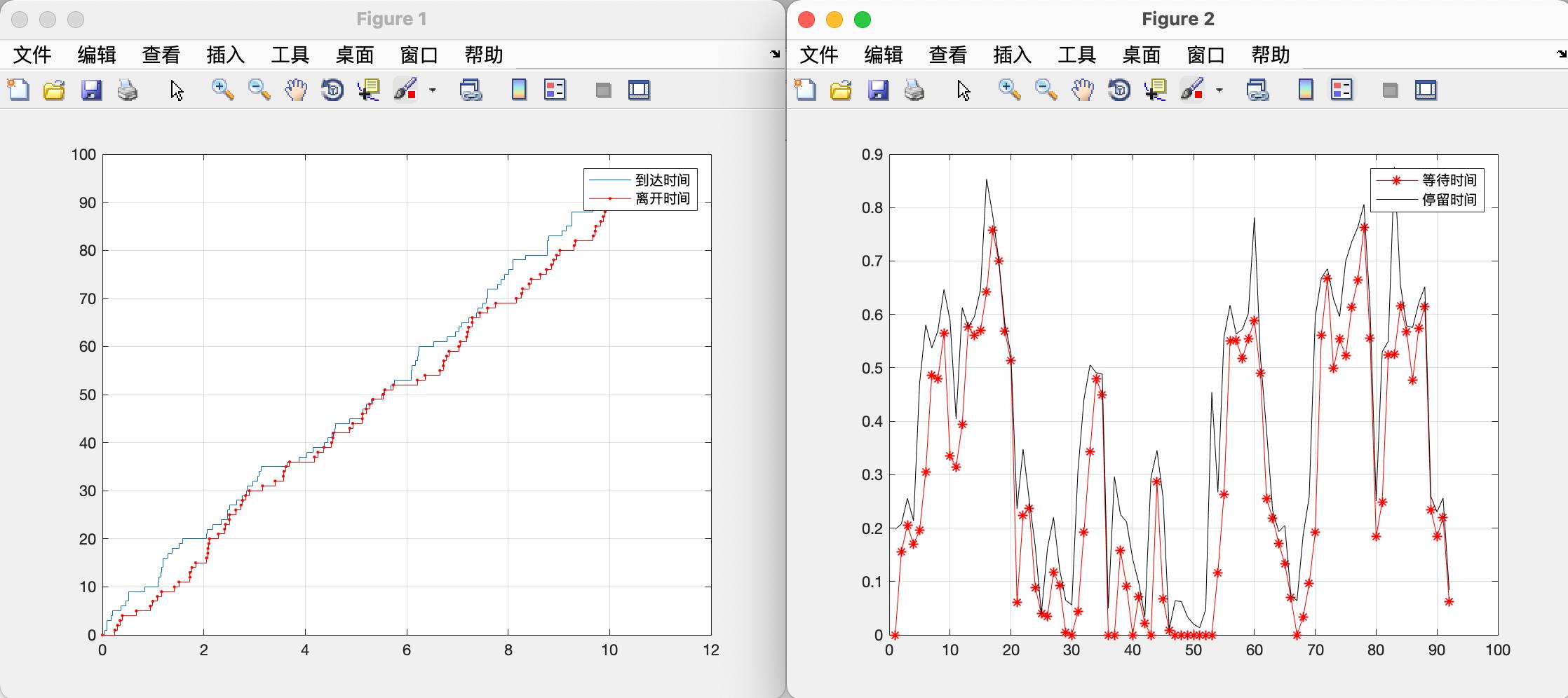
可以看出顾客等待时间大幅度下降，随着时间流逝，后面顾客的等待时间不会明显增加。