Matlab：数模04-图论模型（dijstra算法）

Posted 2021-05-18 fxalll

文章目录

• 一个简单的例子
• dijstra算法简介与例子计算
• 带权邻接矩阵
• Matlab代码
• 代码测试

一个简单的例子

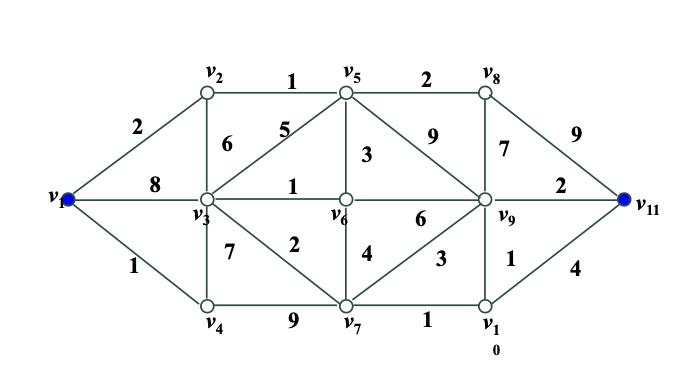
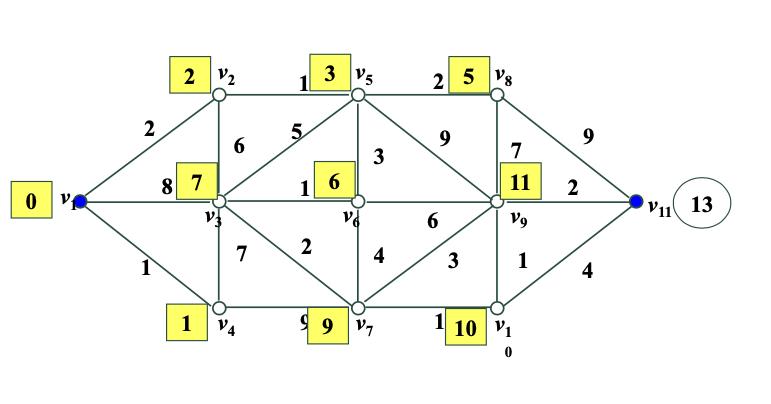
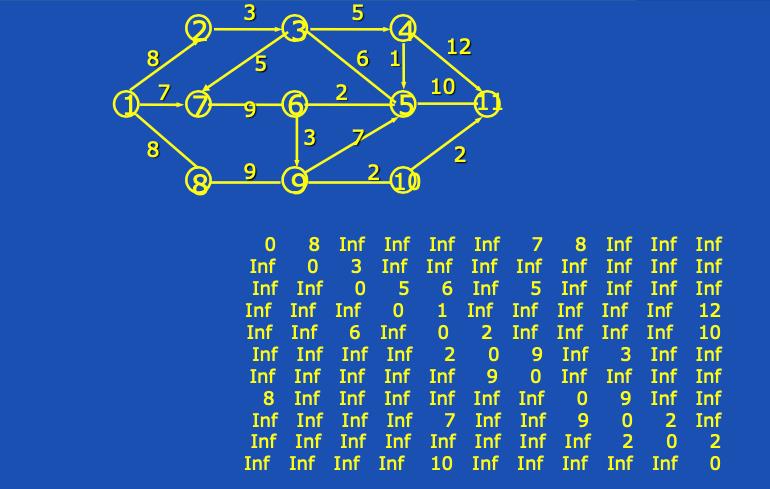
假设每个数字代表的都是点与点之间的距离。我们从v1出发，v11为终点。要如何走才能使路程最短？

dijstra算法简介与例子计算

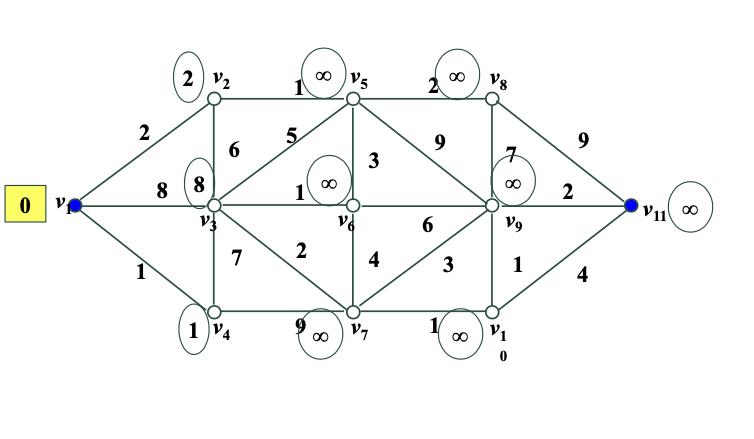
首先先写出各点距离v1的距离，然后走最短距离的那个点。

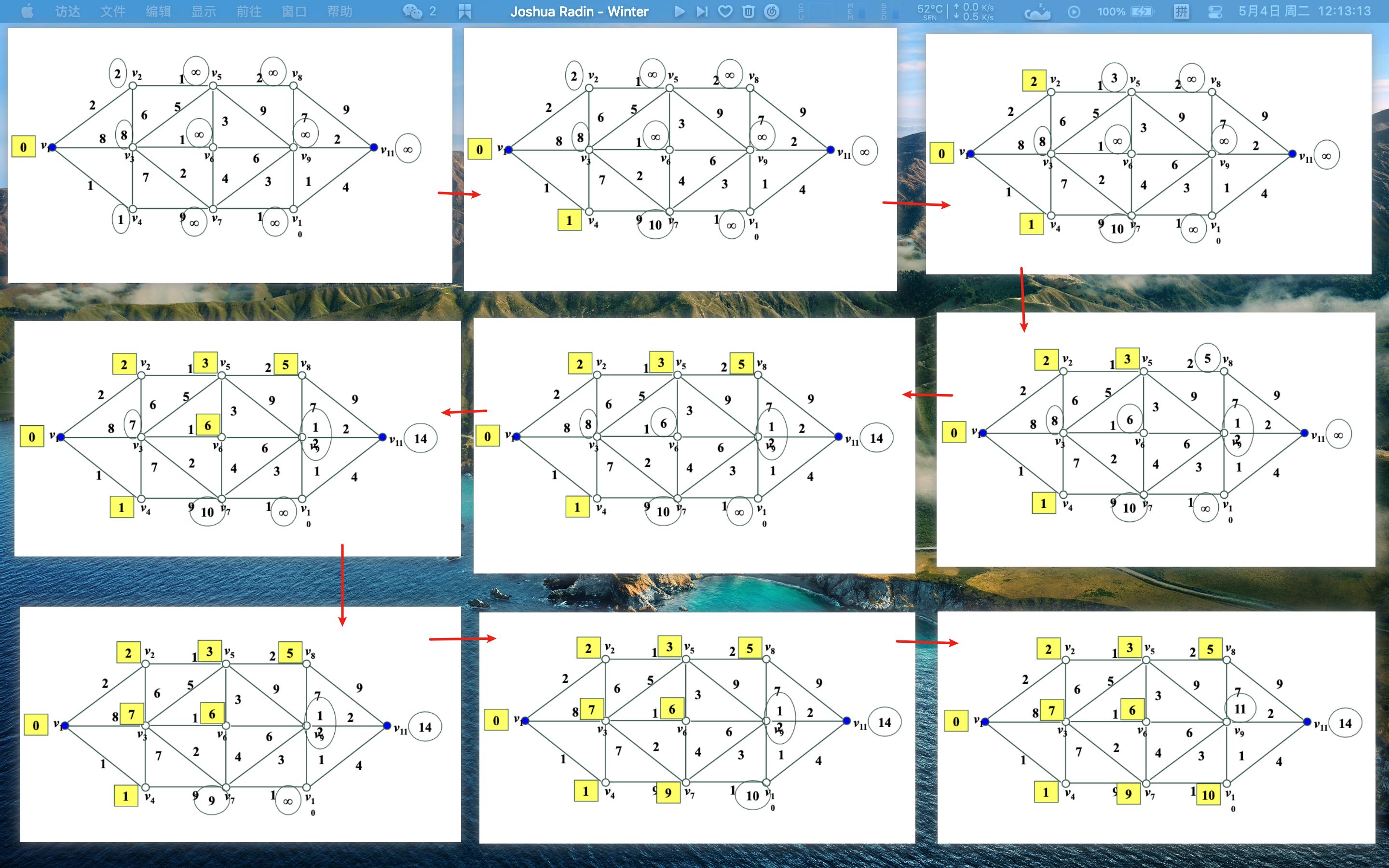
第二步走到v4，得到v1到v3、v7的距离，比较后决定第二步走v2，得到v1到v3、v5的距离，找最短距离。

第三步走到v5，得到v1到v3、v6、v8、v9的距离，找最短距离。

第四步走到v8，得到v1到v9、v11的距离。我们发现距离都挺长的，于是我们尝试回到v6，得到v1到v3、v7、v9的距离，找最短距离。

第五步走到v3，得到v1到v4、v7的距离，找最短距离。

第六步走到v7，得到v1到v9、v10的距离，找最短距离。

第七步走到v10，得到v1到v9、v11的距离，找最短距离。

第八步走到v9，直接走到v11。

以下为步骤图形化：

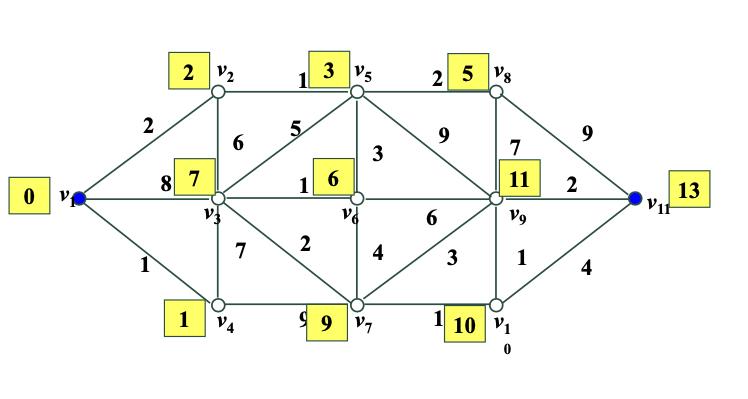
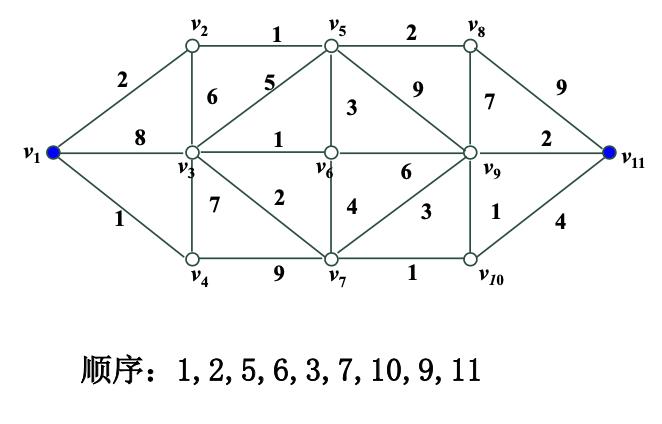
但是一旦路线复杂，这样的问题靠人力思考是很难的。我们于是使用Matlab解决这个问题。在使用Matlab之前，我们先引出一个概念，带权邻接矩阵。

带权邻接矩阵

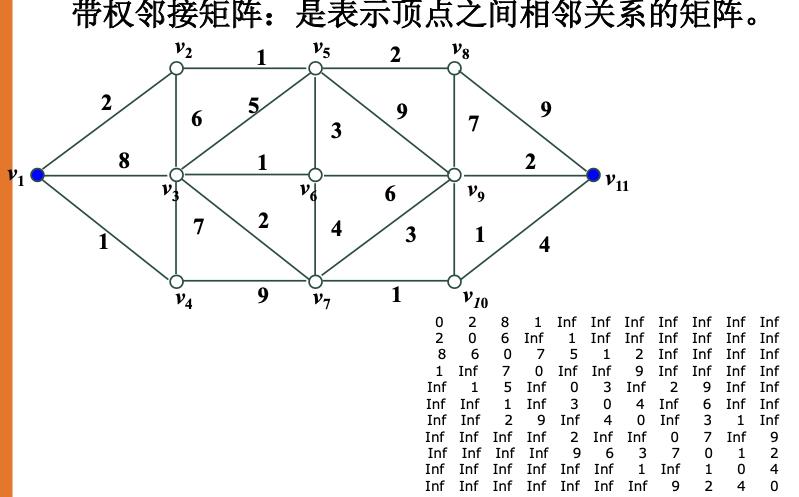
这里的数字，比如首行首列的0，为v1到v1距离。首行第二列的2，为v1到v2的距离。以此类推。

当然，也有单箭头单向模式。

有了这些积累，我们就可以使用Matlab进行编程了。

Matlab代码

function [min,path]=dijkstra(w,start,terminal)
n=size(w,1); label(start)=0; f(start)=start;
for i=1:n
   if i~=start
       label(i)=inf;
end, end
s(1)=start; u=start;
while length(s)<n
   for i=1:n
      ins=0;
      for j=1:length(s)
         if i==s(j)
            ins=1;
         end,  
      end
      if ins==0
         v=i;
         if label(v)>(label(u)+w(u,v))
            label(v)=(label(u)+w(u,v)); 
         f(v)=u;
         end, 
      end, 
   end   
v1=0;
   k=inf;
   for i=1:n
         ins=0;
         for j=1:length(s)
            if i==s(j)
               ins=1;
            end, 
         end
         if ins==0
            v=i;
            if k>label(v)
               k=label(v);  v1=v;
            end,  
         end,  
   end
   s(length(s)+1)=v1;  
   u=v1;
end
min=label(terminal); path(1)=terminal;
i=1; 
while path(i)~=start
      path(i+1)=f(path(i));
      i=i+1 ;
end
path(i)=start;
L=length(path);
path=path(L:-1:1);

我们先将以上代码保存命名为“dijkstra.m”，然后再新建一个脚本输入以下代码：

weight=    [0     2     8     1   Inf   Inf   Inf   Inf   Inf   Inf   Inf;
            2     0     6   Inf     1   Inf   Inf   Inf   Inf   Inf   Inf;
            8     6     0     7     5     1     2   Inf   Inf   Inf   Inf;
            1   Inf     7     0   Inf   Inf     9   Inf   Inf   Inf   Inf;
          Inf     1     5   Inf     0     3   Inf     2     9   Inf   Inf;
          Inf   Inf     1   Inf     3     0     4   Inf     6   Inf   Inf;
          Inf   Inf     2     9   Inf     4     0   Inf     3     1   Inf;
          Inf   Inf   Inf   Inf     2   Inf   Inf     0     7   Inf     9;
          Inf   Inf   Inf   Inf     9     6     3     7     0     1     2;
          Inf   Inf   Inf   Inf   Inf   Inf     1   Inf     1     0     4;
          Inf   Inf   Inf   Inf   Inf   Inf   Inf     9     2     4     0;];
[dis, path]=dijkstra(weight,1, 11)

可将其保存为“tulun.m”。

修改时我们仅需修改tulun.m内的代码中的变量weight以及最下角的1和11这三个。weight的编写参照上文的“带权邻接矩阵”，1代表从v1开始，11代表从v11结束。

代码测试

我们只需要在命令行输入“tulun”即可快速得到结果。

dis为最短距离，path为经过的编号。