图像识别基于BP神经网络的手写字体识别matlab源码

Posted 2021-05-18 Matlab走起

一、感知器（机）

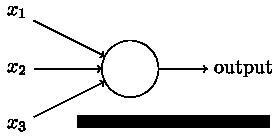
  上图的圆圈就代表一个感知器。它接受多个输入（x1，x2，x3…），产生一个输出（output），好比神经末梢感受各种外部环境的变化，最后产生电信号。

  为了简化模型，我们约定每种输入只有两种可能：1 或 0。如果所有输入都是1，表示各种条件都成立，输出就是1；如果所有输入都是0，表示条件都不成立，输出就是0。

  对于输入信号，它们对于输出信号的重要性是不一样的，这种重要性可以用权值来描述。这时，还需要指定一个阈值（threshold）。如果总和大于阈值，感知器输出1，否则输出0。假定阈值为8，那么 12 > 8，小明决定去参观。阈值的高低代表了意愿的强烈，阈值越低就表示越想去，越高就越不想去。

  上面的决策过程，使用数学表达如下：

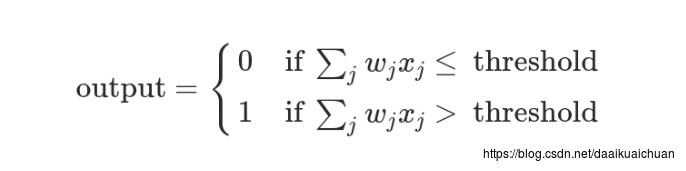
上面公式中，x表示各种外部因素，w表示对应的权重。

二、神经网络

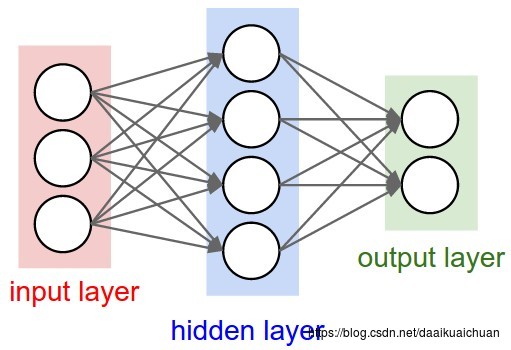
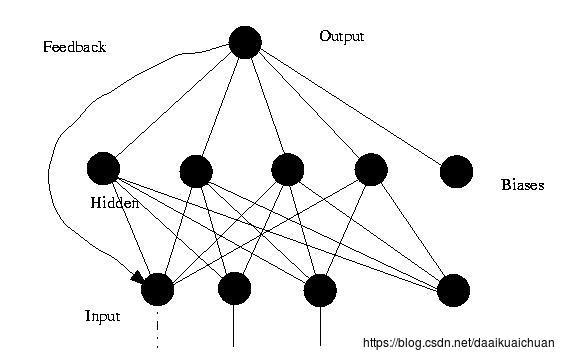
  神经网络其实就是按照一定规则连接起来的多个神经元。下图展示了一个全连接(full connected, FC)神经网络：

1、神经网络的特点

1. 神经元按照层来布局。最左边的层叫做输入层，负责接收输入数据；最右边的层叫输出层，我们可以从这层获取神经网络输出数据。输入层和输出层之间的层叫做隐藏层，因为它们对于外部来说是不可见的；

2. 同一层的神经元之间没有连接；

3. 第N层的每个神经元和第N-1层的所有神经元相连(这就是full connected的含义)，第N-1层神经元的输出就是第N层神经元的输入；

4. 每个连接都有一个权值。

上面这些规则定义了全连接神经网络的结构。事实上还存在很多其它结构的神经网络，比如卷积神经网络(CNN)、循环神经网络(RNN)，他们都具有不同的连接规则。

2、激活函数

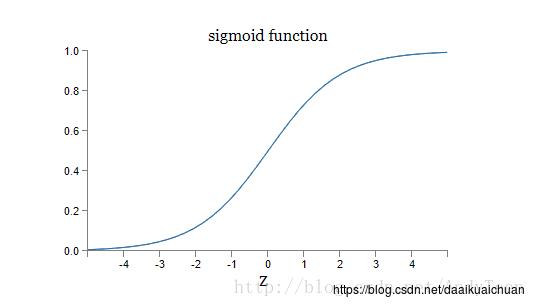
（1）sigmoid激活函数

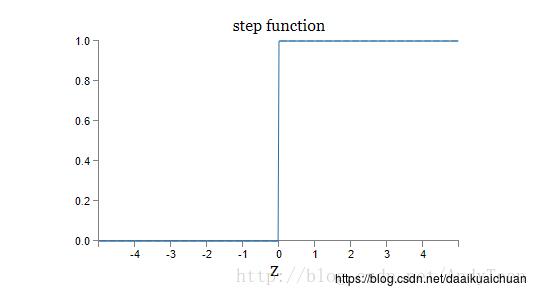
  神经元和感知器本质上是一样的，只不过我们说感知器的时候，它的激活函数是阶跃函数；而当我们说神经元时，激活函数往往选择为sigmoid函数或tanh函数。如下图所示：

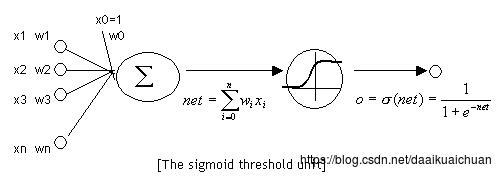
计算一个神经元的输出的方法和计算一个感知器的输出是一样的。假设神经元的输入是向量x⃗ x→，权重向量是w⃗ w→(偏置项是w0w0)，激活函数是sigmoid函数，则其输出yy：

 

 

y=sigmoid(w⃗ T⋅x⃗ )y=sigmoid(w→T⋅x→)

 

sigmoid函数的定义如下：

 

 

sigmoid(x)=11+e−xsigmoid(x)=11+e−x

 

将其带入前面的式子，得到：

 

 

y=11+e−w⃗ T⋅x⃗ y=11+e−w→T⋅x→

 

（2）sigmoid激活函数的优点

  sigmoid函数的导数是：

 

 

令y=sigmoid(x)则y′=y(1−y)令y=sigmoid(x)则y′=y(1−y)

 

  可以看到，sigmoid函数的导数可以用自身来表示。这样，一旦计算出sigmoid函数的值，计算它的导数的值就非常方便。而阶跃函数却不可导。在后面使用反向传播算法时，sigmoid函数便于求导，可以使用梯度下降法求极值，非常方便。

（3）常用的激活函数

1）Sigmoid ：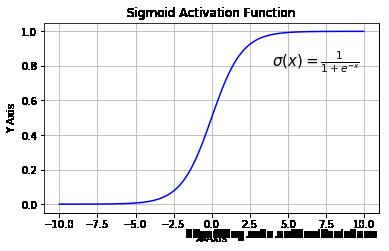

Sigmoid 函数的主要缺陷：

1. 梯度消失： 注意：Sigmoid 函数趋近 0 和 1 的时候变化率会变得平坦，也就是说，Sigmoid 的梯度趋近于 0。神经网络使用 Sigmoid 激活函数进行反向传播时，输出接近 0 或 1 的神经元其梯度趋近于 0。这些神经元叫作饱和神经元。因此，这些神经元的权重不会更新。此外，与此类神经元相连的神经元的权重也更新得很慢。该问题叫作梯度消失。因此，想象一下，如果一个大型神经网络包含 Sigmoid 神经元，而其中很多个都处于饱和状态，那么该网络无法执行反向传播；

2. 不以零为中心： Sigmoid 输出不以零为中心的；

3. 计算成本高昂： exp() 函数与其他非线性激活函数相比，计算成本高昂。下一个要讨论的非线性激活函数解决了 Sigmoid 函数中值域期望不为 0 的问题。

2）Tanh：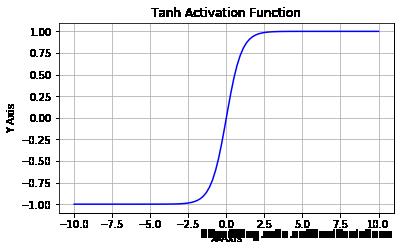

Tanh 函数的主要缺陷：

1. Tanh 函数也会有梯度消失的问题，因此在饱和时也会「杀死」梯度。

3）修正线性单元（ReLU）：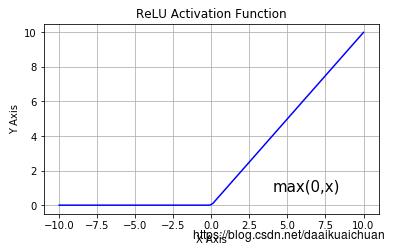

ReLU的主要缺陷：

1. 不以零为中心：和 Sigmoid 激活函数类似，ReLU 函数的输出不以零为中心；

2. 前向传导（forward pass）过程中，如果 x < 0，则神经元保持非激活状态，且在后向传导（backward pass）中「杀死」梯度。这样权重无法得到更新，网络无法学习。当 x = 0 时，该点的梯度未定义，但是这个问题在实现中得到了解决，通过采用左侧或右侧的梯度的方式。

3、神经网络的输出

  神经网络实际上就是一个输入向量x⃗ x→到输出向量y⃗ y→的函数，即：

 

 

y⃗ =fnetwork(x⃗ )y→=fnetwork(x→)

 

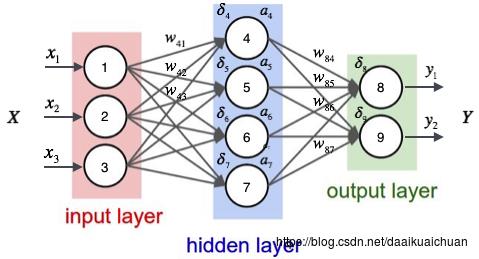
根据输入计算神经网络的输出，需要首先将输入向量x⃗ x→的每个元素xixi的值赋给神经网络的输入层的对应神经元，然后依次向前计算每一层的每个神经元的值，直到最后一层输出层的所有神经元的值计算完毕。最后，将输出层每个神经元的值串在一起就得到了输出向量y⃗ y→。接下来举一个例子来说明这个过程，我们先给神经网络的每个单元写上编号。

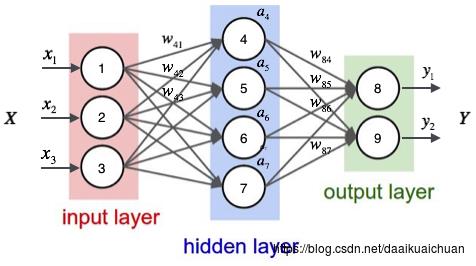
  神经网络的计算如果用矩阵来表示会很方便（当然逼格也更高），我们先来看看隐藏层的矩阵表示。

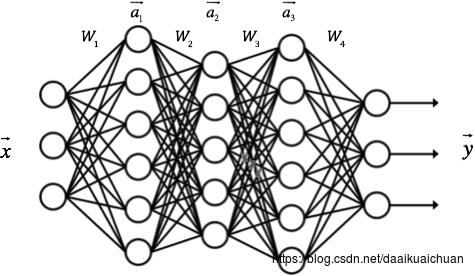
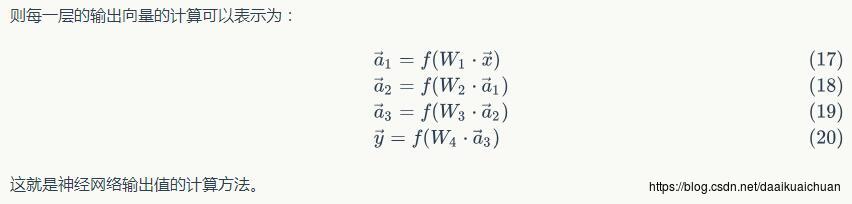
4、神经网络的训练

  现在，我们需要知道一个神经网络的每个连接上的权值是如何得到的。我们可以说神经网络是一个模型，那么这些权值就是模型的参数，也就是模型要学习的东西。然而，一个神经网络的连接方式、网络的层数、每层的节点数这些参数，则不是学习出来的，而是人为事先设置的。对于这些人为设置的参数，我们称之为超参数(Hyper-Parameters)。接下来，我们将要介绍神经网络的训练算法：反向传播算法。

（1）反向传播算法(Back Propagation)

  我们首先直观的介绍反向传播算法，最后再来介绍这个算法的推导。当然读者也可以完全跳过推导部分，因为即使不知道如何推导，也不影响你写出来一个神经网络的训练代码。事实上，现在神经网络成熟的开源实现多如牛毛，除了练手之外，你可能都没有机会需要去写一个神经网络。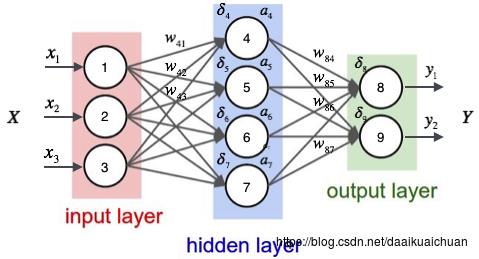

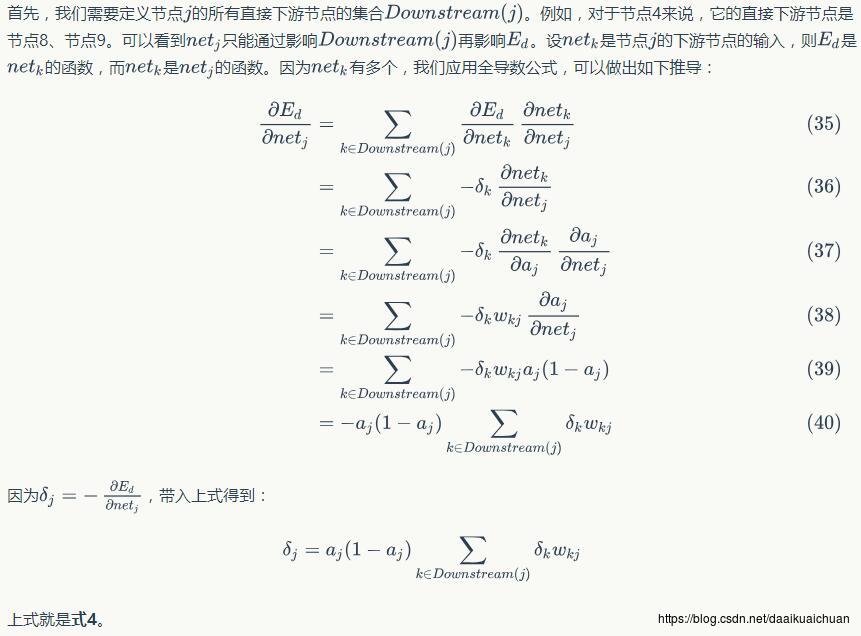
（2）反向传播算法的推导

  反向传播算法其实就是链式求导法则的应用。按照机器学习的通用套路，我们先确定神经网络的目标函数，然后用随机梯度下降优化算法去求目标函数最小值时的参数值。

我们取网络所有输出层节点的误差平方和作为目标函数：

 

 

Ed≡12∑i∈outputs(ti−yi)2Ed≡12∑i∈outputs(ti−yi)2

使用随机梯度下降算法对目标函数进行优化：

 

wji←wji−η∂Ed∂wjiwji←wji−η∂Ed∂wji

 

三、BP神经网络的流程

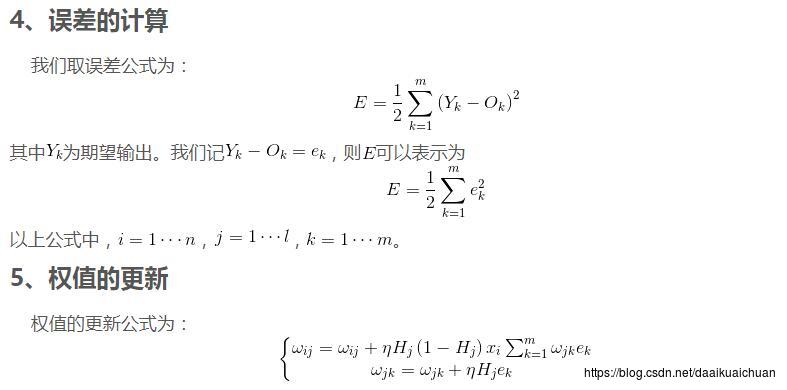
四、BP神经网络的总结

1、神经网络的主要概念

1. 单元/神经元；

2. 连接/权重/参数；

3. 偏置项；

4. 激活函数；

5. 输入层、隐藏层、输出层；

6. 反向传播。

2、BP神经网络重要参数

1. 学习率：首先，我们选择在训练数据上的代价立即开始下降而非震荡或者增加时的作为 η 阈值的估计，不需要太过精确，确定量级即可。如果代价在训练的前面若干回合开始下降，你就可以逐步增加 η 的量级，直到你找到一个的值使得在开始若干回合代价就开始震荡或者增加；相反，如果代价函数曲线开始震荡或者增加，那就尝试减小量级直到你找到代价在开始回合就下降的设定，取阈值的一半就确定了学习速率 。在这里使用训练数据的原因是学习速率主要的目的是控制梯度下降的步长，监控训练代价是最好的检测步长过大的方法；

2. 迭代次数：我们需要再明确一下什么叫做分类准确率不再提升，这样方可实现提前停止。正如我们已经看到的，分类准确率在整体趋势下降的时候仍旧会抖动或者震荡。如果我们在准确度刚开始下降的时候就停止，那么肯定会错过更好的选择。一种不错的解决方案是如果分类准确率在一段时间内不再提升的时候终止。建议在更加深入地理解 网络训练的方式时，仅仅在初始阶段使用 10 回合不提升规则，然后逐步地选择更久的回合，比如 20 回合不提升就终止，30回合不提升就终止，以此类推；

3. 隐藏层的选取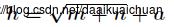：其中h为隐含层节点数目，m为输入层节点数目，n为输出层节点数目，a为1~10之间的调节常数。

3、关于BP神经网络的几点思考

1. 反向传播算法传播的是什么：传播的是误差项；

2. 隐藏层的作用：多层神经网络，可以认为将原始输入数据，在每一层隐含层上做了多个二分类，二分类的个数即为该隐含层的神经元个数。多个隐藏层就是为了让线性不可分的数据变得线性可分；

3. 神经网络和感知器的区别：神经网络的隐层神经元使用的是连续的Sigmoid非线性函数，而感知器使用阶梯函数这一非线性函数。这意味着神经网络函数对网络参数来说是可微的，这一性质在神经网络训练过程中起这重要的作用；

4. 隐藏层的激活函数不可以取线性函数的原因：如果所有隐藏层神经元的激活函数都取线性函数的话，那么我们将总能找到一个没有隐藏层的网络与之等价。这是因为，多个线性变换的组合，也是一个线性变换（多个线性变换的组合可以用一个线性变换代替）。此时，如果隐藏层神经元的数量少于输入或输出神经元的数量，那么这个网络所产生的变换就不是一般意义上的从输入到输出的线性变换，这是因为隐含单元出现的维度降低造成了信息丢失；

5. 实际应用中的神经网络结构：输入层单元数 = 特征的维度；输出层单元数 = 类别个数；隐层单元数理论上是越多越好，但是单元数越多意味着计算量越大，故其取值一般稍大于传入特征数或者几倍关系也可以。基于隐藏层的数目，一般默认使用1个隐层的神经网络，也可以使用多个隐层的神经网络，若为多层神经网路一般默认所有隐层具有相同的单元数 ；

6. 神经网络中的参数更新：一般使用随机梯度下降法（SGD），而非批量梯度下降，原因是：1. SGD可以更加高效的处理数据中的冗余性（假设我们将数据集中所有样本都复制一次，这样包含了一半的冗余信息，使用PGD的计算量也会增大一倍，而SGD不受影响）；2. 有机会跳出局部最小值到达全局最小值（因为整个数据集的关于误差函数的驻点通常不会是每个数据点各自的驻点）。

%% Machine Learning Online --Neural Network Learning
 
%  Instructions
%  ------------
% 
%  This file contains code that helps you get started on the
%  linear exercise. You will need to complete the following functions 
%  in this exericse:
%
%     sigmoidGradient.m
%     randInitializeWeights.m
%     nnCostFunction.m
%
%  For this exercise, you will not need to change any code in this file,
%  or any other files other than those mentioned above.
%
 
%% Initialization
clear ; close all; clc
 
%% Setup the parameters you will use for this exercise
input_layer_size  = 400;  % 20x20 Input Images of Digits
hidden_layer_size = 25;   % 25 hidden units
num_labels = 10;          % 10 labels, from 1 to 10   
                          % (note that we have mapped "0" to label 10)
 
%% =========== Part 1: Loading and Visualizing Data =============
%  We start the exercise by first loading and visualizing the dataset. 
%  You will be working with a dataset that contains handwritten digits.
%
 
% Load Training Data
fprintf('Loading and Visualizing Data ...\\n')
 
load('ex4data1.mat');
m = size(X, 1);
 
% Randomly select 100 data points to display
sel = randperm(size(X, 1));
sel = sel(1:100);
 
displayData(X(sel, :));
 
fprintf('Program paused. Press enter to continue.\\n');
pause;
 
 
%% ================ Part 2: Loading Parameters ================
% In this part of the exercise, we load some pre-initialized 
% neural network parameters.
 
fprintf('\\nLoading Saved Neural Network Parameters ...\\n')
 
% Load the weights into variables Theta1 and Theta2
load('ex4weights.mat');
 
% Unroll parameters 
nn_params = [Theta1(:) ; Theta2(:)];
 
%% ================ Part 3: Compute Cost (Feedforward) ================
%  To the neural network, you should first start by implementing the
%  feedforward part of the neural network that returns the cost only. You
%  should complete the code in nnCostFunction.m to return cost. After
%  implementing the feedforward to compute the cost, you can verify that
%  your implementation is correct by verifying that you get the same cost
%  as us for the fixed debugging parameters.
%
%  We suggest implementing the feedforward cost *without* regularization
%  first so that it will be easier for you to debug. Later, in part 4, you
%  will get to implement the regularized cost.
%
fprintf('\\nFeedforward Using Neural Network ...\\n')
 
% Weight regularization parameter (we set this to 0 here).
lambda = 0;
 
J = nnCostFunction(nn_params, input_layer_size, hidden_layer_size, ...
                   num_labels, X, y, lambda);
 
fprintf(['Cost at parameters (loaded from ex4weights): %f '...
         '\\n(this value should be about 0.287629)\\n'], J);
 
fprintf('\\nProgram paused. Press enter to continue.\\n');
pause;
 
%% =============== Part 4: Implement Regularization ===============
%  Once your cost function implementation is correct, you should now
%  continue to implement the regularization with the cost.
%
 
fprintf('\\nChecking Cost Function (w/ Regularization) ... \\n')
 
% Weight regularization parameter (we set this to 1 here).
lambda = 1;
 
J = nnCostFunction(nn_params, input_layer_size, hidden_layer_size, ...
                   num_labels, X, y, lambda);
 
fprintf(['Cost at parameters (loaded from ex4weights): %f '...
         '\\n(this value should be about 0.383770)\\n'], J);
 
fprintf('Program paused. Press enter to continue.\\n');
pause;
 
 
%% ================ Part 5: Sigmoid Gradient  ================
%  Before you start implementing the neural network, you will first
%  implement the gradient for the sigmoid function. You should complete the
%  code in the sigmoidGradient.m file.
%
 
fprintf('\\nEvaluating sigmoid gradient...\\n')
 
g = sigmoidGradient([-1 -0.5 0 0.5 1]);
fprintf('Sigmoid gradient evaluated at [-1 -0.5 0 0.5 1]:\\n  ');
fprintf('%f ', g);
fprintf('\\n\\n');
 
fprintf('Program paused. Press enter to continue.\\n');
pause;
 
 
%% ================ Part 6: Initializing Pameters ================
%  In this part of the exercise, you will be starting to implment a two
%  layer neural network that classifies digits. You will start by
%  implementing a function to initialize the weights of the neural network
%  (randInitializeWeights.m)
 
fprintf('\\nInitializing Neural Network Parameters ...\\n')
 
initial_Theta1 = randInitializeWeights(input_layer_size, hidden_layer_size);
initial_Theta2 = randInitializeWeights(hidden_layer_size, num_labels);
 
% Unroll parameters
initial_nn_params = [initial_Theta1(:) ; initial_Theta2(:)];
 
 
%% =============== Part 7: Implement Backpropagation ===============
%  Once your cost matches up with ours, you should proceed to implement the
%  backpropagation algorithm for the neural network. You should add to the
%  code you've written in nnCostFunction.m to return the partial
%  derivatives of the parameters.
%
fprintf('\\nChecking Backpropagation... \\n');
 
%  Check gradients by running checkNNGradients
checkNNGradients;
 
fprintf('\\nProgram paused. Press enter to continue.\\n');
pause;
 
 
%% =============== Part 8: Implement Regularization ===============
%  Once your backpropagation implementation is correct, you should now
%  continue to implement the regularization with the cost and gradient.
%
 
fprintf('\\nChecking Backpropagation (w/ Regularization) ... \\n')
 
%  Check gradients by running checkNNGradients
lambda = 3;
checkNNGradients(lambda);
 
% Also output the costFunction debugging values
debug_J  = nnCostFunction(nn_params, input_layer_size, ...
                          hidden_layer_size, num_labels, X, y, lambda);
 
fprintf(['\\n\\nCost at (fixed) debugging parameters (w/ lambda = %f): %f ' ...
         '\\n(for lambda = 3, this value should be about 0.576051)\\n\\n'], lambda, debug_J);
 
fprintf('Program paused. Press enter to continue.\\n');
pause;
 
 
%% =================== Part 8: Training NN ===================
%  You have now implemented all the code necessary to train a neural 
%  network. To train your neural network, we will now use "fmincg", which
%  is a function which works similarly to "fminunc". Recall that these
%  advanced optimizers are able to train our cost functions efficiently as
%  long as we provide them with the gradient computations.
%
fprintf('\\nTraining Neural Network... \\n')
 
%  After you have completed the assignment, change the MaxIter to a larger
%  value to see how more training helps.
options = optimset('MaxIter', 50);
 
%  You should also try different values of lambda
lambda = 1;
 
% Create "short hand" for the cost function to be minimized
costFunction = @(p) nnCostFunction(p, ...
                                   input_layer_size, ...
                                   hidden_layer_size, ...
                                   num_labels, X, y, lambda);
 
% Now, costFunction is a function that takes in only one argument (the
% neural network parameters)
[nn_params, cost] = fmincg(costFunction, initial_nn_params, options);
 
% Obtain Theta1 and Theta2 back from nn_params
Theta1 = reshape(nn_params(1:hidden_layer_size * (input_layer_size + 1)), ...
                 hidden_layer_size, (input_layer_size + 1));
 
Theta2 = reshape(nn_params((1 + (hidden_layer_size * (input_layer_size + 1))):end), ...
                 num_labels, (hidden_layer_size + 1));
 
fprintf('Program paused. Press enter to continue.\\n');
pause;
 
 
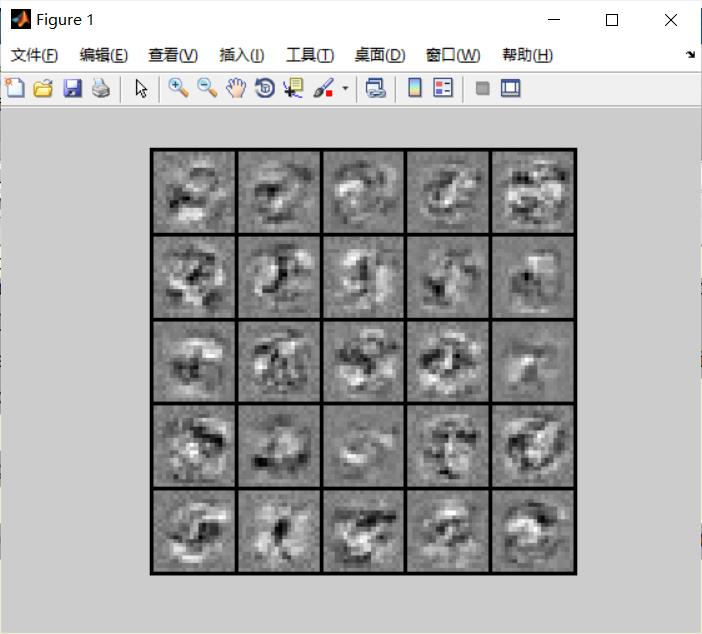
%% ================= Part 9: Visualize Weights =================
%  You can now "visualize" what the neural network is learning by 
%  displaying the hidden units to see what features they are capturing in 
%  the data.
 
fprintf('\\nVisualizing Neural Network... \\n')
 
displayData(Theta1(:, 2:end));
 
fprintf('\\nProgram paused. Press enter to continue.\\n');
pause;
 
%% ================= Part 10: Implement Predict =================
%  After training the neural network, we would like to use it to predict
%  the labels. You will now implement the "predict" function to use the
%  neural network to predict the labels of the training set. This lets
%  you compute the training set accuracy.
 
pred = predict(Theta1, Theta2, X);
 
fprintf('\\nTraining Set Accuracy: %f\\n', mean(double(pred == y)) * 100);