lsp预测基于粒子群优化强化学习预测matlab源码
Posted Matlab走起
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了lsp预测基于粒子群优化强化学习预测matlab源码相关的知识,希望对你有一定的参考价值。
一、强化学习概述
1.强化学习简介
(1)强化学习是机器学习中的一个领域,强调如何基于环境而行动,以取得最大化的预期利益。其灵感来源于心理学中的行为主义理论,即有机体如何在环境给予的奖励或惩罚的刺激下,逐步形成对刺激的预期,产生能获得最大利益的习惯性行为。
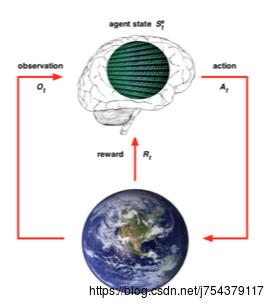
(2)强化学习最早可以追溯到巴甫洛夫的条件反射实验,它从动物行为研究和优化控制两个领域独立发展,最终经Bellman之手将其抽象为马尔可夫决策过程 (Markov Decision Process,MDP)
![]()
2.发展历程:
1956年Bellman提出了动态规划方法。
1977年Werbos提出只适应动态规划算法。
1988年sutton提出时间差分算法。
1992年Watkins 提出Q-learning 算法。
1994年rummery 提出Saras算法。
1996年Bersekas提出解决随机过程中优化控制的神经动态规划方法。
2006年Kocsis提出了置信上限树算法。
2009年kewis提出反馈控制只适应动态规划算法。
2014年silver提出确定性策略梯度(Policy Gradients)算法。
2015年Google-deepmind 提出Deep-Q-Network算法。
可见,强化学习已经发展了几十年,并不是一门新的技术。在2016年,AlphaGo击败李世石之后,融合了深度学习的强化学习技术大放异彩,成为这两年最火的技术之一。总结来说,强化学习就是一个古老而又时尚的技术。
3.MDP(马儿可夫决策过程)
![]()
S: 表示状态集(states),有s∈S,si表示第i步的状态。
A:表示一组动作(actions),有a∈A,ai表示第i步的动作。
?sa: 表示状态转移概率。?s? 表示的是在当前s ∈ S状态下,经过a ∈ A作用后,会转移到的其他状态的概率分布情况。比如,在状态s下执行动作a,转移到s'的概率可以表示为p(s'|s,a)。
R: S×A⟼ℝ ,R是回报函数(reward function)。有些回报函数状态S的函数,可以简化为R: S⟼ℝ。如果一组(s,a)转移到了下个状态s',那么回报函数可记为r(s'|s, a)。如果(s,a)对应的下个状态s'是唯一的,那么回报函数也可以记为r(s,a)。
γ:折现因子
4.why RL?
强化学习所解决的问题的特点:
- 智能体和环境之间不断进行交互
- 搜索和试错
- 延迟奖励(当前所做的动作可能很多步之后才会产生相应的结果)
目标:
- 获取更多的累积奖励
- 获得更可靠的估计
强化学习 (Reinforcement Learning) 是一个机器学习大家族中的分支, 由于近些年来的技术突破, 和深度学习 (Deep Learning) 的整合, 使得强化学习有了进一步的运用。比如让计算机学着玩游戏, AlphaGo 挑战世界围棋高手, 都是强化学习在行的事。强化学习也是让你的程序从对当前环境完全陌生, 成长为一个在环境中游刃有余的高手。
5.总结:
深度强化学习全称是 Deep Reinforcement Learning(DRL),其所带来的推理能力 是智能的一个关键特征衡量,真正的让机器有了自我学习、自我思考的能力。
深度强化学习(Deep Reinforcement Learning,DRL)本质上属于采用神经网络作为值函数估计器的一类方法,其主要优势在于它能够利用深度神经网络对状态特征进行自动抽取,避免了人工 定义状态特征带来的不准确性,使得Agent能够在更原始的状态上进行学习。
二、强化学习求解方法
1.动态规划方法
基石:贝尔曼方程
(1)贝尔曼方程:
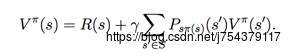
![]()
贝尔曼最优方程:
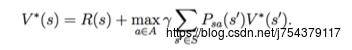
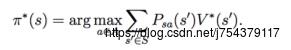
如何求解贝尔曼方程呢?
本质上就是个线性规划问题,多个方程,多个未知数,进行求解,如下,假设每一步的即使奖励是-0.2,有三个未知状态V(0,1),V(1,1),V(1,0),损失因子是1,则在如下的策略下,得到的贝尔曼方程如下:
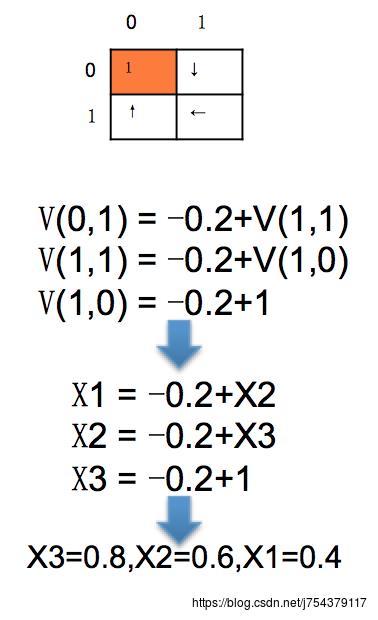
但是当未知变量不断增大,线性规划则很难求解,这时需要使用动态规划进行不断迭代,让其状态值收敛。
(2)值迭代
In Value Iteration, you start with a randon value function and then find a new (improved) value function in a iterative process, until reaching the optimal value function. Notice that you can derive easily the optimal policy from the optimal value function. This process is based on the Optimality Bellman operator.
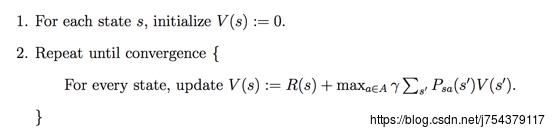
(3)策略迭代
In Policy Iteration algorithms, you start with a random policy, then find the value function of that policy (policy evaluation step), then find an new (improved) policy based on the previous value function, and so on. In this process, each policy is guaranteed to be a strict improvement over the previous one (unless it is already optimal). Given a policy, its value function can be obtained using the Bellman operator.

(4)算法详细对比:


- 根据策略迭代算法,每一次迭代都要进行策略评估和策略提升,直到二者都收敛。可我们的目标是选出最优的策略,那么有没有可能在策略评估值没有收敛的情况下,最优策略已经收敛了呢?答案是有这个可能
- 策略迭代的收敛速度更快一些,在状态空间较小时,最好选用策略迭代方法。当状态空间较大时,值迭代的计算量更小一些
(5)GridWorld举例(分别用策略迭代和值迭代进行求解)

策略迭代过程:
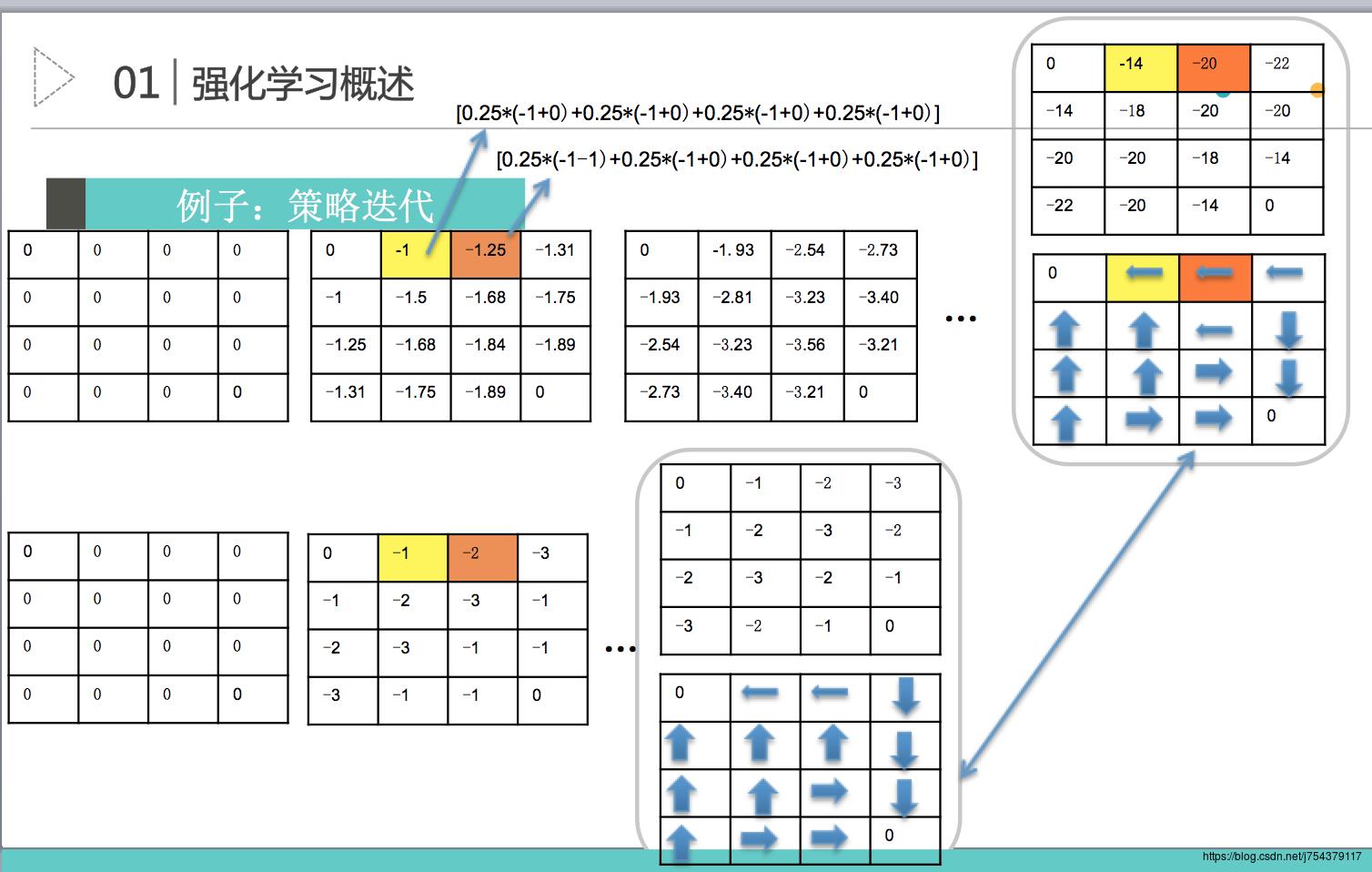
值迭代过程:
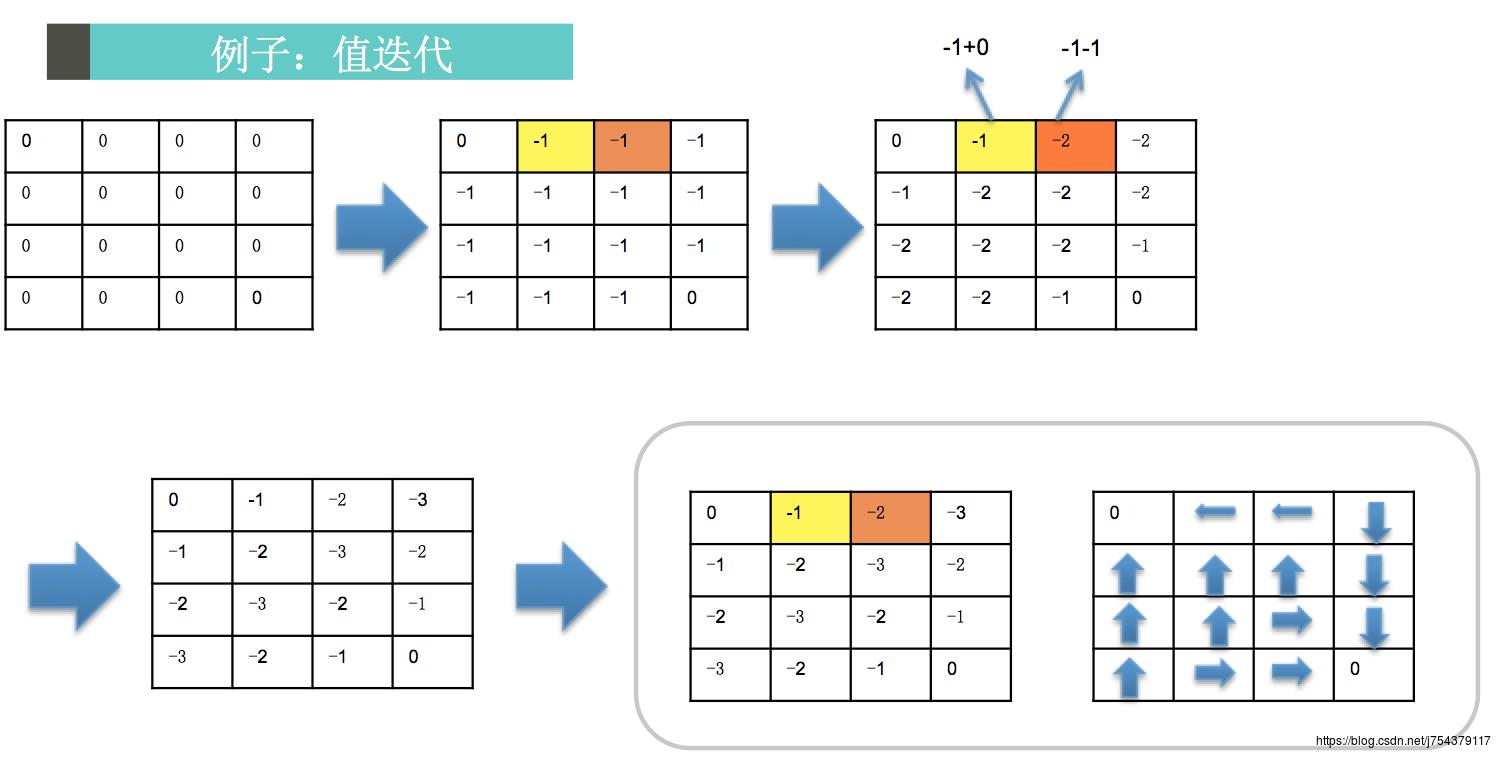
2.蒙特卡洛方法
上面的动态规划方法,是一种较为理想的状态,即所有的参数都提前知道,比如状态转移概率,及奖励等等。然而显示情况是未知的,这时候有一种手段是采用蒙特卡洛采样,基于大数定律,基于统计计算出转移概率值;比如当你抛硬币的次数足够多,那么正面和反面的概率将会越来越接近真实情况。
3.时间差分方法
基于动态规划和蒙特卡洛
三、强化学习算法分类
1.分类一:
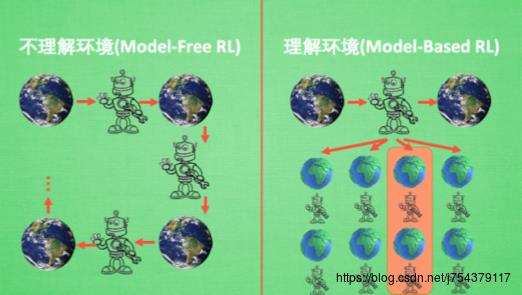
基于理不理解所处环境来进行分类:
Model-free:环境给了我们什么就是什么. 我们就把这种方法叫做 model-free, 这里的 model 就是用模型来表示环境
Model-based:那理解了环境也就是学会了用一个模型来代表环境, 所以这种就是 model-based 方法
2.分类二:
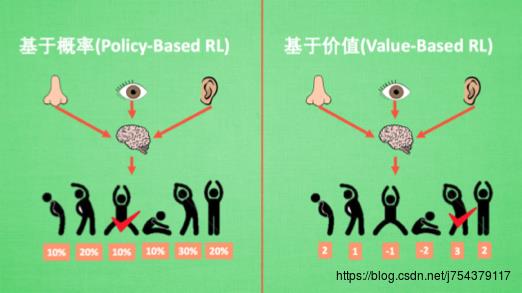
一类是直接输出各个动作概率,另一个是输出每个动作的价值;前者适用于连续动作情况,后者无法表示连续动作的价值。
3.分类三:
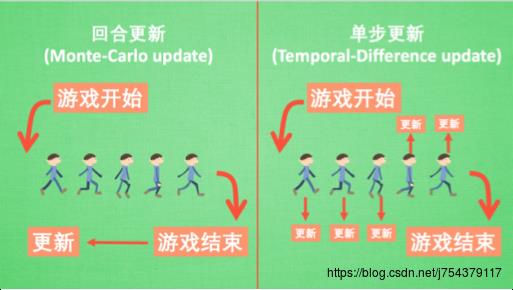
4.分类四:
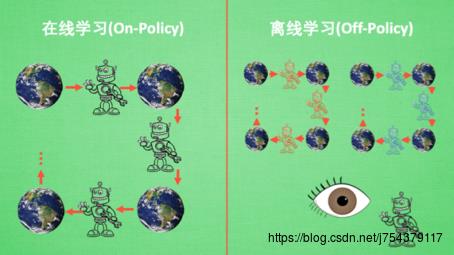
判断on-policy和off-policy的关键在于,你所估计的policy或者value-function和你生成样本时所采用的policy是不是一样。如果一样,那就是on-policy的,否则是off-policy的。
总结各常用算法的分类:
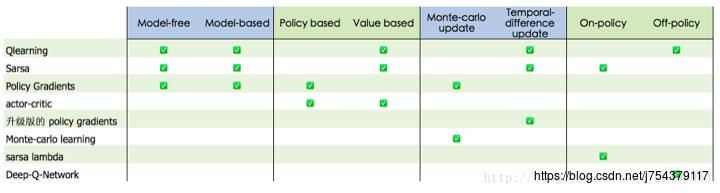
四、代表性算法
1.Q-learning
(1)四个基本组成成分:
- Q表:Q(s,a),状态s下执行动作a的累积价值
- 定义动作:选择动作
- 环境反馈:做出行为后,环境的反馈
- 环境更新
(2)算法公式:

(3)算法决策:

(4)算法更新:
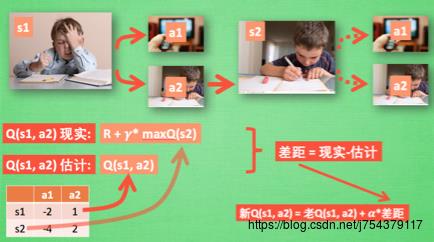
(5)代码实现框架:
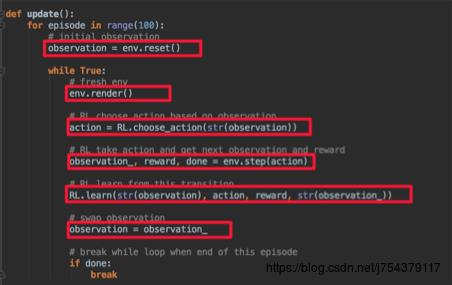
2.Sarsa:
与Q-learning基本类似,唯一的区别是更新方式不一样
(1)算法公式:

(2)与Q-learning的区别:Sarsa是on-policy的,Q-learning是off-policy的

(3)更新过程:
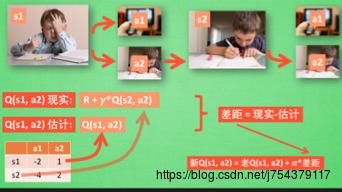
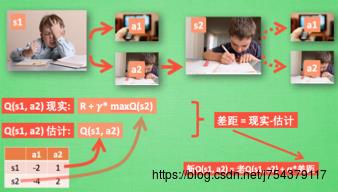
前者是Sarsa,后者是Q-learning
(4)代码中展现不同:
Sarsa:
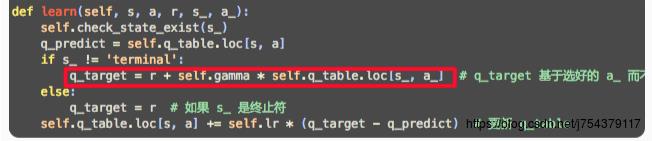
Q-learning:
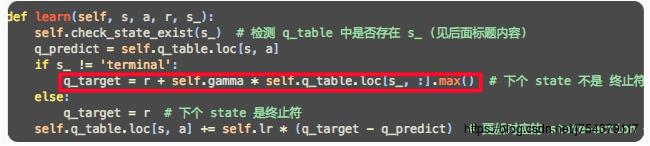
(5)代码实现框架:
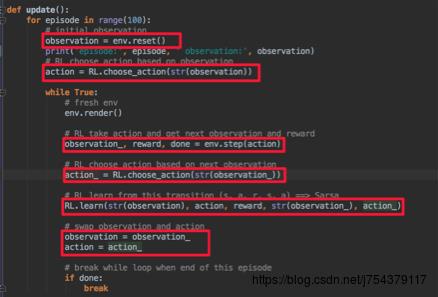
3.大名鼎鼎的DQN
Deepmind就是因为DQN这篇论文,被谷歌收购
(1)由来:
-
DQN(Deep Q Network)是一种融合了神经网络和Q learning的方法.
-
有些问题太复杂,Q表无法存储,即使可以存储,搜索也很麻烦。故而,将Q表用神经网络进行替代。
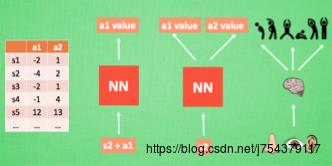
(2)增加了两个新特性:
Experience replay:每次DQN更新的时候,随机抽取一些之前的经历进行学习。随机抽取这种打乱了经历之间的相关性,使得神经网络更新更有效率。
Fixed Q-targets:使用两个结构相同但参数不同的神经网络,预测Q估计的神经网络具备最新的参数,而预测Q现实的神经网络使用的参数则是很久以前的。
(3)算法公式:

paper地址:Playing Atari with Deep Reinforcement Learning
(4)DQN代码实现框架:
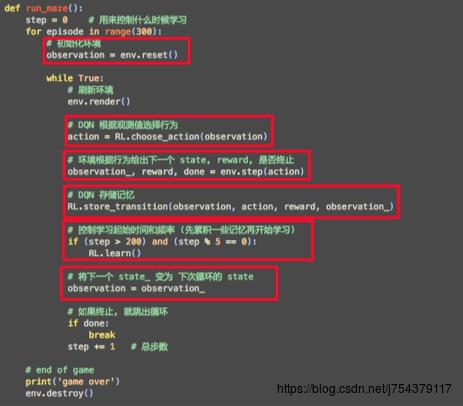
可以看到基本上Q-learning一模一样,只是有一处不一样,就是多了存储记忆,并且批量进行学习。
clear;
warning off all;
format compact;
load shujv.mat;
train_y=(train_y-1)*2+1;
test_y=(test_y-1)*2+1;
assert(isfloat(train_x), 'train_x must be a float');
assert(all(train_x(:)>=0) && all(train_x(:)<=1), 'all data in train_x must be in [0:1]');
assert(isfloat(test_x), 'test_x must be a float');
assert(all(test_x(:)>=0) && all(test_x(:)<=1), 'all data in test_x must be in [0:1]');
%%%%%%%%%%%%%%%%%%%%This is the model of broad learning system for%%%%%% 这是用于 m2+m3 增强节点和 m1 特征节点的增量的宽度学习系统模型
%%%%%%%%%%%%%%%%%%%%increment of m2+m3 enhancement nodes and m1 feature nodes %%%%%%%%%%%%%%%%%%%%%%%%
C = 2^-30;
s = 0.7 ; %the l2 regularization parameter and the shrinkage scale of the enhancement nodes l2正则化参数和增强节点的缩小比例
N11=20; %feature nodes per window 每个窗口的特征映射节点数
N2=30; % number of windows of feature nodes 特征节点的窗口数
N33=550; % number of enhancement nodes 增强节点数
epochs=1;% number of epochs epochs的周期数
m1=20;%number of feature nodes per increment step 每个增量步长中特征节点数
m2=80;%number of enhancement nodes related to the incremental feature nodes per increment step 每个增量步长中,与增量特征节点相关的增强节点的数量
m3=200;%number of enhancement nodes in each incremental learning 每次增量学习中增强节点的数量
l=1;% steps of incremental learning 增量学习的步长
train_err_t=zeros(epochs,l);test_err_t=zeros(epochs,l);train_time_t=zeros(epochs,l);test_time_t=zeros(epochs,l);
Testing_time_t=zeros(epochs,1);Training_time_t=zeros(epochs,1);
% rand('state',67797325) % 12000 %%%%% The random seed recommended by the
% reference HELM [10]. 参考HELM [10]生成的随机数
N1=N11; N3=N33;
for i=1:epochs
[train_err,test_err,train_time,test_time,Testing_time,Training_time] = bls_train_enhancefeature(train_x,train_y,test_x,test_y,s,C,N1,N2,N3,m1,m2,m3,l);
train_err_t(i,:)=train_err;test_err_t(i,:)=test_err;train_time_t(i,:)=train_time;test_time_t(i,:)=test_time;
Testing_time_t(i)=Testing_time;Training_time_t(i)=Training_time;
end
save ( [ 'cwt_result_enhancefeature'], 'train_err_t', 'test_err_t', 'train_time_t', 'test_time_t','Testing_time_t','Training_time_t');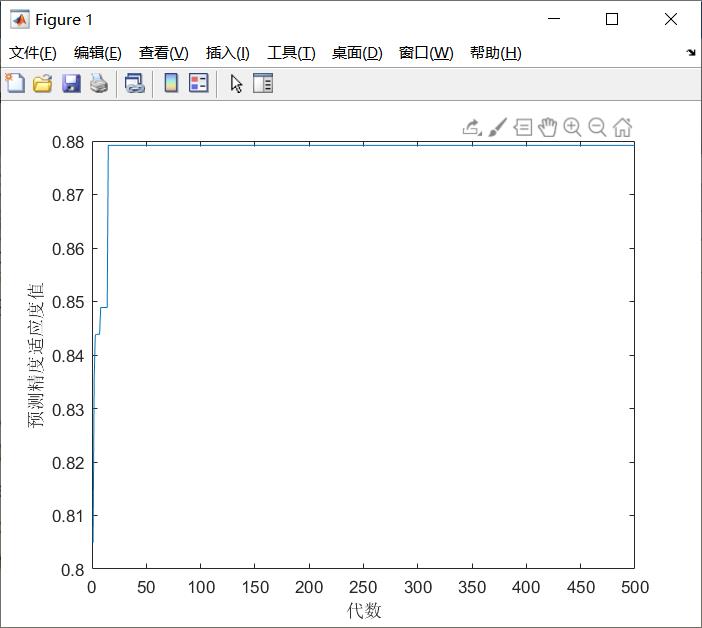
以上是关于lsp预测基于粒子群优化强化学习预测matlab源码的主要内容,如果未能解决你的问题,请参考以下文章
优化预测基于matlab混沌粒子群算法优化极限学习机ELM预测含Matlab源码 1586期
ELM数据预测基于matlab粒子群算法优化ELM数据预测(含前后对比)含Matlab源码 449期