路径规划基于改进差分算法实现三维多无人机协同航迹规划
Posted Matlab走起
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了路径规划基于改进差分算法实现三维多无人机协同航迹规划相关的知识,希望对你有一定的参考价值。
一、差分进化算法的介绍
差分进化算法(Differential Evolution, DE)是一种基于群体差异的启发式随机搜索算法,该算法是由R.Storn和K.Price为求解Chebyshev多项式而提出的。DE算法也属于智能优化算法,与前面的启发式算法,如ABC,PSO等类似,都属于启发式的优化算法。DE算法是我在一篇求解盒子覆盖问题论文中使用的一种优化算法。
二、差分进化算法的流程
- 初始化种群
- 变异
- 交叉
- 选择
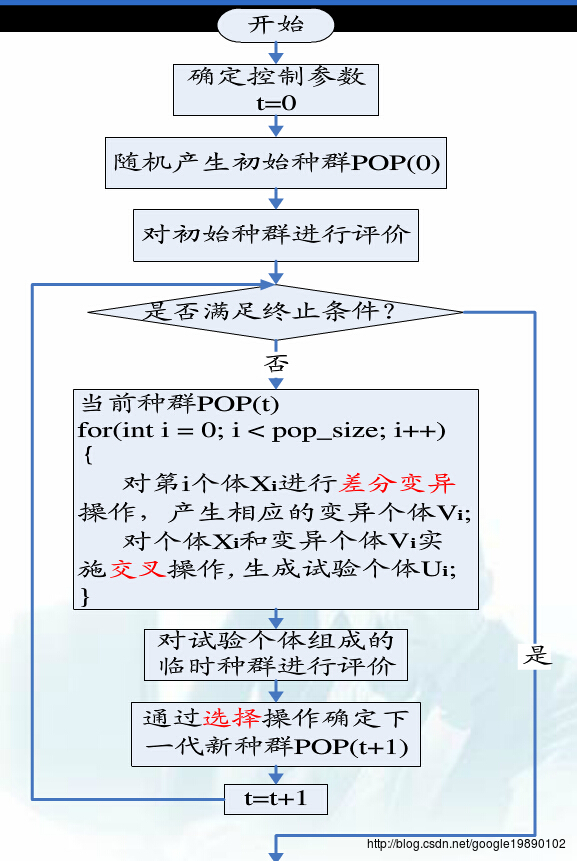
(DE流程)
三、差分进化的具体步骤
对于无约束优化问题

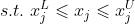
利用差分进化求解这样的优化问题,主要分为初始化、变异、交叉和选择等几项操作。
1、初始化
如前面的的群智能优化算法一样,差分进化也需要初始化种群:
其中, 是第
是第 个个体,
个个体,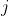 表示第
表示第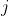 维。
维。
其中,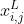 和
和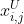 分别为第
分别为第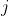 维的下界和上界,
维的下界和上界,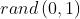 表示在区间
表示在区间 上的随机数。
上的随机数。
2、变异
DE算法通过差分策略实现个体变异,常见的差分策略是随机选取种群中两个不同的个体,将其向量差缩放后与待变异个体进行向量合成。
其中,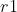 ,
,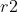 和
和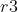 是三个随机数,区间为
是三个随机数,区间为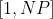 ,
, 称为缩放因子,为一个确定的常数。
称为缩放因子,为一个确定的常数。 表示第
表示第 代。
代。
3、交叉
交叉操作的目的是随机选择个体,因为差分进化也是一种随机算法,交叉操作的方法是:
其中,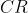 称为交叉概率。通过概率的方式随机生成新的个体。
称为交叉概率。通过概率的方式随机生成新的个体。
4、选择
在DE中采用的是贪婪选择的策略,即选择较优的个体作为新的个体。
%清空环境
clear;
%定义地形对象
cTerrain = CTerrain3D;
%定义威胁区对象
cTread = CTread;
%调整为统一的图形环境
figure('Renderer','opengl');
%绘制地形和威胁区
cTerrain.draw();
cTread.draw();
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%数据形式说明
%xs 初始点位置集合,三维点集
%yt 目标点位置集合,三维点集
%MxsEna 能力矩阵,集合中的二元组表示最大最小飞行速度
%MxsDIs 最大航程矩阵,集合中的值表示UAV最大可飞的距离
%MytTOrd 任务点间的时序坐标,要求尽量在前面的先执行
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%调用目标分配算法
%AssignType表示不同的模型,1, N=M; 2, N>M; 3, N<M
%Key表示算法执行次数, 0,执行一次,1,执行多次
AssignType =1;
Key = 0;
%时间测试
Time = cputime;
%% 第一种情况的实验
if AssignType == 1
%%%%%%%%%%%%%%%%%%%%%%%数据区%%%%%%%%%%%%
xs = [%11 2 3;2 17 5; 34 26 7;5 2 2;6 33 3;27 34 6;21 45 5;25 12 3;22 17 11;13 31 12;
%45 21 11; 36 22 11;13 21 16;41 25 10;25 25 11;53 12 14;22 12 12;18 32 11; 67 34 12;26 16 15;
78 20 15;93 31 12;31 20 13;112 32 15; 134 26 17;45 52 12;36 63 13;67 34 16;21 85 15;32 62 13;];
yt = [%40 210 12;170 90 13 ; 80 197 21 ;172 120 13;160 56 13;160 143 21;170 200 21;113 200 12;97 134 16;100 145 11;
%81 101 21; 72 152 12; 133 60 11;84 164 21; 150 90 21;146 121 12; 167 54 12; 108 165 12;99 120 21;110 143 11;
70 181 12;15 133 13 ; 19 151 12 ;160 192 13;101 120 23;160 113 12;82 101 11;173 140 12;182 65 14; 128 156 12;];
MxsEna=[%0.2 0.3; 0.2 0.4;0.4 0.75;0.3 0.6;0.2 0.3;0.35 0.45;0.3 0.5;0.3 0.6;0.2 0.3; 0.2 0.4;
% 0.4 0.75;0.3 0.6;0.2 0.3;0.35 0.45;0.3 0.5;0.3 0.6;0.2 0.3;0.35 0.45;0.3 0.5;0.3 0.6;
0.2 0.3; 0.2 0.4;0.4 0.75;0.3 0.6;0.2 0.3;0.35 0.45;0.3 0.5;0.3 0.6;0.3 0.5;0.3 0.6;];
MxsDis=[%400 700 650 500 700 900 450 610 400 700
%650 500 700 900 450 610 700 900 450 610
500 700 300 350 700 900 450 610 450 610];
ytW = [%1 3 4 2 1 1 3 2 1 2
%3 2 1 3 2 1 2 3 2 1
1 1 1 1 1 1 1 1 1 1];
MytTOrd=[3 4; 5 2; 6 8; 7 4;];
%引入新的协同矩阵,最大起始时间矩阵
Twait = [];
Twindow=[];
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
if Key == 0
%%%%%%%%%%%%%%%%%%%%%%算法执行区%%%%%%%%%%%%%%%%%%
%调用目标分配算法,并取得解和相关数据,计算算法耗费时间
%定义目标分配算法对象
DDE1 = DMDEAssignTarget(cTerrain,xs,yt,MxsEna,MxsDis,ytW,MytTOrd,Twait,Twindow,1);
% MC = Cal1.GetMcost();
%Cal1 = CallocationTargetOld1(cTerrain);
%标签显示文字
xlabel('X/km')
ylabel('Y/km')
zlabel('Z/km')
%DDEAssign1=DDEAssignTarget1(cTerrain,xs,yt,MxsEna,MxsDis,ytW,MytTOrd);
%执行run并返回结果集
t1 = cputime;
[solU solT solC solF ] = DDE1.run();
Time = cputime -t1;
% %结果
solU
solT
solC
solF
Time
else if Key == 1
for i=1:10
DDE1 = DMDEAssignTarget(cTerrain,xs,yt,MxsEna,MxsDis,ytW,MytTOrd,Twait,Twindow,i);
% MC = Cal1.GetMcost();
%Cal1 = CallocationTargetOld1(cTerrain);
%标签显示文字
xlabel('X/km')
ylabel('Y/km')
zlabel('Z/km')
%DDEAssign1=DDEAssignTarget1(cTerrain,xs,yt,MxsEna,MxsDis,ytW,MytTOrd);
%执行run并返回结果集
t1 = cputime;
[solU solT solC solF ] = DDE1.run();
solu(i,:) = solU;
solt(i,:) = solT;
solc(i,:) = solC;
solf(i,:) = solF;
Time(i,:) = cputime -t1;
end %i
% %结果
solu
solt
solc
solf
Time
end % key=1
end % key=0
else if AssignType == 2
%% 第二种实验的情况
%%%%%%%%%%%%%%%%%%%%%%%数据区%%%%%%%%%%%%
xs = [%11 2 3;2 17 5; 34 26 7;5 2 2;6 33 3;27 34 6;21 45 5;25 12 3;22 17 11;13 31 12;
%45 21 11; 36 22 11;13 21 16;41 25 10;25 25 11;53 12 14;22 12 12;18 32 11; 67 34 12;26 16 15;
78 20 15;93 31 12;31 20 13;112 32 15; 134 26 17;45 52 12;36 63 13;67 34 16;21 85 15;32 62 13;];
yt = [%40 210 12;170 90 13 ; 80 197 21 ;172 120 13;160 56 13;160 143 21;170 200 21;113 200 12;97 134 16;100 145 11;
%81 101 21; 72 152 12; 133 60 11;84 164 21; 150 90 21;146 121 12; 167 54 12; 108 165 12;99 120 21;110 143 11;
70 181 12;15 133 13 ; 19 151 12 ;160 192 13 ];
MxsEna=[%0.2 0.3; 0.2 0.4;0.4 0.75;0.3 0.6;0.2 0.3;0.35 0.45;0.3 0.5;0.3 0.6;0.2 0.3; 0.2 0.4;
% 0.4 0.75;0.3 0.6;0.2 0.3;0.35 0.45;0.3 0.5;0.3 0.6;0.2 0.3;0.35 0.45;0.3 0.5;0.3 0.6;
0.2 0.3; 0.2 0.4;0.4 0.75;0.3 0.6;0.2 0.3;0.35 0.45;0.3 0.5;0.3 0.6;0.3 0.5;0.3 0.6;];
MxsDis=[%400 700 650 500 700 900 450 610 400 700
%650 500 700 900 450 610 700 900 450 610
500 700 300 350 700 900 450 610 450 610];
ytW = [%1 3 4 2 1 1 3 2 1 2
%3 2 1 3 2 1 2 3 2 1
1 1 1 1];
%这个数据里都代表的是目标点,是目标点与目标点的关系
MytTOrd=[3 2];
%引入新的协同矩阵,最大起始时间矩阵
Twait = [30 40 20 15 50 70 30 80 90 65];
Twindow=[];
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
if Key == 0
else if Key == 1
for i=1:20
DDE1 = DMDEAssignTarget(cTerrain,xs,yt,MxsEna,MxsDis,ytW,MytTOrd,Twait,Twindow,i);
% MC = Cal1.GetMcost();
%Cal1 = CallocationTargetOld1(cTerrain);
%标签显示文字
xlabel('X/km')
ylabel('Y/km')
zlabel('Z/km')
%DDEAssign1=DDEAssignTarget1(cTerrain,xs,yt,MxsEna,MxsDis,ytW,MytTOrd);
%执行run并返回结果集
t1 = cputime;
[solU solT solC solF ] = DDE1.run();
solu(i,:) = solU;
solt(i,:) = solT;
solc(i,:) = solC;
solf(i,:) = solF;
Time(i,:) = cputime -t1;
end %i
% %结果
solu
solt
solc
solf
Time
end % key=1
end % key=0
else if AssignType == 3
%% 第三种实验的情况
%%%%%%%%%%%%%%%%%%%%%%%数据区%%%%%%%%%%%%
xs = [%11 2 3;2 17 5; 34 26 7;5 2 2;6 33 3;27 34 6;21 45 5;25 12 3;22 17 11;13 31 12;
%45 21 11; 36 22 11;13 21 16;41 25 10;25 25 11;53 12 14;22 12 12;18 32 11; 67 34 12;26 16 15;
78 20 15;93 31 12;31 20 13;112 32 15];
yt = [%40 210 12;170 90 13 ; 80 197 21 ;172 120 13;160 56 13;160 143 21;170 200 21;113 200 12;97 134 16;100 145 11;
%81 101 21; 72 152 12; 133 60 11;84 164 21; 150 90 21;146 121 12; 167 54 12; 108 165 12;99 120 21;110 143 11;
70 131 12;15 133 13 ; 19 151 12 ;160 192 13;101 120 23;160 113 12;82 101 11;173 140 12;182 65 14; 45 176 12;];
MxsEna=[%0.2 0.3; 0.2 0.4;0.4 0.75;0.3 0.6;0.2 0.3;0.35 0.45;0.3 0.5;0.3 0.6;0.2 0.3; 0.2 0.4;
% 0.4 0.75;0.3 0.6;0.2 0.3;0.35 0.45;0.3 0.5;0.3 0.6;0.2 0.3;0.35 0.45;0.3 0.5;0.3 0.6;
0.2 0.5; 0.3 0.4;0.4 0.75;0.3 0.45];
MxsDis=[%400 700 650 500 700 900 450 610 400 700
%650 500 700 900 450 610 700 900 450 610
700 700 900 650];
ytW = [%1 3 4 2 1 1 3 2 1 2
%3 2 1 3 2 1 2 3 2 1
1 1 1 1 1 1 1 1 1 1];
MytTOrd=[3 4; 5 2];
%引入新的协同矩阵,最大起始时间矩阵
Twait = [30 40 20 15];
Twindow=[1300,6000];
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
if Key == 0
%%%%%%%%%%%%%%%%%%%%%%算法执行区%%%%%%%%%%%%%%%%%%
%调用目标分配算法,并取得解和相关数据,计算算法耗费时间
%定义目标分配算法对象
DDE1 = DMDEAssignTarget(cTerrain,xs,yt,MxsEna,MxsDis,ytW,MytTOrd,Twait,Twindow,1);
% MC = Cal1.GetMcost();
%Cal1 = CallocationTargetOld1(cTerrain);
%标签显示文字
xlabel('X/km')
ylabel('Y/km')
zlabel('Z/km')
%DDEAssign1=DDEAssignTarget1(cTerrain,xs,yt,MxsEna,MxsDis,ytW,MytTOrd);
%执行run并返回结果集
t1 = cputime;
[solU solT solC solF] = DDE1.run();
Time = cputime -t1;
% %结果
solU
solT
solC
solF
Time
else if Key == 1
for i=1:20
DDE1 = DMDEAssignTarget(cTerrain,xs,yt,MxsEna,MxsDis,ytW,MytTOrd,Twait,Twindow,i);
% MC = Cal1.GetMcost();
%Cal1 = CallocationTargetOld1(cTerrain);
%标签显示文字
xlabel('X/km')
ylabel('Y/km')
zlabel('Z/km')
t1 = cputime;
[solU solT solC solF ] = DDE1.run();
solu(i,:) = solU;
solt(i,:) = solT;
solc(i,:) = solC;
solf(i,:) = solF;
Time(i,:) = cputime -t1;
end %i
% %结果
solu
solt
solc
solf
Time
end % key=1
end % key=0
end % type =3
end % type =2
end % type=1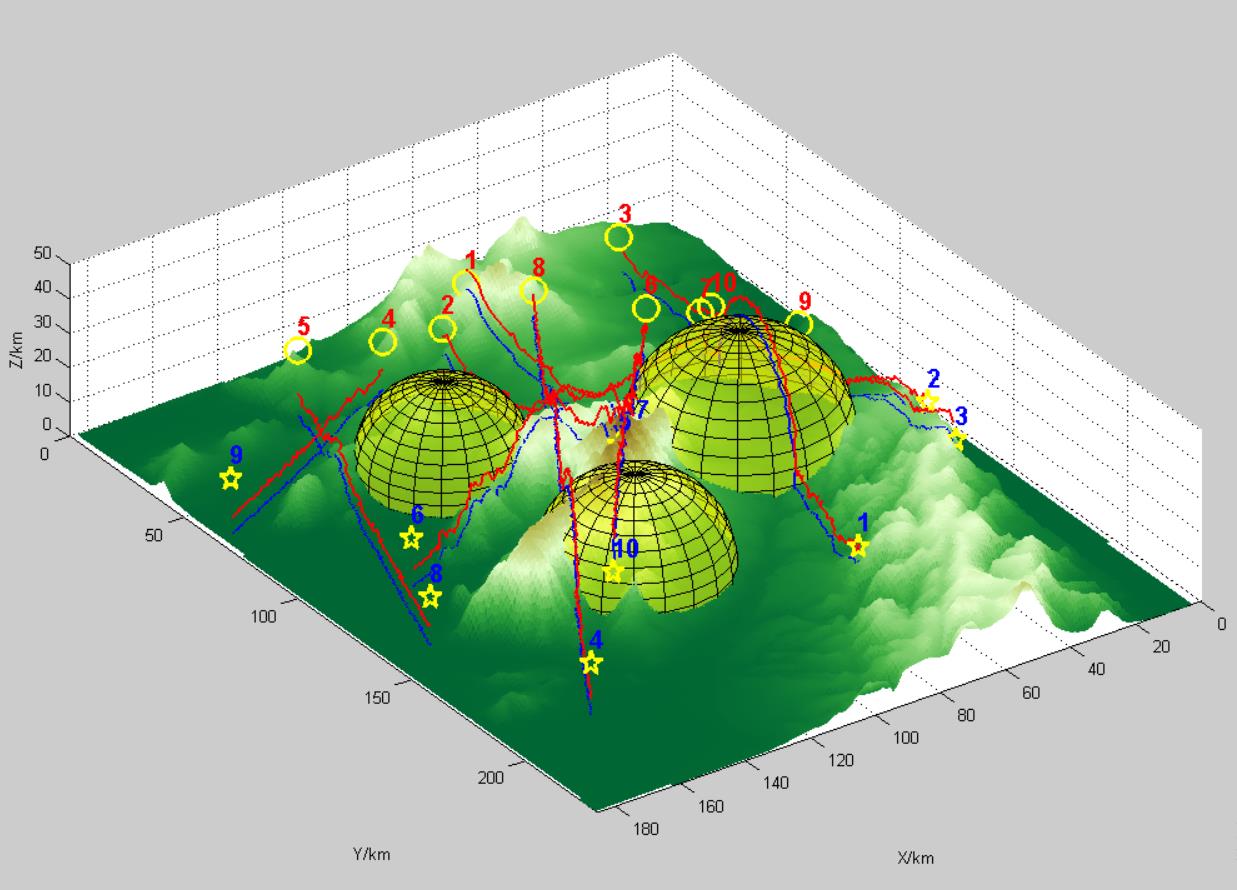
完整代码添加QQ1575304183
以上是关于路径规划基于改进差分算法实现三维多无人机协同航迹规划的主要内容,如果未能解决你的问题,请参考以下文章
三维路径规划基于matlab粒子群算法融合鸡群算法多无人机三维路径规划含Matlab源码 1792期
三维路径规划基于matlab粒子群算法无人机三维路径规划含Matlab源码 192期
三维路径规划基于matlab粒子群算法无人机山地三维路径规划含Matlab源码 1831期
三维路径规划基于matlab球面矢量粒子群算法无人机三维路径规划含Matlab源码 1682期