机器人路径规划基于粒子群之机器人栅格路径规划

Posted 2021-05-18 Matlab走起

​首先用栅格法描述机器人工作环境,在此基础上,将机器人路径表示为粒子位置的二进制编码,并以路径长度为适应值,产生初始种群后,再对粒子位置和速度进行更新,经过多次迭代,即可获得从起始点到目标点的一条全局最优路径.

clc;
close all
clear
load('data4.mat')
figure(1)%画障碍图
hold on
S=(S_coo(2)-0.5)*num_shange+(S_coo(1)+0.5);%起点对应的编号
E=(E_coo(2)-0.5)*num_shange+(E_coo(1)+0.5);%终点对应的编号
for i=1:num_shange
    for j=1:num_shange
        if sign(i,j)==1
            y=[i-1,i-1,i,i];
            x=[j-1,j,j,j-1];
            h=fill(x,y,'k');
            set(h,'facealpha',0.5)
        end
        s=(num2str((i-1)*num_shange+j));
        %text(j-0.95,i-0.5,s,'fontsize',6) 
    end
end
axis([0 num_shange 0 num_shange])%限制图的边界
plot(S_coo(2),S_coo(1), 'p','markersize', 10,'markerfacecolor','b','MarkerEdgeColor', 'm')%画起点
plot(E_coo(2),E_coo(1),'o','markersize', 10,'markerfacecolor','g','MarkerEdgeColor', 'c')%画终点
set(gca,'YDir','reverse');%图像翻转
for i=1:num_shange
    plot([0 num_shange],[i-1 i-1],'k-');
    plot([i i],[0 num_shange],'k-');%画网格线
end
PopSize=20;%种群大小
OldBestFitness=0;%旧的最优适应度值
gen=0;%迭代次数
maxgen =20;%最大迭代次数
​
c1=0.5;%认知系数
c2=0.7;%社会学习系数
w=0.96;%惯性系数
%%
%初始化路径
w_min=0.5;
w_max=1;
Group=ones(num_point,PopSize);  %种群初始化


​
%最优解
route=Group(:,end)';
index1=find(route==E);
route_lin=route(1:index1);
for i=2:index1
    Q1=[mod(route_lin(i-1)-1,num_shange)+1-0.5,ceil(route_lin(i-1)/num_shange)-0.5];
    Q2=[mod(route_lin(i)-1,num_shange)+1-0.5,ceil(route_lin(i)/num_shange)-0.5];
    plot([Q1(1),Q2(1)],[Q1(2),Q2(2)],'b-.','LineWidth',3);hold on
    
end
title('粒子群算法-随机路线');
​
title('粒子群算法-随机路线');
figure(2)
hold on
for i=1:num_shange
    for j=1:num_shange
        if sign(i,j)==1
            y=[i-1,i-1,i,i];
            x=[j-1,j,j,j-1];
            h=fill(x,y,'k');
            set(h,'facealpha',0.5)
        end
        s=(num2str((i-1)*num_shange+j));
        text(j-0.95,i-0.5,s,'fontsize',6) 
    end
end
axis([0 num_shange 0 num_shange])%限制图的边界
plot(S_coo(2),S_coo(1), 'p','markersize', 10,'markerfacecolor','b','MarkerEdgeColor', 'm')%画起点
plot(E_coo(2),E_coo(1),'o','markersize', 10,'markerfacecolor','g','MarkerEdgeColor', 'c')%画终点
set(gca,'YDir','reverse');%图像翻转
for i=1:num_shange
    plot([0 num_shange],[i-1 i-1],'k-');
    plot([i i],[0 num_shange],'k-');%画网格线
end
for i=2:index1
    Q1=[mod(route_lin(i-1)-1,num_shange)+1-0.5,ceil(route_lin(i-1)/num_shange)-0.5];
    Q2=[mod(route_lin(i)-1,num_shange)+1-0.5,ceil(route_lin(i)/num_shange)-0.5];
    plot([Q1(1),Q2(1)],[Q1(2),Q2(2)],'b-.','LineWidth',3)
end
%初始化粒子速度（即交换序）
Velocity =zeros(num_point,PopSize);   
for i=1:PopSize
    Velocity(:,i)=round(rand(1,num_point)'*num_point/10); %round取整
end
​
%计算每个个体对应路径的距离
for i=1:PopSize   
  EachPathDis(i) = PathDistance(Group(:,i)',E,num_shange);
end
​
IndivdualBest=Group;%记录各粒子的个体极值点位置,即个体找到的最短路径
IndivdualBestFitness=EachPathDis;%记录最佳适应度值,即个体找到的最短路径的长度
[GlobalBestFitness,index]=min(EachPathDis);%找出全局最优值和相应序号
%寻优
while gen < maxgen
    w=w_max-(w_max-w_min)*gen/maxgen;
    %迭代次数递增
    gen = gen +1
    %更新全局极值点位置,这里指路径
    for i=1:PopSize   
        GlobalBest(:,i) = Group(:,index);
    end
   
 
    for i = 1:PopSize    % 更新各路径总距离
        EachPathDis(i) = PathDistance(Group(:,i)',E,num_shange);
    end
    IsChange = EachPathDis<IndivdualBestFitness;%更新后的距离优于更新前的，记录序号
    IndivdualBest(:, find(IsChange)) = Group(:, find(IsChange));%更新个体最佳路径
    IndivdualBestFitness = IndivdualBestFitness.*( ~IsChange) + EachPathDis.*IsChange;%更新个体最佳路径距离
    [GlobalBestFitness, index] = min(IndivdualBestFitness);%更新全局最佳路径,记录相应的序号
​
    if GlobalBestFitness~=OldBestFitness %比较更新前和更新后的适应度值;
        OldBestFitness=GlobalBestFitness;%不相等时更新适应度值
        best_route=IndivdualBest(:,index)';
    end   
     BestFitness(gen) =GlobalBestFitness;%每一代的最优适应度
end
%最优解
index1=find(best_route==E);
route_lin=best_route(1:index1);
for i=2:index1
    Q1=[mod(route_lin(i-1)-1,num_shange)+1-0.5,ceil(route_lin(i-1)/num_shange)-0.5];
    Q2=[mod(route_lin(i)-1,num_shange)+1-0.5,ceil(route_lin(i)/num_shange)-0.5];
    plot([Q1(1),Q2(1)],[Q1(2),Q2(2)],'r','LineWidth',3)
end
for i=1:PopSize
    p_lin=randperm(num_point)';%随机生成1*400不重复的行向量
    %% 将起点编号放在首位
    index=find(p_lin==S);
    lin=p_lin(1);
    p_lin(1)=p_lin(index);
    p_lin(index)=lin;
    Group(:,i)=p_lin;
    %%将每个个体进行合理化处理
    [Group(:,i),flag]=deal_fun(Group(:,i),num_point,liantong_point,E,num_shange);
    while flag==1%如处理不成功，则初始化个体，重新处理
        p_lin=randperm(num_point)';
        index=find(p_lin==S);
        lin=p_lin(1);
        p_lin(1)=p_lin(index);
        p_lin(index)=lin;
        Group(:,i)=p_lin;
        [Group(:,i),flag]=deal_fun(Group(:,i),num_point,liantong_point,E,num_shange);       
    end
end
​
%最优解
route=Group(:,end)';
index3=find(route==E);
route_lin1=route(1:index3);
for i=2:index3
    Q1=[mod(route_lin1(i-1)-1,num_shange)+1-0.5,ceil(route_lin1(i-1)/num_shange)-0.5];
    Q2=[mod(route_lin1(i)-1,num_shange)+1-0.5,ceil(route_lin1(i)/num_shange)-0.5];
    plot([Q1(1),Q2(1)],[Q1(2),Q2(2)],'c-.','LineWidth',3);hold on
end
for i=1:PopSize
    p_lin=randperm(num_point)';%随机生成1*400不重复的行向量
    %% 将起点编号放在首位
    index=find(p_lin==S);
    lin=p_lin(1);
    p_lin(1)=p_lin(index);
    p_lin(index)=lin;
    Group(:,i)=p_lin;
    %%将每个个体进行合理化处理
    [Group(:,i),flag]=deal_fun(Group(:,i),num_point,liantong_point,E,num_shange);
    while flag==1%如处理不成功，则初始化个体，重新处理
        p_lin=randperm(num_point)';
        index=find(p_lin==S);
        lin=p_lin(1);
        p_lin(1)=p_lin(index);
        p_lin(index)=lin;
        Group(:,i)=p_lin;
        [Group(:,i),flag]=deal_fun(Group(:,i),num_point,liantong_point,E,num_shange);       
    end
end
​
%最优解
route=Group(:,end)';
index2=find(route==E);
route_lin2=route(1:index2);
for i=2:index2
    Q1=[mod(route_lin2(i-1)-1,num_shange)+1-0.5,ceil(route_lin2(i-1)/num_shange)-0.5];
    Q2=[mod(route_lin2(i)-1,num_shange)+1-0.5,ceil(route_lin2(i)/num_shange)-0.5];
    plot([Q1(1),Q2(1)],[Q1(2),Q2(2)],'m-.','LineWidth',3);hold on
end
title('粒子群算法-对比路线');
figure(3)
hold on
for i=1:num_shange
    for j=1:num_shange
        if sign(i,j)==1
            y=[i-1,i-1,i,i];
            x=[j-1,j,j,j-1];
            h=fill(x,y,'k');
            set(h,'facealpha',0.5)
        end
        s=(num2str((i-1)*num_shange+j));
        text(j-0.95,i-0.5,s,'fontsize',6) 
    end
end
axis([0 num_shange 0 num_shange])%限制图的边界
plot(S_coo(2),S_coo(1), 'p','markersize', 10,'markerfacecolor','b','MarkerEdgeColor', 'm')%画起点
plot(E_coo(2),E_coo(1),'o','markersize', 10,'markerfacecolor','g','MarkerEdgeColor', 'c')%画终点
set(gca,'YDir','reverse');%图像翻转
for i=1:num_shange
    plot([0 num_shange],[i-1 i-1],'k-');
    plot([i i],[0 num_shange],'k-');%画网格线
end
for i=2:index1
    Q1=[mod(route_lin(i-1)-1,num_shange)+1-0.5,ceil(route_lin(i-1)/num_shange)-0.5];
    Q2=[mod(route_lin(i)-1,num_shange)+1-0.5,ceil(route_lin(i)/num_shange)-0.5];
    plot([Q1(1),Q2(1)],[Q1(2),Q2(2)],'r','LineWidth',3)
end
title('粒子群算法-最优路线');
​
​
%进化曲线
figure(4);
plot(BestFitness);
xlabel('迭代次数')
ylabel('适应度值')
grid on;
title('进化曲线');
disp('粒子群算法-最优路线方案：')
disp(num2str(route_lin))
disp(['起点到终点的距离:',num2str(BestFitness(end))]);
figure(5);
plot(BestFitness*100);
xlabel('迭代次数')
ylabel('适应度值')
grid on;
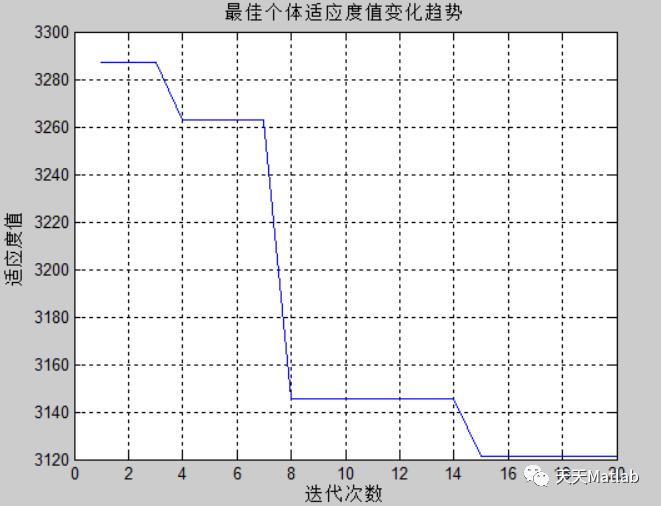
title('最佳个体适应度值变化趋势');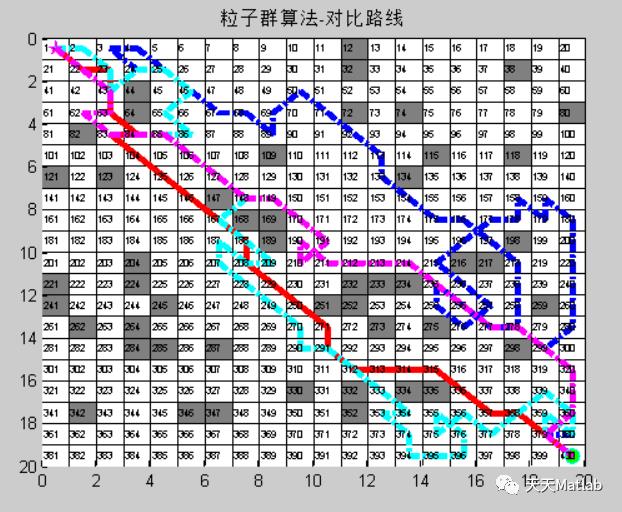

 

完整代码添加QQ1575304183