C#基础搜索算法

Posted 2021-05-18 苏州程序大白

C#基础搜索算法

大家好，我是苏州程序大白。下面讲讲C#中基础搜索算法。
数据搜索是基础的计算机编程工作, 而且人们对它的研究已经很多年了. 本章只会看到搜索问题的一个内容, 即根据给定的数值在一个列表（数组）中进行搜索. 有两种对列表内数据进行搜索的方法：顺序搜索和二叉搜索. 当数据项在列表内随机排列的时候可以使用顺序搜索, 而当数据项在列表内有序排列的时候则会用到二叉搜索。

顺序搜索算法

最直接的搜索类型就是从数据的开始处顺次遍历每条记录, 直到找到所要的记录或者是到达数据的末尾. 这就是所谓的顺序搜索.
顺序搜索（也被称为线性搜索）是非常容易实现的. 从数组的起始处开始, 把每个访问到的数组元素依次和所要搜索的数值进行比较. 如果找到匹配的数据项, 就结束搜索操作. 如果 遍历到数组的末尾仍没有产生匹配, 那么就说明此数值不在数组内.
下面是一个执行顺序搜索操作的函数：

bool SeqSearch(int[] arr, int sValue) 
{ 
    for (int index = 0; index < arr.Length ; index++) 
        if (arr[index] == sValue) 
            return true; 
    return false; 
} 

如果发现匹配, 那么函数会立刻返回True并且退出. 如果到达数组的末尾, 函数还没有返回True, 那么要搜索的数值就不在数组内, 而函数则会返回False.
下面这个程序用来测试顺序搜索的实现：

using System;

public class Chapter4 {
    static void Main()
    {
        int[] numbers = new int[100];
        //原文代码的例子要读取一个txt文件里的数字 我给简化了
        for (int i = 0; i < numbers.Length; i++) 
            numbers[i] = i;
        int searchNumber;
        Console.Write("输入要查找的数: ");
        searchNumber = Convert.ToInt32(Console.ReadLine(), 10);//第二个参数10指的按照10进制转换
        Console.WriteLine(searchNumber);
        bool found;
        found = SeqSearch(numbers, searchNumber);
        if (found)
            Console.WriteLine(searchNumber + " 找到了");
        else
            Console.WriteLine(searchNumber + " 没找到");
        Console.ReadLine();
    }

    static bool SeqSearch(int[] arr, int sValue)
    {
        for (int index = 0; index < arr.Length; index++) //小bug 
            if (arr[index] == sValue)
                return true;
        return false;
    }
}

程序首先会通过从文本文件中读取一组数据开始运行. 数据是由前100 个整数组成的, 而且是按照部分随机的顺序进行存储的. 随后, 程序会提示用户输入所要搜索的数, 并且调用SeqSearch函数来进行搜索.
当然, 用户也可以改写SeqSearch函数, 使其找到要搜索的元素时, 返回此数值在数组内的索引. 而当没有找到要搜索的数值时, 让函数返回-1. 首先来看一看如此修改后的SeqSearch函数：

static int SeqSearch(int[] arr, int sValue) 
{ 
    for (int index = 0; index < arr.Length ; index++) //小bug 
        if (arr[index] == sValue) 
            return index; 
    return -1; 
} 

下面这段代码使用了修改后的SeqSearch函数 :

using System; 

public class Chapter4 
{ 
    static void Main() 
    { 
        int[] numbers = new int[100]; 
        //原文代码的例子要读取一个txt文件里的数字 我给简化了
        for (int i = 0; i < numbers.Length; i++) 
            numbers[i] = i;
        int searchNumber; 
        Console.Write("输入要查找的数: "); 
        searchNumber = Convert.ToInt32(Console.ReadLine(), 10); 
        int foundAt; 
        foundAt = SeqSearch(numbers, searchNumber); 
        if (foundAt >= 0) 
            Console.WriteLine(searchNumber + "在位置"  + foundAt); 
        else 
            Console.WriteLine(searchNumber + "没找到"); 
        Console.ReadLine();
    } 
    static int SeqSearch(int[] arr, int sValue) 
    { 
        for (int index = 0; index < arr.Length ; index++) 
            if (arr[index] == sValue) 
                return index; 
        return -1; 
    } 
} 

搜索最小值和最大值

人们经常要求计算机程序从数组（或者其他数据结构）里搜索到最小值或最大值. 在一个有 序的数组中, 搜索最小值和最大值是很容易的工作. 但是, 在一个无序的数组中, 这就是一 个不小的挑战了.
下面就从找到数组的最小值开始吧. 算法是：
ⅰ. 把数组的第一个元素作为最小值赋值给一个变量.
ⅱ. 开始循环遍历数组, 并且把每一个后继数组元素与最小值变量进行比较.
ⅲ. 如果当前访问到的数组元素小于最小值, 就把此元素赋值给最小值变量.
ⅳ. 继续上述操作直到访问到最后一个数组元素为止.
ⅴ. 最小值就是存储在变量内的数值了.
下面来看看实现此算法的函数FindMin：

static int FindMin(int[] arr) 
{ 
    int min = arr[0]; 
    for(int i = 0; i < arr.Length-1; i++) 
        if (arr[index] < min) 
            min = arr[index]; 
    return min; 
} 

请注意数组搜索是从第1 个元素的位置开始的, 而不是从第0 个元素的位置开始. 第0 个元素的位置在循环开始前会作为初始的最小值, 因此进行循环比较的操作从第1 个元素开始.
在数组内搜索最大值的算法和搜索最小值的方法相同. 先把数组的首元素赋值给一个保存最大值的变量. 接着循环遍历数组, 把每个数组元素与存储在变量内的数值进行比较. 如果访 问到的数值大于当前, 就进行替换. 下面是代码：

static int FindMax(int[] arr) 
{ 
    int max = arr[0]; 
    for(int i = 0; i < arr.Length-1; i++) 
        if (arr[index] > max) 
            max = arr[index]; 
    return max; 
} 

上述两个函数的另外一种可选写法是返回最大值或最小值在数组内的位置, 而不是返回实际的数值。

通过自组织数据加快顺序搜索速度

当要搜索的数据元素在数据集合的开始处时, 搜索过程就能够以最快的速度完成. 那么为了优化多次搜索过程的效率, 可以在找到目标元素后把它移动到数据的靠前的位置 提高下一次搜索它们的速度.
这种策略的目的就是通过把频繁搜索的数据项放在数据开始处来最小化搜索一个元素所需要的循环次数. 随着多次查询的进行, 最终的结果就是最频繁被搜索的元素都会被放置在开始部分. 这是就是所谓"自组织数据"的一个例子, 数据不是在程序运行之前由程序员组织的, 而是在程序运行期间由程序自身组织的.
要搜索的数据多数时候会遵循“2-8”规律, 指的是80%的搜索操作都是为了搜索到20%的那部分的数据. 自组织将最终把20%的部分放在数据的开始的位置, 这样顺序搜索就可以快速找到它们.
像这样的概率分布被称为是帕累托分布(Pareto distributions), 它是以19 世纪后期通过研究收入和财富的扩散而发现这个概率分布规律的科学家Vilfredo Pareto的名字命名的. 更多有关数据中概率分布的知识请参阅Knuth 的书 (1998, pp. 399–401 全书校对完我会把参考书目单独建一篇文档).
回到之前的代码, SeqSearch可以很容易的实现自组织特性. 修改代码如下 ：

//可以放在第三章做的CArry类里
int SeqSearch(int sValue) 
{ 
    for(int index = 0; index < arr.Length-1; index++) 
        if (arr[index] == sValue) 
        { 
            //通过位置交换函数, 将被搜索的元素位置提前
            swap(index);          
            return index; 
        }     
    return -1; 
} 

如果搜索成功, 则使用swap函数把找到的数据项与第一个位置的元素交换位置, swap函数代码如下：

//可以放在第三章做的CArry类里
void swap(int index1, int index2)
{
    //指定元素与第一个元素交换
    int temp = arr[index];
    arr[index] = arr[0];
    arr[0] = temp;
}

上述代码实现的数据自组织功能, 存在两个问题 : 第一个问题是, 每次搜索都会将第一个元素位置替换掉, 也就是说, 始终只有一个被搜索的元素位置得到了搜索优化, 而且会在搜索其他元素时直接被替换掉; 第二个问题是, 每次搜索必定会进行元素位置交换, 需要调用交换方法和使用中间变量, 性能开销较多
我们实际希望数据自组织可以做到的效果是 :

1. 越频繁搜索的元素位置越靠前, 而不是每次都将其放置到第一位
2. 已经比较靠前面的元素, 其搜索速度已经可以接受, 不需要再进行自组织优化了, 减少数据交换带来的不必要开销
   根据以上思路, 对于第一点, 我们可以使用类似冒泡排序的方式, 将一个搜索到的元素移动到第一个位置, 而不是直接与第一个元素交换, 这样虽然第一个元素还是会被替换, 但是他实际移动到了第二个位置, 而不是直接被交换到了后面的某个位置 ; 对于第二点, 结合本节前面提到的2-8法则, 可以只对位置远与前20%部分的元素才进行自组织优化, 否则不需要改变被搜索元素的位置, 实现代码如下 :

//CArray类中的函数代码

public int SeqSearch(int sValue)
{
    for (int index = 0; index < arr.Length; index++) {            
        if(arr[index] == sValue) {
            //如果搜到了, 还需要检查是否远于指定位置,                 
            if (index > arr.Length * 0.2) {
                //如果远于指定位置, 则进行数据自组织交换优化
                swap(index);
                //优化后始终位于第一位
                return 0;
            }
            else if (arr[index] == sValue)
                //如果已经比较靠前, 搜索速度可以接受, 不进行自组织优化, 直接返回索引
                return index;
        }            
    }
    return -1;
}

//数组自组织优化方法
void swap(int index)
{
    int temp = arr[index];
    //类似冒泡排序的移动方法, 接将指定位置的元素冒泡到第一位
    for (int i = index; i > 0; i--) {
        arr[i] = arr[i - 1];
    }
    arr[0] = temp;
}

之后我们在Main函数中使用1到10的数字初始化一个CArray对象, 代码如下 :

using System;

public class Chapter4 {
    static void Main()
    {
        int resultIndex;
        CArray ca = new CArray(10);
        for (int i = 0; i < 10; i++) {
            ca.Insert(i);
        }
        while (true) {
            Console.Write("输入你要搜索的数据: ");
            resultIndex = ca.SeqSearch(int.Parse(Console.ReadLine()));
            if (resultIndex == -1)
                Console.WriteLine("啥也没找到哭唧唧");
            else
                Console.WriteLine($"在索引{resultIndex}找到了!");
            ca.DisplayElements();
        }
    }
}

运行参考结果如下 :

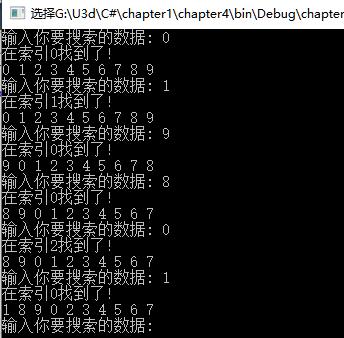
(分界索引计算用的数组长度*0.2, 所以是2而不是1, 也就是你会看到, 前三个元素都不会触发自组织优化)
以上方法对于可以帮助你更好的对无序的数据集合进行搜索. 下面一节中要介绍的搜索算法比顺序搜索算法高效得多, 但只能用来搜索有序的数据集合,它就是二叉搜索算法。

二叉搜索算法

当要搜索的记录从头到尾有序排列时, 可以执行一种比顺序搜索更加有效的搜索算法, 称为是二叉搜索.
为了理解二叉搜索的工作原理, 请假设你正试图猜测由朋友选定的一个在1 至100 之间的数字. 对于每次你所做的猜测, 朋友都会告诉你是猜对了, 还是猜大了, 或是猜小了. 最好的策略是第一次猜50. 如果猜大了, 那么就应该再猜 25. 如果猜 50 猜小了, 则应该再猜75. 在每次猜测的时候, 你都应该根据调整的数的较小或较大范围（这依赖于你猜测的数是偏大还是偏小）选择一个新的中间点作为下次要猜测的数. 只要遵循这个策略, 你最终一定会猜出正确的数. 图4-1 说明了如果选择的数是82 时这个策略的工作过程。

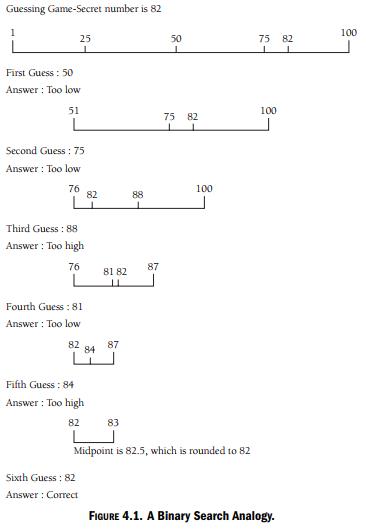
可以把这种策略作为一种算法来实现, 即二叉搜索算法. 为了使用这种算法, 首先需要 把数据按顺序（最好是升序方式）存储到数组内（当然, 其他数据结构也可行）. 算法的第 一步就是设置搜索的上界和下界. 在搜索刚开始时, 就是数组的上限和下限. 然后, 通过把上限和下限相加后除以2 的操作就可以计算出数组的中间索引点. 接着把存储在中间点上的数组元素与要搜索的数值进行比较. 如果两者相同, 那么就表示找到了该数值, 同时查 找算法也就此结束. 如果要搜索的数值小于中间点的值, 那么就通过从中间点减去一的操作 计算出新的上限. 否则, 若是要搜索的数值大于中间点的值, 那么就把中间点加一求出新的下限. 此算法反复执行直到下限和上限相等时终止, 这也就意味着已经对数组全部搜索完了.
如果搜索结束, 也没有找到适合的元素就返回-1, 这表示数组中不存在要搜索的数值. 这里把算法作为C#函数进行了编写：

//可以放在CArray类中
public int binSearch(int value)
{
    int upperBound, lowerBound, mid;
    //上限索引初始为最后一个索引
    upperBound = arr.Length - 1;
    //下限索引初始为第一个索引
    lowerBound = 0;
    //一直搜索到上下限索引重合
    while (lowerBound <= upperBound) {
        //寻找中间点位置
        mid = (upperBound + lowerBound) / 2;
        Console.Write($"搜索第{mid}位...");
        if (arr[mid] == value) {
            //搜索到元素后返回索引
            Console.WriteLine();
            return mid;
        }
        else if (value < arr[mid])
            //本轮没搜索到, 如果搜索的值偏小, 则将中间索引前面的索引作为新的上限
            upperBound = mid - 1;
        else
            //本轮没搜索到, 如果搜索的值偏大会, 则将中间索引后面的索引作为新的下限
            lowerBound = mid + 1;
    }
    //执行到这里表示没找到
    Console.WriteLine();
    return -1;
}

使用下面的Main函数来调用二叉搜索函数演示搜索效果 :

//我自己改写的, 原文代码有问题, 使用的二叉搜索函数带三个参数
//我猜这本书的代码很可能是多人或多次, 不同时间书写的, 而出版编辑又没用实际运行测试, 错误频出
using System;

public class Chapter4 {
    static void Main()
    {
        int temp = 1000;
        CArray ca = new CArray(temp);
        Random rnd = new Random();
        for (int i = 0; i < temp; i++) {
            ca.Insert(i + rnd.Next(3));
        }
        while (true) {
            Console.Write("输入你要搜索的数据: ");
            temp = ca.binSearch(int.Parse(Console.ReadLine()));
            if (temp == -1)
                Console.WriteLine("===啥也没找到哭唧唧===");
            else
                Console.WriteLine($"===在索引{temp}找到了!===");
        }
    }
}

运行效果如下 :

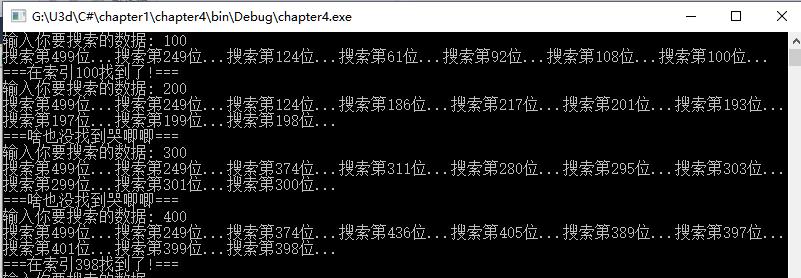
递归二叉搜索算法

尽管上节中的二叉搜索算法函数可以正确工作, 但它其实不是解决类似搜索问题的常规方案. 二叉搜索函数可以使用递归方式实现(递归指函数的内部调用自身), 这是因为此算法会不断地划分数组直到找到所要的数据项或搜索完全部数组才会终止, 而每次的划分都是会得到一个新的范围更小的数据集合, 因此非常适合使用递归来实现二叉搜索算法.
递归二叉搜索函数的代码将在上节的二叉搜索函数基础上进行一些改动, 下面先来看一下新的函数代码, 然后再讨论已经修改的内容 ：

//后两个参数让你手动指定在数据的哪一段执行二叉搜索
public int RbinSearch(int value, int lower, int upper) 
{ 
    //如果下限大于上限了, 说明已经全部搜索完成, 没有找到目标数据
    if (lower > upper) 
        return -1; 
    else 
    { 
        int mid; 
        mid = (int)(upper+lower) / 2; 
        if (value < arr[mid]) 
            //将原来循环迭代的方式, 改成递归的方式, 使用新的搜索范围作为参数再次调用自身
            return RbinSearch(value, lower, mid - 1); 
        else if (value == arr[mid]) 
            return mid; 
        else 
            //将原来循环迭代的方式, 改成递归的方式, 使用新的搜索范围作为参数再次调用自身
            return RbinSearch(value, mid + 1, upper); 
    } 
} 

同迭代算法相比, 递归二叉搜索算法的主要问题是它的效率. 当用这两种算法对含有1000个元素的数组进行排序的时候, 递归算法始终比迭代算法慢了10 倍：

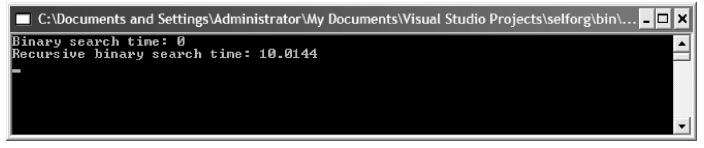
(我的电脑太快了…我换了条件测试的结果如下, 以供参考)

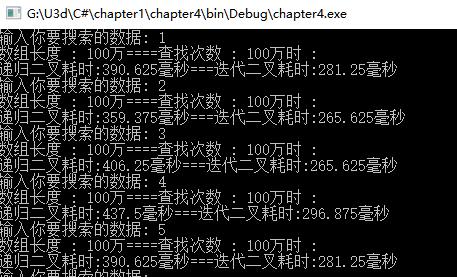
可以看到, 递归方式的二叉搜索比迭代的方式要慢, 不过尽管这样, 在解决实际问题时可能是出于性能的考虑之外才选择的递归算法(不太赞同, 主要原因还是要看效率, 只不过恰好对于这个例子的需求来说, 递归效率差. 关于递归与迭代差异的原因可以看看为什么递归效率比迭代差那么多). 而你需要记在心里的就是, 任何时候当你想使用递归, 你都需要考虑甚至实际对比下与迭代方式实现同样功能的性能差异
最后在结束二叉搜索这个主题之前, 还应该提到Array类所拥有的内置的二叉搜索方法. 此 方法需要两个参数, 即数组名和要搜索的数据项. 然后, 它会返回该数据项在数组内的位置, 或者是由于没找到而返回-1.
为了说明此方法的工作原理, 这里为所提及的类另外写了一个二叉搜索方法. 代码如下所示：

public int Bsearh(int value) 
{ 
    return Array.BinarySearch(arr, value); 
} 

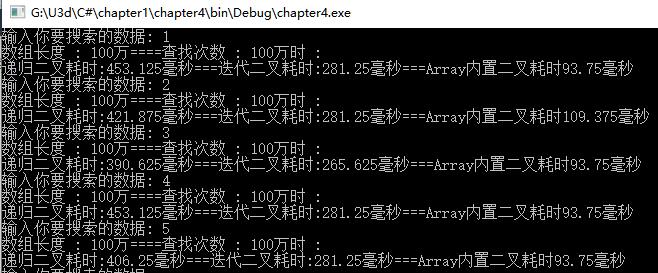
当内置的二叉搜索方法与用户定制的方法进行比较的时候, 内置方法始终比用户定制方法执行速度快很多. 这没什么好惊讶的. 在真正的工作环境下, 如果有内置的方法或数据结构可以满足需要, 那么应该始终优先选择内置的数据结构或算法而非用户定制的, 我们在本书中实现的自定义数据结构和算法更多的意义在于学习背后的原理.
(我也对比了下, 自行体会吧)

关注苏州程序大白，持续更新技术分享。谢谢大家支持