matlab遗传算法求解冷链路径优化问题

Posted 2021-05-18 张叔zhangshu

冷链描述

随着人民生活水平的不断提高和消费观念的不断转变，人们对生鲜农产品的需求量不断加大，对生鲜农产品的品质和时效要求也越来越严格。而生鲜农产品保鲜时间短、易腐性高的特点要求其在运输、储存、配送等环节中始终需要依托于低温的冷链
物流网络，这也导致了冷链配送成本始终居高不下。此外，在生鲜农产品的城市配送过程中，由于投入资本、区域规划、城市地价等因素的影响，企业一般将配送中心设置在远离市中心的郊区，但其的客户如超市、餐饮店、便利店等大多都在人流量集中的市中心区域，因此如何合理规划配送路径，以尽可能低的成本和尽可能高的服务质量满足客户需求，解决“最后一公里”配送难题便显得尤为重要。
而生鲜农产品配送路径优化问题的核心便是车辆路径问题（VRP），其是由美国学者Dantzig和Ramser在1959年首次提出[1]，此问题的经典描述是有一个配送中心和多个客户需求节点，在其地理位置和需求量等相关参数值都已知的情况下，如何在满足约束条件的前提下，找到一条最佳配送路径，使得其既可以满足全部的客户需求节点，又可以实现成本最低或路径最短的目标。此问题一经提起，便引发了诸多学者关注。近年来相关学者对其的研究主要集中在模型构建和算法求解等方面。范厚明等针对模糊需求与模糊时间窗的车辆路径问题，以总行驶距离、车辆使用数最小化以及平均客户满意度最大化为目标构建基于可信性测度理论的多目标模糊机会约束模型[2]。何小峰等针对蚁群算法在求解VRPTW问题时易陷入局部最优和收敛速度慢的问题，结合量子计算提出了一种量子蚁群算法（QACA），并通过仿真实验证明了该算法的有效性[3]。葛显龙等针对多车型车辆路径问题，建立以配送费用最小化为目标的数学模型，并采用量子比特位设计染色体结构，提出了一种改进的遗传算法求解模型[4]。张群等针对多车型、多配送中心、多产品的车辆路径问题，提出了一种新的模糊遗传算法，并通过标准算例对比，证明模糊遗传算法具有较好的计算结果和效率[5]。
综合上述分析，目前相关学者在车辆路径问题（VRP）上的研究已较为成熟，但将生鲜冷链物流与VRP相结合进行研究的文献相对较少。因此，本文在此将生鲜农产品冷链物流与VRP相结合，在车辆路径问题的基础上，考虑生鲜农产品以及冷链物流的特性，以总配送成本最小化为目标构建配送路径规划模型，并采用遗传算法对模型进行求解。
1 问题描述
在B2B城市冷链配送模式下，供应商一般会先将生鲜农产品运至配送中心，而后由配送中心再将生鲜农产品配送至线下的超市、餐饮店等，具体如图1。本文在此主要研究的是单一配送中心、单一车型的生鲜农产品配送路径优化问题。也就是说，只有一个配送中心为若干个分散在各地的客户节点提供配送服务，并且配送中心和客户节点的位置已知，不同客户节点对货物的需求量和期望接受的服务时间已知，如果配送车辆不能在客户期望的时间范围内提供服务便会产生一定的惩罚成本。此时，要求配送中心在不重复配送且客户需求都能满足的前提下，以尽可能低的成本，制定出高效合理的车辆配送方案。

（1）配送中心的冷链物流运输车辆充足且车型相同；
（2）客户的位置和需求量信息已知，且短时间内不会发生变动；
（3）每条线路上客户总需求量不得超过单车最大运载力，且每个客户只由一辆车服务；
（4）配送车辆一旦完成线路配送任务后便直接返回配送中心，即只考虑单程配送问题；
（5）客户对货物到达时间有一定要求，不在指定时间窗内完成配送将产生惩罚成本；
（6）货物在运输途中温度条件恒定且适宜，即只考虑时间因素带来的货损成本；
（7）车辆到达客户节点后装卸货物的时间忽略不计；
（8）冷链车辆在配送过程中匀速行驶，且道路交通和天气状况良好；
（9）所有客户节点的需求都能被满足。
本文在此采用遗传算法对优化模型进行求解，遗传算法是通过模拟生物进化理论而产生的一种具有自适应性的全局优化算法。遗传算法的基本流程如下：
（1）根据问题特点选择合适的编码策略；
（2）随机生成初始种群，并确定初始种群规模；
（3）确定适应度函数，适应度函数的取值代表个体优良性以及参与繁衍后代的概率；
（4）选择操作，按染色体适应度值的高低进行选择，适应度值越高的个体越容易生存和繁殖；
（5）交叉操作，将两个父代染色体中的基因按照一定规则进行互换，生成子代染色体；
（6）变异操作，按照一定的规则对染色体某个位置上的基因进行改变；
（7）不断进行迭代和遗传操作，直至达到最大迭代次数或适应度值不再改变后算法终止。
本文在此根据遗传算法的操作流程对算法进行设计。
3.1 编码设计
在此结合冷链物流配送路径优化问题的特点，为减少无效解的生成，对染色体采用自然数编码的方法进行编码操作，具体方法为:
（1）将n个客户节点依次编码为1,2，…n，将配送中心编码为0；
（2）随机无重复的对n个客户节点进行排列得到一条编码串，在编码串的初始位置插入0编码；
（3）按照配送车辆的载重限制等约束条件将0编码插入编码串中。
此时，相邻两个0编码之间的客户节点组成一条子路径，表示冷链车辆从配送中心出发为该条路径上的客户进行配送服务，完成配送服务后再返回配送中心。子路径中的染色体编码顺序代表着客户节点被服务的顺序，子路径的数量即为冷链车辆数。例如染色体“0357012804960”表示由三辆车完成9个客户节点的配送服务，分别对应着三条子路径，分别是：
 子路径1：0 3 5 7 0
 子路径2：0 1 2 8 0
 子路径3：0 4 9 6 0
3.2 生成初始种群
遗传算法初始种群的产生一般是随机的，种群规模太大会使计算效率降低，规模太小容易陷入局部最优。本文设计的种群生成办法如下：
（1）设定初始种群规模；
（2）随机排列n个客户节点并依次插入染色体；
（3）根据单车载重量插入0编码，得到初始染色体；
（4）重复2、3操作直至达到预定种群规模。
3.3 设置适应度函数
在遗传算法中，适应度函数用来评判种群中每个个体的优劣程度，适应度值越大，个体遗传到下一代的概率就越大。本文在此以配送成本最小化为目标，因此在构建适应度函数时，选取目标函数的倒数作为适应度函数，即： 。
3.4 遗传算子设计
（1）选择算子
在此采用遗传算法比较常用的“轮盘赌”选择策略，轮盘赌通过计算个体适应度值的大小决定个体被选中的概率。假设种群规模为 ，个体 的适应度值为 ，则个体 被选中的概率为： 。

（2）交叉算子
在此采用类似部分匹配交叉（PMX）的方式，它可以使得算法随机搜索机制更好遍历所有客户节点，并且可以快速找到最优解[6]，以下举例说明PMX的操作过程：

（3）变异算子
在此采用逆转变异的方式，即在个体中随机选取两个点位进行逆转变异操作，以得到一个新的个体，逆转变异操作过程如下：

3.5 算法终止条件
由于遗传算法是随机搜索算法，无法得到精确解，为防止其无限循环，需要设置相应终止条件使其循环迭代停止。在此选用常见的设置最大迭代次数作为算法终止的条件，当算法迭代到设置的最大迭代次数时便停止。

主程序

clear
clc
close all
tic
%% 用importdata这个函数来读取文件
% shuju=importdata('cc101.txt');
load('cc101');
shuju=c101;
% bl=importdata('103.txt');
bl=0;
cap=795;                                                        %车辆最大装载量
%% 提取数据信息

E=shuju(1,5);                                                    %配送中心时间窗开始时间
L=shuju(1,6);                                                    %配送中心时间窗结束时间
zuobiao=shuju(:,2:3);                                       %所有点的坐标x和y
% vertexs= vertexs./1000;
customer=zuobiao(2:end,:);                                       %顾客坐标
cusnum=size(customer,1);                                         %顾客数
v_num=6;                                                        %车辆最多使用数目
demands=shuju(2:end,4);                                          %需求量
a=shuju(2:end,5);                                                %顾客时间窗开始时间[a[i],b[i]]
b=shuju(2:end,6);                                                %顾客时间窗结束时间[a[i],b[i]]
s=shuju(2:end,7);                                                %客户点的服务时间
h=pdist(zuobiao);
% dist=load('dist1.mat');
% dist=struct2cell(dist);
% dist=cell2mat(dist);
% dist=dist./1000;                                               %实际城市间的距离
dist=squareform(h);  
dist=dist./1000;  %距离矩阵，满足三角关系，暂用距离表示花费c[i][j]=dist[i][j]
%% 遗传算法参数设置
alpha=100000;                                                       %违反的容量约束的惩罚函数系数
belta=40;%违反时间窗约束的惩罚函数系数
belta2=30;
chesu=55;

NIND=300;                                                       %种群大小
MAXGEN=100;                                                     %迭代次数
Pc=0.9;                                                         %交叉概率
Pm=0.05;                                                        %变异概率
GGAP=0.9;                                                       %代沟(Generation gap)
N=cusnum+v_num-1;                                %染色体长度=顾客数目+车辆最多使用数目-1
% N=cusnum;
%% 初始化种群
init_vc=init(cusnum,a,demands,cap);                             %构造初始解
Chrom=InitPopCW(NIND,N,cusnum,init_vc);
%% 输出随机解的路线和总距离
disp('初始种群中的一个随机值:')

[VC,NV,TD,violate_num,violate_cus]=decode(Chrom(1,:),cusnum,cap,demands,a,b,L,s,dist,chesu,bl);
% disp(['总距离：',num2str(TD)]);
disp(['车辆使用数目：',num2str(NV),'，车辆行驶总距离：',num2str(TD)]);
disp('~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~')
%% 优化
gen=1;
figure;
hold on;box on
xlim([0,MAXGEN])
title('优化过程')
xlabel('代数')
ylabel('最优值')
ObjV=calObj(Chrom,cusnum,cap,demands,a,b,L,s,dist,alpha,belta,belta2,chesu,bl);             %计算种群目标函数值
preObjV=min(ObjV);
while gen<=MAXGEN
    %% 计算适应度
    ObjV=calObj(Chrom,cusnum,cap,demands,a,b,L,s,dist,alpha,belta,belta2,chesu,bl);             %计算种群目标函数值
    line([gen-1,gen],[preObjV,min(ObjV)]);pause(0.0001)%画图 最优函数
    preObjV=min(ObjV);
    FitnV=Fitness(ObjV);
    %% 选择
    SelCh=Select(Chrom,FitnV,GGAP);
    %% OX交叉操作
    SelCh=Recombin(SelCh,Pc);
    %% 变异
    SelCh=Mutate(SelCh,Pm);
    %% 局部搜索操作
%     SelCh=LocalSearch(SelCh,cusnum,cap,demands,a,b,L,s,dist,alpha,belta,belta2,chesu,bl);
    %% 重插入子代的新种群
    Chrom=Reins(Chrom,SelCh,ObjV);
    %% 删除种群中重复个体，并补齐删除的个体
    Chrom=deal_Repeat(Chrom);
    %% 打印当前最优解
    ObjV=calObj(Chrom,cusnum,cap,demands,a,b,L,s,dist,alpha,belta,belta2,chesu,bl);             %计算种群目标函数值
    [minObjV,minInd]=min(ObjV);
    disp(['第',num2str(gen),'代最优解:'])
    [bestVC,bestNV,bestTD,best_vionum,best_viocus]=decode(Chrom(minInd(1),:),cusnum,cap,demands,a,b,L,s,dist,chesu,bl);
    disp(['车辆使用数目：',num2str(bestNV),'，车辆行驶总距离：',num2str(bestTD)]);
    fprintf('\\n')
    %% 更新迭代次数
    gen=gen+1 ;
end
%% 画出最优解的路线图
ObjV=calObj(Chrom,cusnum,cap,demands,a,b,L,s,dist,alpha,belta,belta2,chesu,bl);             %计算种群目标函数值
[minObjV,minInd]=min(ObjV);
%% 输出最优解的路线和总距离
disp('最优解:')
bestChrom=Chrom(minInd(1),:);
% bestChrom=[1,2,3,4,27,5,6,7,8,9,10,28,11,12,13,14,15,29,16,17,18,19,20,21,30,22,23,24,25,26,31]
% bestChrom=[30,7,17,19,3,5,1,25,14,29,27,4,18,15,6,12,9,28,11,23,22,24,20,2,13,21,8,26,16,10,31]
[bestVC,bestNV,bestTD,best_vionum,best_viocus]=decode(bestChrom,cusnum,cap,demands,a,b,L,s,dist,chesu,bl);
disp(['车辆使用数目：',num2str(bestNV),'，车辆行驶总距离：',num2str(bestTD)]);
disp('-------------------------------------------------------------')
[bestcost,gdcb,bdcb,zlcb,hscb,cfcb]=costFuction(bestVC,a,b,s,L,dist,demands,cap,alpha,belta,belta2,chesu,bl);
disp(['总成本：',num2str(bestcost)]);
disp(['固定成本：',num2str(gdcb)]);
disp(['变动成本：',num2str(bdcb)]);
disp(['制冷成本：',num2str(zlcb)]);
disp(['货损成本：',num2str(hscb)]);
disp(['时间惩罚成本：',num2str(cfcb)]);
%% 判断最优解是否满足时间窗约束和载重量约束，0表示违反约束，1表示满足全部约束
flag=Judge(bestVC,cap,demands,a,b,L,s,dist,chesu,bl);
%% 检查最优解中是否存在元素丢失的情况，丢失元素，如果没有则为空
DEL=Judge_Del(bestVC,cusnum);
init_v=vehicle_load(bestVC,demands);
%% 画出最终路线图
draw_Best(bestVC,zuobiao);
% save c101.mat
% toc

结果

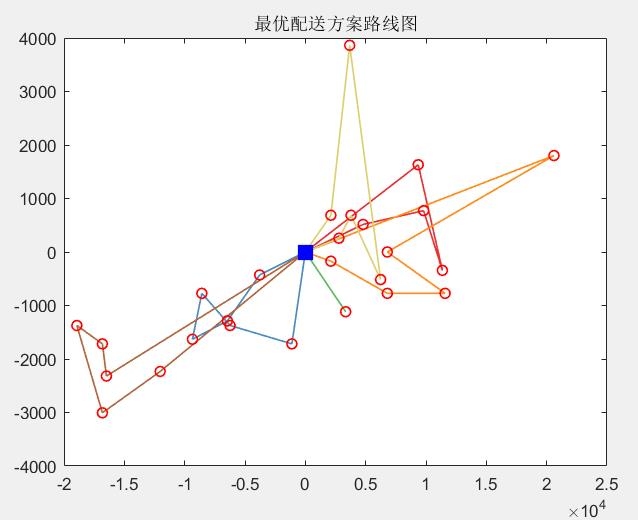
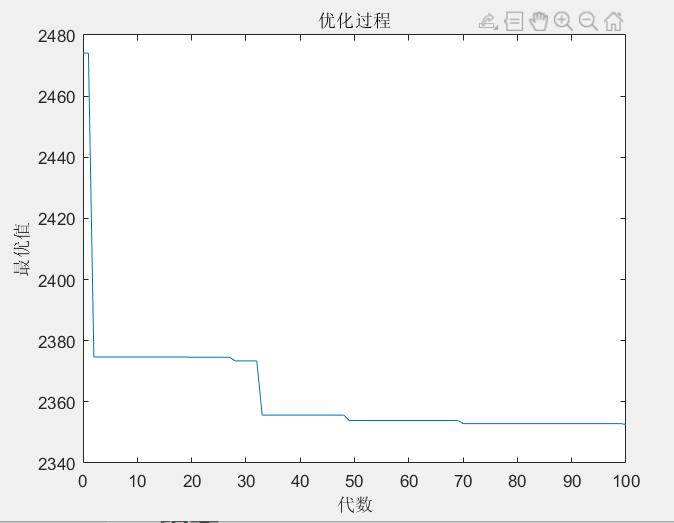
最优解:
车辆使用数目：6，车辆行驶总距离：159.1788

总成本：2352.5824
固定成本：1110
变动成本：318.3575
制冷成本：36.8716
货损成本：103.9378
时间惩罚成本：783.4155
配送路线1：0->13->6->15->12->0
配送路线2：0->16->17->19->18->20->21->0
配送路线3：0->1->0
配送路线4：0->14->7->8->9->10->0
配送路线5：0->11->2->5->3->4->0
配送路线6：0->22->24->25->26->23->0

如需代码或代写vx:zzs1056600403