重链剖分求LCA

Posted 2021-05-17 PushyTao

洛谷P3379

• • 题目描述
  • 输入格式
  • 输出格式
  • 输入输出

题目链接
倍增做法求LCA 在 这篇博客中有提到

题目描述

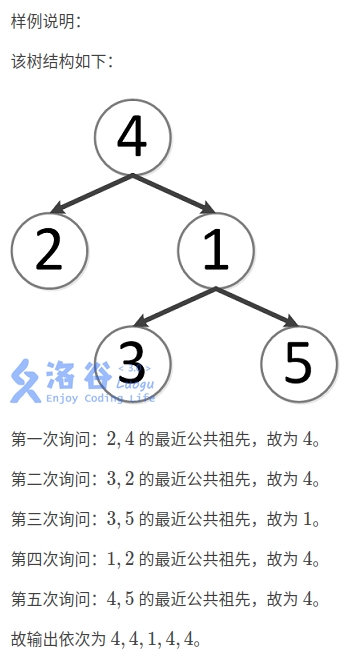
如题，给定一棵有根多叉树，请求出指定两个点直接最近的公共祖先。

输入格式

第一行包含三个正整数 N,M,SN,M,S，分别表示树的结点个数、询问的个数和树根结点的序号。
接下来 N-1N−1 行每行包含两个正整数 x, yx,y，表示 xx 结点和 yy 结点之间有一条直接连接的边（数据保证可以构成树）。
接下来 MM 行每行包含两个正整数 a, ba,b，表示询问 aa 结点和 bb 结点的最近公共祖先。

输出格式

输出包含 MM 行，每行包含一个正整数，依次为每一个询问的结果。

输入输出

样例 1
输入

5 5 4
3 1
2 4
5 1
1 4
2 4
3 2
3 5
1 2
4 5

输出

4
4
1
4
4

说明/提示
对于 30% 的数据，N≤10，M≤10。

对于 70% 的数据，N≤10000，M≤10000。

对于 100% 的数据，N≤500000，M≤500000。

int lca(int u,int v) {
	while(top[u] != top[v]) {
		if(dep[top[u]] < dep[top[v]]) swap(u,v);
		u = fa[top[u]];
	}
	if(dep[u] < dep[v]) return u;
	else return v;
}

对于要求树上两个点u,v的lca，（当两个点不在一条重链上的时候）我们可以每次先让链头深depth比较大的点进行移动，不在一条重链上直接将top更深的节点跳到链头的父节点u = fa[top[u]]; ，当两个点在一条重链上的时候，从深度的角度来看，深度比较小的就应该是祖先节点

int n,m,rt;
struct node {
	int to;
	int nex;
} e[maxn];
int head[maxn],cnt;
void init() {
	for(int i=0; i<maxn; i++) head[i] = -1;
	cnt = 0;
}
void add(int u,int v) {
	e[cnt].to = v;
	e[cnt].nex = head[u];
	head[u] = cnt ++;
}
int fa[maxn],siz[maxn],son[maxn],dep[maxn],top[maxn];
void dfs1(int x) {
	siz[x] = 1;
	dep[x] = dep[fa[x]] + 1;
	for(int i=head[x]; ~i; i=e[i].nex) {
		int to = e[i].to;
		// fa[to] = x;
		if(to != fa[x]) {
			fa[to] = x;
			dfs1(to);
			siz[x] += siz[to];
			if(siz[to] > siz[son[x]]) son[x] = to;
		}
	}
}
void dfs2(int rt,int tp) {
	top[rt] = tp;
	if(son[rt]) dfs2(son[rt],tp);
	for(int i = head[rt]; ~i; i = e[i].nex) {
		int to = e[i].to;
		if(to != fa[rt] && to != son[rt]) dfs2(to,to);
	}
}
int lca(int u,int v) {
	while(top[u] != top[v]) {
		if(dep[top[u]] < dep[top[v]]) swap(u,v);
		u = fa[top[u]];
	}
	if(dep[u] < dep[v]) return u;
	else return v;
}
int main() {
	cin >> n >> m >> rt;
	init();
	for(int i = 1; i < n; i++) {
		int u=read,v=read;
		add(u,v);
		add(v,u);
	}
	dfs1(rt);
	dfs2(rt,rt);
	while(m --) {
		int u=read,v=read;
		cout<<lca(u,v)<<endl;
	}
	return 0;
}