RSA公钥体系 与在 ssh中免密的登陆的应用

Posted 2021-05-17 _luckylight

一、秘钥体系

    第一部分查看书籍为 北京大学出版社出版的 丘维声老师的 数学思维方式与创新
    在之前安全协议的讲解中，很多的协议都是用了秘钥的这一概念，相信很多同学对这不求甚解，下面我来系统的介绍秘钥体系，并且证明一下如今的公钥私钥RSA密码系统。
秘钥，即密钥，在密码学中，密钥（key，又常称金钥）是指某个用来完成加密、解密、完整性验证等密码学应用的秘密信息。在对称密码学（或称密钥密码学）中，加密和解密用的是同一个钥匙，因此钥匙需要保密。而在公钥密码学（或称非对称密码学）中，加密和解密用的钥匙不同：通常一个是公开的，称为公钥；另一个保密，称为私钥。

1.1 传统加密

    传统的加密方法是加密、解密使用同样的密钥，由发送者和接收者分别保存，在加密和解密时使用。但这带来一个问题是密钥的生成、注入、存储、管理、分发等很复杂，特别是随着用户的增加，密钥的需求量成倍增加。

1.2 RSA密码系统(重点)

    1976年美国斯坦福大学的两名学者迪菲和赫尔曼提出了公开密钥密码体制的概念。所谓的公开密钥密码体制就是使用不同的加密密钥与解密密钥，是一种“由已知加密密钥推导出解密密钥在计算上是不可行的”密码体制。
    为了论述清楚计算上不可行的问题，我们给出一下定理：

1.3 欧拉函数

    在数论，对正整数n，欧拉函数是小于或等于n的正整数中与n互质的数的数目（因此φ(1)=1）。
下面我们给出欧拉函数的计算公式：
$\phi (n)=n(1-\frac{1}{p_1})(1-\frac{1}{p_2})\dots (1-\frac{1}{p_k}),n=p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}\cdots p_n^{{\alpha }_n}$
其中p1, p2……pn为x的所有质因数，x是不为0的整数
那么是如何证明的呢？下面我给出一个比较简单的证明方法(容斥定理)

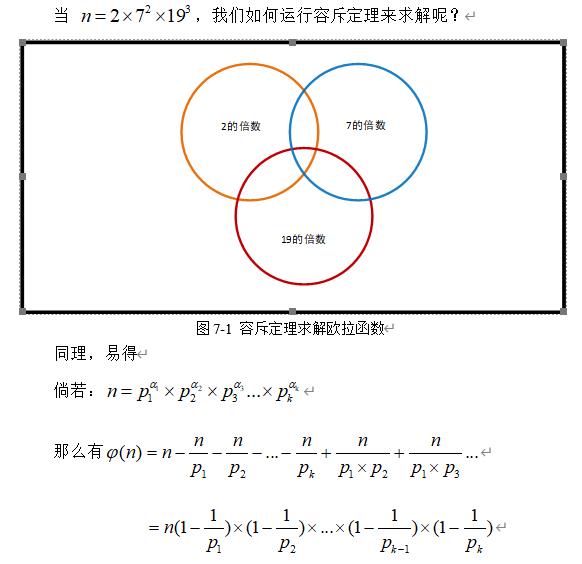
1.4 欧拉定理

    在数论中，欧拉定理,（也称费马-欧拉定理）是一个关于同余的性质。欧拉定理表明，若n,a为正整数，且n, a互质，则:

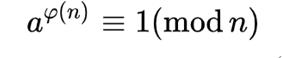
1.5 公钥私钥体系的引入

知道这两个定理之后，让我们联想一下加密的过程：
发送方A需要向接收方B发送报文，首先在发送方 A 通过 a 的幂进行加密，将加密后的内容发送给B，然后 接收方B 通过 b 的幂进行还原。而且对于取模的幂运算可以通过快速幂算法在 log(a) 的复杂度下完成，过程如下图7-2所示

下面我们给出一个公钥私钥的方案，查看他是否可行：
接收方 B，自己设计出 a, b, n，其中 a, b, n满足的关系为$ab\equiv k\phi (n)+1$ ，接收方 B，将其中的 作为公钥，公布在互联网上，将 b 作为私钥，内部保留，那么上述的过程就可以得以实现，即该算法是可行的。


    下面，我们来考虑一下，这种机制是否安全，当攻击者 接收到 ${\overline{x}}^a$，能否通过公布在互联网上的公钥 $(a,n)$，计算出 $b$，进而解密，获取发送方A的原内容 即 ？
    在公式 $ab\equiv k\phi (n)+1$中，已知 ，倘若攻击者知道$a$和$\phi (n)$ ，就可以使用扩展的欧几里得算法，可以在 $log(n)$的复杂度内，找到未知数 b, k 的一组解决方案，完成密码破解。

1.6 欧几里得算法与扩展欧几里得算法

    这里，我简单介绍一下欧几里得算法和扩展欧几里得算法

欧几里得算法

    首先，我们将a, b的最大公约数greatest common divisor，记作gcd(a, b)
    欧几里得算法就是为了求出两个数a、b的最大公约数，他利用gcd(a, b) == gcd(b, a%b)，将问题不多进行递归求解，使用 c 语言书写的代码如下（本人手写）

int gcd(int a, int b){
    if(b == 0)  return a;
    else    return gcd(b, a % b);
}

扩展的欧几里得算法

  是对于欧几里得算法的扩展，在原本求解gcd(a, b)的基础之上，求解 的问题。
对应的c++代码如下，证明过程即为代码的第一段注释（本人手写）：

/*
exgcd(a, b, x, y):
    a * x + b * y == gcd(a, b);
exgcd(b, a % b, y, x):
    b * y + (a - a / b * b) * x == gcd (b, a % b)
    a * x + b * (y - a / b * x) == gcd (a, b)


所以说可得递归通式:
    gcd(a, b, x, y):
        gcd(b, a % b, y, x)求结果
        y -= a / b * x;
递归终点:
    b == 0 时, a * x + 0 * y == a
        x = 1, y = 0
    
*/
LL exgcd(LL a, LL b, LL &x, LL &y) {
    if (b == 0LL) {
        x = 1, y = 0;
        return a;
    } else {
        exgcd(b, a % b, y, x);
        y -= a / b * x;
    }
}

1.7 公钥私钥的具体实现

    通过刚刚的扩展的欧几里得算法，可以在破解者在已知 $(a,\phi (n))$的前提下，可以在$O(log(N)$ 的时间复杂度下求出 中的$b$, 破解出私钥，但是知道破解者知道 $n$，就可以求出 $\phi (n)$吗？之前已经证明过欧拉函数的公式，如下所示:

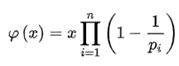
  下面对 $\\varphi (n) $的求解，转移为了将 n 进行质数分解，分解成以下形式：

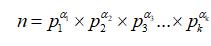
  那么，该分解的复杂度为多少了？复杂度为$O(\sqrt{n})$ ，当我们n很大时，比如 $10^{60}$，此时普通计算机的求解就需要100年。
但是，攻击者无法求解出 $\phi n$，接收方B是如何求解 的呢？原来，接收方仅仅只需要选取两个大的质数，p, q，然后让 $n=pq$，因此可得 $\phi (n)=(p-1)(q-1)$，求解完毕。
    至此，公开密钥密码体制基本概念讲解完毕！

二、ssh密钥登录原理与实现免密登陆

第二部分参考博客

公钥和私钥都属于非对称加密算法的一个实现，这个加密算法的信息交换过程是：(乙向甲请求远程登录)

1. 持有公钥的一方（甲）在收到持有私钥的一方（乙）的请求时，甲会在自己的公钥列表中查找是否有乙的公钥，如果有则使用一个随机字串使用公钥加密并发送给乙。
2. 乙收到加密的字串使用自己的私钥进行解密，并将解密后的字串发送给甲。
3. 甲接收到乙发送来的字串与自己的字串进行对比，如过通过则验证通过，否则验证失败。

也就是说，请求登陆他人计算机的 客户机 需要有自己的公钥和私钥，并将自身公钥发送给 被登录机 （服务机）

    非对称加密算法不能使用相同的密钥进行解密，也就是说公钥加密的只能使用私钥进行解密。
这一部分可以通过第一部分的证明得知 $ab\equiv k\phi (n)+1$，仅仅使用 $a$，或者是 仅仅使用 $b$ 是没有这个等式关系的

2.1 免密登陆过程

ssh使用私钥登录大致步骤就是：主机A（客户端）创建公钥私钥，并将公钥复制到主机B（被登陆机）的指定用户下，然后主机A使用保存私钥的用户登录到主机B对应保存公钥的用户。

(1) 实验环境
两台主机：

1. 主机A（客户机）：192.168.187.137
2. 主机B（被登陆机）：192.168.187.142

(2) 实验开始
在需要免密登陆的主机（主机A）下生成公钥和私钥

ssh-keygen -t rsa     ##-t rsa可以省略，默认就是生成rsa类型的密钥

说明：命令执行后会有提示，输入三次回车即可，执行完成后会在当前用户的.ssh目录下生成两个文件：id_rsa、id_rsa.pub文件，前者时私钥文件，后者是公钥文件（拷贝到其他主机只需要拷贝这个文件的内容）

将公钥复制到被登陆的主机上的 ~/.ssh/authorized_keys 文件中
拷贝公钥有两种方法，其原理都相同：


方式一：使用 ssh-copy-id 直接拷贝
使用 ssh-copy-id 进行拷贝公钥非常方便，只需要指定目标主机和目标主机的用户即可。

ssh-copy-id -i ~/.ssh/id_rsa.pub root@192.168.187.142

执行这条命令后会自动将登录主机的公钥文件内容追加至目标主机中指定用户（root）.ssh目录下的authorized_keys文件中。这个过程是全自动的，非常方便。


方法二：自己创建文件进行拷贝

1. 在登录主机（客户机）上创建authorized_keys文件并将公钥追加到该文件。

cat id_rsa.pub >> authorized_keys
chmod 600 authorized_keys     ##修改文件权限为600，该文件有规定如果属组其他人出现可写则文件就不会生效

2. 在被登录机的指定用户家目录下创建 .ssh 目录（这里在root用户下创建，因为要使用密钥登陆到root用户），你也可以使 hadoop 用户

mkdir .ssh
chmod 700 .ssh     ##将目录权限改为700该目录的权限必须是700才有效

3. 将登录机创建的authorized_keys文件拷贝到被登录机，使用scp

scp authorized_keys root@192.168.187.142:/root/.ssh/
authorized_keys                                  100%  402   576.4KB/s   00:00

2.2 免密登陆

登录
使用主机A乙root用户身份登陆到主机B

ssh root@192.168.187.142
Last login: Wed Feb 13 15:24:30 2019 from 192.168.187.137

    首次登录将弹出保存信息，输入yes即可，此时已经实现了免密的密钥登陆。
注意事项和说明
    上例只能实现主机A免密登陆到主机B的root用户，如果想让主机B也免密登录到主机A，创建密钥和拷贝步骤相同。
    密钥登陆的方式只能登录被登录机中 .ssh 目录下有对应公钥的用户，如果想让所有用户都可以被登录则需要将authorized_keys文件的内容追加到其他用户的 ~/.ssh/authorized_keys 文件中。
    如果使用自己创建的authorized_keys文件进行复制公钥则要严格设置权限，权限不正确会导致文件无法使用，也就无法进行密钥验证。

再次说明，第二部分参考至博客园的一个博客