动态规划之最长上升子序列模型
Posted _luckylight
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了动态规划之最长上升子序列模型相关的知识,希望对你有一定的参考价值。
动态规划分为很多模型,比如说数字三角形模型,最长上升子序列模型,背包模型,状态机模型,状态压缩,区间dp,树形dp等等
下面,我就Acwing提高课中,最长上升子序列模型进行了整理。
涉及知识点总览
主要涉及的算法知识点有:
- 最长上升子序列 O ( N 2 ) O(N^2) O(N2)和 O ( N l o g N ) O(NlogN) O(NlogN)求解方法
- 正反双向 LIS
- 最大上升子序列和
- 偏序集-Dilworth定理的两种证明
这里补充一个
O
(
N
2
)
O(N^2)
O(N2) dp 数组的优化
f[i] 代表的是 以 i 为结尾的最长上升子序列的长度,他需要 f[i-1] …f[i-2] … 的信息来更新自己
参考网上思路,发现可以用树状数组。用数值做下标,维护长度最大值,从后往前循环,每次查询之前已经放到树状数组里面的数中以这个数结尾的最长不上升子序列的长度的最大值,然后把这个最大值+1作为以自己结尾的最长不上升子序列的长度,放到树状数组里面
这里我们简单温习一下树状数组:
一、怪盗基德的滑翔翼
题目链接如下 怪盗基德的滑翔翼

根据题目的描述信息可知,该题目就是要求对于某一个建筑,往 左 能够最长下降子序列的长度,或者是往 右的租场下降子序列的长度,因此有两种解法一种是我们常见的dp最长上升子序列,还有一种就是贪心最长上升子序列。
下面,是我给出的两种解法,具体的解释都放在了代码里面
#include <bits/stdc++.h>
using namespace std;
const int N = 110;
int f[N], a[N], g[N];
int ans, n;
/*
dp LIS
f[i] = f[j] + 1 (j < i && a[j] < a[i])
正方跑两次
*/
void sol1() {
int ans = 0;
for (int i = 1; i <= n; i ++ ) {
f[i] = 1;
for (int j = 1; j < i; j ++ ) {
if (a[j] < a[i]) {
f[i] = max(f[i], f[j] + 1);
}
}
ans = max(ans, f[i]);
}
for (int i = n; i >= 1; i -- ) {
g[i] = 1;
for (int j = n; j > i; j -- ) {
if (a[j] < a[i]) {
g[i] = max(g[i], g[j] + 1);
}
}
ans = max(ans, g[i]);
}
printf("%d\\n", ans);
}
/*
使用最长上升子序列模型的贪心解法
f[i] 表示长度为 i 的最小末尾
不难得知,f[i] 数组应该是单调递增的(相等的情况都不会出现)
对于每次循环 数组 a 的元素,都是将 寻找小于 a[i] 的最大 f[j] 的位置,然后更新f[j + 1]
初始化数组memset(f, 0x3f, sizeof f), f[0] = 0;
*/
void sol2() {
int len = 1, ans = 0;
memset(f, 0x3f, sizeof f);
f[0] = 0;
f[1] = a[1];
for (int i = 2; i <= n; i ++ ) {
static int l, r, mid;
l = 0, r = len;
while (l < r) {
mid = l + r + 1 >> 1; // 注意这里的 + 1
if (f[mid] < a[i]) {
l = mid;
} else {
r = mid - 1;
}
}
f[l + 1] = a[i];
len = max(len, l + 1); // 更新 len
}
ans = max(ans, len);
len = 1;
memset(f, 0x3f, sizeof f);
f[0] = 0;
f[1] = a[n];
for (int i = n - 1; i >= 1; i -- ) {
static int l, r, mid;
l = 0, r = len;
while (l < r) {
mid = l + r + 1 >> 1; // 注意这里的 + 1
if (f[mid] < a[i]) {
l = mid;
} else {
r = mid - 1;
}
}
f[l + 1] = a[i];
len = max(len, l + 1);
}
ans = max(ans, len);
printf("%d\\n", ans);
}
int main()
{
int T; cin >> T;
while (T -- ) {
scanf("%d", &n);
for (int i = 1; i <= n; i ++ ) {
scanf("%d", &a[i]);
}
// sol1();
sol2();
}
return 0;
}
二、登山
Acwing 登山题目链接
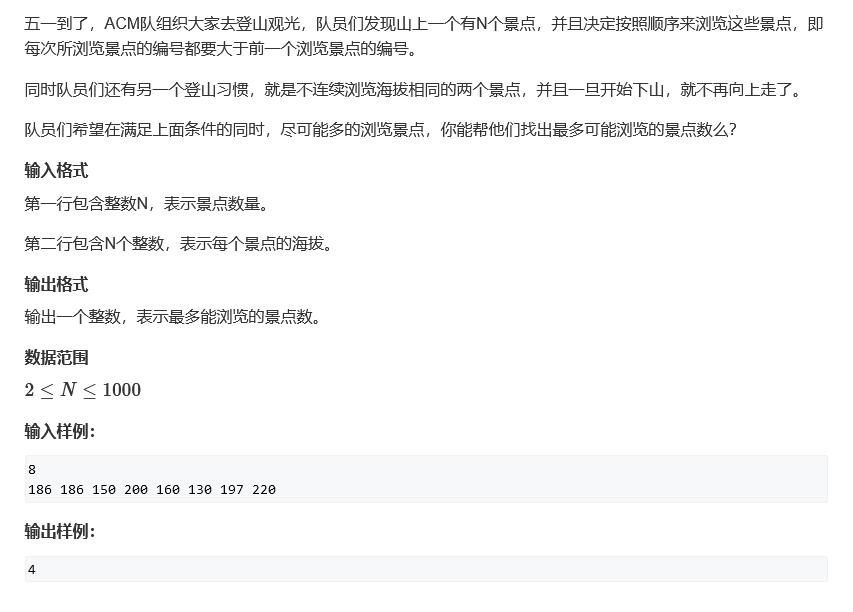
该登山题目和原本的 怪盗基德 问题有些类似,但是又有些不同,他们都需要正反两次求出最长上升子序列,但是不同的是怪盗基德可以使用 nlog(n) 的贪心算法,因为他不必在意于最后的结尾是哪个点。
但是,登山问题是需要知道 该点的位置是在哪里的。
因此登山问题必须要使用
O
(
N
2
)
O(N^2)
O(N2)的dp求解,
f[i] 表示以i 为结尾的最长上升子序列
#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
int f[N], a[N], g[N];
int ans, n;
/*
dp LIS
f[i] = f[j] + 1 (j < i && a[j] < a[i])
正方跑两次
*/
void sol1() {
int ans = 0;
for (int i = 1; i <= n; i ++ ) {
f[i] = 1;
for (int j = 1; j < i; j ++ ) {
if (a[j] < a[i]) {
f[i] = max(f[i], f[j] + 1);
}
}
}
for (int i = n; i >= 1; i -- ) {
g[i] = 1;
for (int j = n; j > i; j -- ) {
if (a[j] < a[i]) {
g[i] = max(g[i], g[j] + 1);
}
}
}
for (int i = 1; i <= n; i ++ ) {
ans = max(ans, f[i] + g[i] - 1); // 注意这里的 - 1
}
printf("%d\\n", ans);
}
int main()
{
int T; T = 1;
while (T -- ) {
scanf("%d", &n);
for (int i = 1; i <= n; i ++ ) {
scanf("%d", &a[i]);
}
sol1();
}
return 0;
}
三、合唱队形
Acwing 合唱队型

本题就是换了一种问法,最少有多少同学出列,就是需要求出我们的最长上升子序列,和我们的登山问题是一个性质,也是只可以使用
O
(
N
2
)
O(N^2)
O(N2)算法进行求解
#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
int f[N], a[N], g[N];
int ans, n;
/*
dp LIS
f[i] = f[j] + 1 (j < i && a[j] < a[i])
正方跑两次
*/
void sol1() {
int ans = 0;
for (int i = 1; i <= n; i ++ ) {
f[i] = 1;
for (int j = 1; j < i; j ++ ) {
if (a[j] < a[i]) {
f[i] = max(f[i], f[j] + 1);
}
}
}
for (int i = n; i >= 1; i -- ) {
g[i] = 1;
for (int j = n; j > i; j -- ) {
if (a[j] < a[i]) {
g[i] = max(g[i], g[j] + 1);
}
}
}
for (int i = 1; i <= n; i ++ ) {
ans = max(ans, f[i] + g[i] - 1); // 注意这里的 - 1
}
printf("%d\\n", n - ans);
}
int main()
{
int T; T = 1;
while (T -- ) {
scanf("%d", &n);
for (int i = 1; i <= n; i ++ ) {
scanf("%d", &a[i]);
}
sol1();
}
return 0;
}
四、友好城市
Acwing 友好城市链接

对于本题而言,他所求的不相交的航线,就是我们排序之后的不递减子序列!
排序,可以按照是左岸排序,也可以按照右岸进行排序
/*
这个题目个关键在于,你连一连这个友好城市的航线,你就会发现
航线不相交,就是排序之后他们的那个最长上升子序列
*/
#include <bits/stdc++.h>
using namespace std;
const int N = 5010;
int n, f[N], len;
class Node {
public:
int x, y;
Node() {
//
}
Node(int x, int y): x(x), y(y) {
//
}
}a[N];
bool cmp1(const Node &t1, const Node &t2) {
if (t1.x == t2.x) {
return t1.y <= t2.y;
} else {
return t1.x < t2.x;
}
}
bool cmp2(const Node &t1, const Node &t2) {
if (t1.y == t2.y) {
return t1.x <= t2.x;
} else {
return t1.y < t2.y;
}
}
int sol1() {
sort(a + 1, a + n + 1, cmp1);
// sort(a + 1, a + n + 1, cmp2);
// 求解的是最长非递减子序列
/*
因此变成了寻找 f[i] 中 小于等于 val 的最大位置
*/
int val;
memset(f, 0x3f, sizeof f);
f[0] = 0;
len = 0;
for (int i = 1; i <= n; i ++ ) {
val = a[i].y;
static int l, r, mid;
l = 0, r = len;
while (l < r) {
mid = l + r + 1 >> 1;
if (f[mid] <= val) { // 注意这里是 小于等于
l = mid;
} else {
r = mid - 1;
}
}
f[l + 1] = val;
len = max(len, l + 1);
}
cout << len << endl;
}
int sol2() {
sort(a + 1, a + n + 1, cmp2);
// 求解的是最长非递减子序列
/*
因此变成了寻找 f[i] 中 小于等于 val 的最大位置
*/
int val;
memset(f, 0x3f, sizeof f);
f[0] = 0;
len = 0;
for (int i = 1; i <= n; i ++ ) {
val = a[i].x;
static int l, r, mid;
l = 0, r = len;
while (l < r) {
mid = l + r + 1 >> 1;
if (f[mid] <= val) { // 注意这里是 小于等于
l = mid;
} else {
r = mid - 1;
}
}
f[l + 1] = val;
len = max(len, l + 1);
}
cout << len << endl;
}
int main()
{
cin >> n;
for (int i = 1; i <= n; i ++ ) {
scanf("%d%d", &a[i].x, &a[i].y);
}
//sol1();
sol2();
return 0;
}
五、最大上升子序列和
Acwing 最大上升子序列和链接
 以上是关于动态规划之最长上升子序列模型的主要内容,如果未能解决你的问题,请参考以下文章
以上是关于动态规划之最长上升子序列模型的主要内容,如果未能解决你的问题,请参考以下文章