python深度学习进阶-自然语言处理-自然语言和单词的分布式表示
Posted 诗雨时
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了python深度学习进阶-自然语言处理-自然语言和单词的分布式表示相关的知识,希望对你有一定的参考价值。
深度学习进阶-自然语言处理-自然语言和单词的分布式表示
摘要
- 使用 WordNet 等同义词词典,可以获取近义词或测量单词间的相似度等。
- 使用同义词词典的方法存在创建词库需要大量人力、新词难更新等问题。
- 目前,使用语料库对单词进行向量化是主流方法。
- 近年来的单词向量化方法大多基于 “单词含义由其周围的单词构成” 这一分布式假设。
- 在基于计数的方法中,对语料库中的每个单词周围的单词的出现频数进行计数并汇总(=共现矩阵)。
- 通过将共现矩阵转化为 PPMI 矩阵并降维,可以将大的稀疏向量转变为小的密集向量。
- 在单词的向量空间中,含义上接近的单词距离上理应也更近。
1. 什么是自然语言处理
自然语言(natural language):我们平常使用的语言,如汉语或英语,称为自然语言(natural language)。
自然语言处理(Natural Language Processing,NLP):顾名思义,就是处理自然语言的科学。简单地说,它是一种能够让计算机理解人类语言的技术。换言之,自然与处理的目标就是让计算机理解人说的话,进而完成对我们有帮助的事情。
我们的语言是由文字构成的,而语言的含义是由单词构成的。换句话说,单词是含义的最小单位。
2. 同义词词典
同义词词典(thesaurus):具有相同含义的单词(同义词)或含义类似的单词(近义词)被归类到同一个组中。比如,使用同义词词典,我们可以知道 car 的同义词有 automobile、motorcar等(图 2-1)。
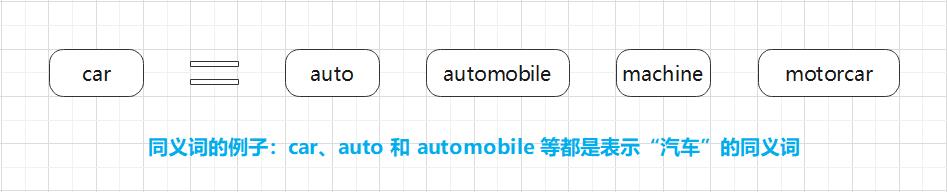
在自然语言处理中用到的同义词词典有时会定义比单词之间的粒度更细的关系,比如 “上位-下位” 关系、“整体-部分” 关系。举个例子,如图 2-2 所示,我们利用图结构定义了各个单词之间的关系。
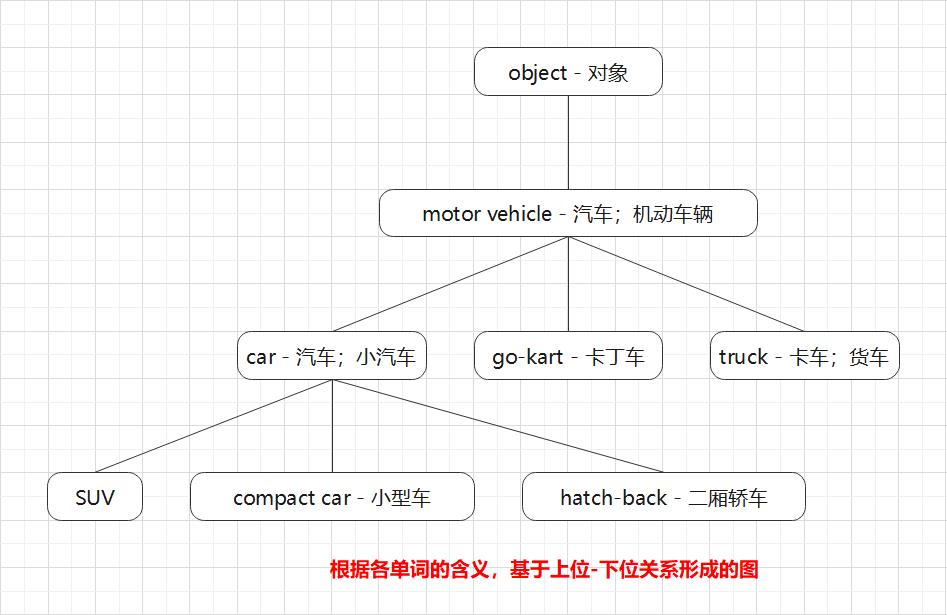
在图 2-2 中,单词 motor vehicle(机动车)是单词 car 的上位概念。car 的下位概念有 SUV、compact car 和 hatch-back 等更加具体的车种。
像这样,通过对所有单词创建近义词集合,并用图表示各个单词的关系,可以定义单词之间的联系。利用这个 “单词网络”,可以教会计算机单词之间的相关性。也就是说,我们可以将单词含义(间接地)教给计算机,然后利用这一知识,就能让计算机做一些对我们有用的事情。
如何使用同义词词典根据自然语言处理的具体应用的不同而不同。比如,在信息检索场景中,如果事先知道 automobile 和 car 是近义词,就可以将 automobile 的检索结果添加到 car 的检索结果中。
2.1 WordNet
WordNet:自然语言处理领域最著名的同义词词典。由普林斯顿大学于 1985 年开始开发的同义词词典。
使用 WordNet,可以获得单词的近义词,或者利用单词网络。使用单词网络,可以计算单词之间的相似度。
2.2 同义词词典的问题
难以顺应时代变化
我们使用的语言是活的。随着时间的推移,新词不断出现,而那些落满尘埃的旧词不知哪天就会被遗忘。比如,“众筹”(crowdfunding)就是一个最近才开始使用的新词。
另外,语言的含义也会随着时间的推移而变化。比如,英语中的 heavy 一词,现在有 “事态严重” 的含义(主要用于俚语),但以前是没有这种用法的。在电影《回到未来》中,有这样一个场景:从 1985 年穿越回来的马蒂和生活在 1955 年的博士的对话中,对 heavy 的含义有不同的理解。如果要处理这样的单词变化,就需要人工不停地更新同义词词典。
人力成本高
制作词典需要巨大的人力成本。以英文为例,据说现有的英文单词总数超过 1000 万个。在极端情况下,还需要对如此大规模的单词进行单词之间的关联。
顺便提一下,WordNet 中收录了超过 20 万个的单词。
无法表示单词的微妙关系
同义词词典中将含义相近的词分到一组。但实际上,即使含义相近的单词,也有细微的差别。比如,wintage(复古) 和 retro(复古)虽然表示相同的含义,但是用法不同,而这种细微的差别在同义词词典中是无法表示出来的。
3. 基于计数的方法
语料库(corpus):大量的文本数据。语料库中包含了大量的关于自然语言的实践知识,即文章的写作方法、单词的选择方法和单词含义等。
3.1 基于 Python 的语料库的预处理
import re
import numpy as np
def preprocess(text):
"""
文本语料预处理
:param text: 需要进行预处理的文本内容
:return:
"""
text = text.lower() # 将所有字母转化为小写
# 方案一
words = re.split("\\W+", text) # \\W 匹配任何非单词字符。等价于 "[^A-Za-z0-9_]"
# 方案二
# text = text.replace(".", " .") # 句尾的句号前插入一个空格
# words = text.split(" ") # 通过空格分割句子
word_to_id = {} # 将单词转化为单词ID(健是单词,值是单词ID)
id_to_word = {} # 将单词ID转化为单词(健是单词ID,值是单词)
for word in words:
if word not in word_to_id:
new_id = len(word_to_id)
word_to_id[word] = new_id
id_to_word[new_id] = word
# 单词列表转化为单词ID列表
corpus = np.array([word_to_id[w] for w in words])
return corpus, word_to_id, id_to_word
if __name__ == "__main__":
text = "You say goodbye and I say hello."
corpus, word_to_id, id_to_word = preprocess(text)
print(corpus)
print(word_to_id)
print(id_to_word)[0 1 2 3 4 1 5 6]
{'you': 0, 'say': 1, 'goodbye': 2, 'and': 3, 'i': 4, 'hello': 5, '': 6}
{0: 'you', 1: 'say', 2: 'goodbye', 3: 'and', 4: 'i', 5: 'hello', 6: ''}3.2 单词的分布式表示
单词的分布式表示:将单词表示为固定长度的向量。
这种向量的特征在于它是用密集向量表示的。密集向量的意思是,向量的各个元素(大多数)是由非 0 实数表示的。例如,三维分布表示是 [0.21, -0.45, 0.83]。
3.3 分布式假设
分布式假设(distributional hypothesis):某个单词的含义由它周围的单词形成。
单词本身没有含义,单词含义由它所在的上下文(语境)形成。的确,含义相同的单词经常出现在相同的语境中。比如 “I drink beer.” “I drink wine.”,drink 的附近常有饮料出现。另外,从 “I guzzle beer.” “I guzzle wine.” 可知,guzzle(大口喝) 和 drink(喝) 所在的语境相同。进而我们可以推测出,guzzle 和 drink 是近义词。
上下文:某个居中单词(关注词)周围的单词(词汇)。在图 2-3 的例子中,左侧和右侧的 2 个单词就是上下文。

将左右两边相同数量的单词作为上下文。但是,根据具体情况,也可以仅将左边的单词或者右边的单词作为上下文。此外,也可以使用考虑了句子分隔符的上下文。
窗口大小(window size):将上下文的大小(即周围的单词有多少个)称为窗口大小(window size)。
窗口大小为 1,上下文包含左右各 1个单词;窗口大小为 2,上下文包含左右各 2 个单词,以此类推。
3.4 共现矩阵
基于计数的方法:在关注某个单词的情况下,对它的周围出现了多少次什么单词进行计数,然后汇总。
计算 “you say goodbye and i say hello.” 中各个单词的上下文中包含的单词的频数:
设置窗口大小为 1,从单词 ID 为 0 的 you 开始。
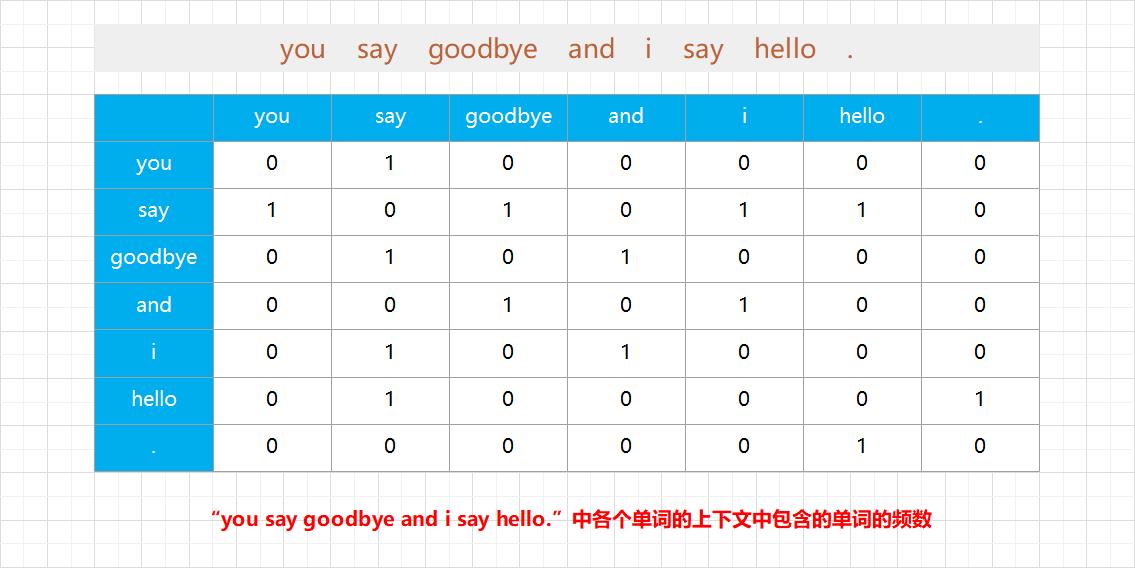
图 2-4 是汇总了所有单词的共现单词的表格。这个表格的各行对应相应单词的向量。因为图 2-4 的表格呈矩阵状,所以称为共现矩阵(co-occurence matrix)。
def create_co_matrix(corpus, vocab_size, window_size=1):
"""
生成共现矩阵
:param corpus: 语料库(单词ID列表)
:param vocab_size: 词汇个数
:param window_size: 窗口大小(当窗口大小为1时,左右各1个单词为上下文)
:return: 共现矩阵
"""
corpus_size = len(corpus)
co_matrix = np.zeros((vocab_size, vocab_size), dtype=np.int32)
for idx, word_id in enumerate(corpus):
for i in range(1, window_size + 1):
left_idx = idx - i
right_idx = idx + i
if left_idx >= 0:
left_word_id = corpus[left_idx]
co_matrix[word_id, left_word_id] += 1
if right_idx < corpus_size:
right_word_id = corpus[right_idx]
co_matrix[word_id, right_word_id] += 1
return co_matrix3.5 向量间的相似度
测量单词的向量表示的相似度的方法:余弦相似度(cosine similarity)。设有 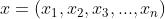 和
和 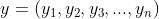 两个向量,它们之间的余弦相似度的定义方式如下式所示。
两个向量,它们之间的余弦相似度的定义方式如下式所示。
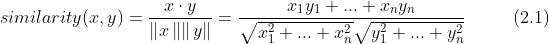
式 (2.1) 中,分子是向量内积,分母是各个向量的范数。范数表示向量的大小,这里计算的是 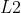 范数(即向量各个元素的平方和的平方根)。式 (2.1) 的要点是先对向量进行正规化,再求它们的内积。
范数(即向量各个元素的平方和的平方根)。式 (2.1) 的要点是先对向量进行正规化,再求它们的内积。
余弦相似度直观地表示了 “两个向量在多大程度上指向同一方向”。两个向量完全指向相同的方向时,余弦相似度为 1;完全指向相反的方向时,余弦相似度为 -1。
Python 实现余弦相似度计算:
def cos_similarity(x, y, eps=1e-8):
"""
计算余弦相似度
:param x: 向量
:param y: 向量
:param eps: 用于防止“除数为0”的微小值
:return:
"""
nx = x / (np.sqrt(np.sum(x)) + eps) # x的正规化
ny = y / (np.sqrt(np.sum(y)) + eps) # y的正规化
return np.dot(nx, ny) # 计算两个向量的内积实验:求句子 "You say goodbye and I say hello." 中单词 "You" 和单词 "I" 的相似度。
"""余弦相似度"""
import sys
sys.path.append("..")
from common.util import preprocess, create_co_matrix, cos_similarity
text = "You say goodbye and I say hello." # 文本
corpus, word_to_id, id_to_word = preprocess(text) # 文本语料预处理
vocab_size = len(word_to_id) # 词汇大小
matrix = create_co_matrix(corpus, vocab_size) # 生成共现矩阵
vector_you = matrix[word_to_id["you"]] # you的单词向量
vector_i = matrix[word_to_id["i"]] # i的单词向量
con_simi = cos_similarity(vector_you, vector_i) # 计算余弦相似度
print(con_simi)
# 0.7071067691154799从上面的结果可知,"you" 和 "i" 的余弦相似度是 0.7071067691154799。由于余弦相似度的取值范围是 -1 到 1,所以可以说这个值是相对较高的(存下相似性)。
3.6 相似单词的排序
实验:当某个单词被作为查询词时,将与这个查询词相似的单词按降序显示出来。
def most_similarity(query, word_to_id, id_to_word, word_matrix, top=5):
"""
相似单词的查找
:param query: 查询词
:param word_to_id: 从单词到单词ID的字典
:param id_to_word: 从单词ID到单词的字典
:param word_matrix: 汇总了单词向量的矩阵,假定保存了与各行对应的单词向量
:param top: 显示到前几位
:return:
"""
# 1. 取出查询词的单词向量
if query not in word_to_id:
print(f"{query} is not found")
return
print(f"\\n[query]{query}")
query_id = word_to_id[query]
query_vector = word_matrix[query_id]
# 2. 分别求得查询词的单词向量和其他所有单词向量的余弦相似度
vocab_size = len(word_to_id) # 词汇大小
similarity = np.zeros(vocab_size)
for i in range(vocab_size):
similarity[i] = cos_similarity(word_matrix[i], query_vector)
# 3. 基于余弦相似度的结果,按降序显示它们的值
count = 0
for i in (-1 * similarity).argsort():
if id_to_word[i] == query:
continue
print(f"{id_to_word[i]}: {similarity[i]}")
count += 1
if count >= top:
return
"""当某个单词被作为查询词时,将与这个查询词相似的单词按降序显示出来"""
import sys
sys.path.append("..")
from common.util import preprocess, create_co_matrix, most_similarity
text = "You say goodbye and I say hello." # 文本
corpus, word_to_id, id_to_word = preprocess(text) # 文本语料预处理
vocab_size = len(word_to_id) # 词汇大小
matrix = create_co_matrix(corpus, vocab_size) # 生成共现矩阵
# 将与单词"you"相似的单词按降序显示出来
most_similarity("you", word_to_id, id_to_word, matrix, top=5)
[query]you
goodbye: 0.7071067691154799
i: 0.7071067691154799
hello: 0.7071067691154799
say: 0.0
and: 0.04. 基于计数的方法的改进
4.1 点互信息
针对高频词汇(出现次数很多的单词),根据共现矩阵统计两个单词同时出现的次数,可能会存在相关性误差。比如:我们来考虑某个语料库中 the 和 car 共现的情况。
在这种情况下,我们会看到很多 “...the car...” 这样的短语。因此,它们的共现次数将会很大。另外,car 和 drive 也明显有很强的相关性。但是,如果只看单词的出现次数,那么与 drive 相比,the 和 car 的相关性更强。这意味着,仅仅因为 the 是个常用词,它就被认为与 car 有很强的相关性。
点互信息(Pointwise Mutual Information,PMI):对于随机变量 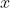 和
和 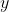 ,它们的 PMI 定义如下:
,它们的 PMI 定义如下:
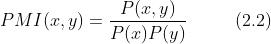
:单词
在语料库中出现的概率。
:单词
在语料库中出现的概率。
:单词
和
同时在语料库中出现的概率。
注:PMI 的值越高,表明相关性越强。
PMI 示例:假设某个语料库中有 10000 个单词,其中单词 the 出现了 100 次,单词 the 和 car 同时出现了 10 次,分别计算 P("the") 和 P("the", "car")。
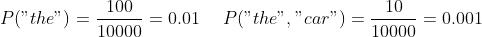
使用共现矩阵(其元素表示单词共现的次数)重写式 (2.2),根据共现矩阵求 PMI:
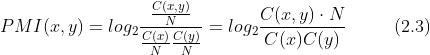
:共现矩阵。
:单词
和
的共现次数。
:单词
的出现次数。
:单词
的出现次数。
根据共现矩阵求 PMI 示例:假设语料库中的单词数量(N)为 10000,the 出现 1000 次,car 出现 20 次,drive 出现 10 次,the 和 car 共现 10 次,car 和 drive 共现 5 次。
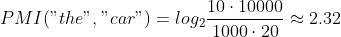
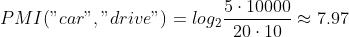
PMI 存在的问题:当两个单词的共现次数为 0 时,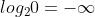 。
。
正的点互信息(Positive PMI,PPMI):
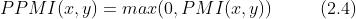
当 PMI 是负数时,将其视为 0,这就可以将单词间的相关性表示为大于 0 的实数。
使用 Python 实现将共现矩阵转化为 PPMI 矩阵:
4.2 降维
以上是关于python深度学习进阶-自然语言处理-自然语言和单词的分布式表示的主要内容,如果未能解决你的问题,请参考以下文章