python自然语言处理入门-词典分词

Posted 2021-05-17 诗雨时

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了python自然语言处理入门-词典分词相关的知识，希望对你有一定的参考价值。

自然语言处理入门-词典分词

摘要

中文分词指的是将一段文本拆分为一系列单词的过程，这些单词顺序拼接后等于原文本。
词典分词是最简单、最常见的分词算法，仅需一部词典和一套查词典的规则即可。
给定一部词典，词典分词就是一个确定的查词与输出的规则系统。

1. 什么是词

1.1 词的定义

语言学定义：具备独立意义的最小单位。

基于词典的中文分词中的定义：词典中的字符串就是词。

1.2 词的性质——齐夫定律

齐夫定律：哈弗大学语言学家乔治 . 金斯利 . 齐夫于 1949 年发表，一个单词的词频与它的词频排名成反比。

实验：基于 MSR 语料库（微软亚洲研究院语料库）上的统计结果验证 “齐夫定律”。

[('，', 173173), ('的', 128146), ('。', 81757), ('、', 40695), ('在', 28445), ('了', 27103), ('和', 24398), ('是', 18068), ('”', 16867), ('“', 16686), ('一', 11503), ('有', 9905), ('对', 9654), ('为', 9516), ('中', 9444), ('上', 8408), ('不', 7222), ('这', 7198), ('与', 7197), ('他', 7062), ('就', 6485), ('人', 6338), ('到', 6316), ('等', 6008), ('：', 5988), ('发展', 5976), ('说', 5973), ('也', 5801), ('要', 5660), ('将', 5651)]

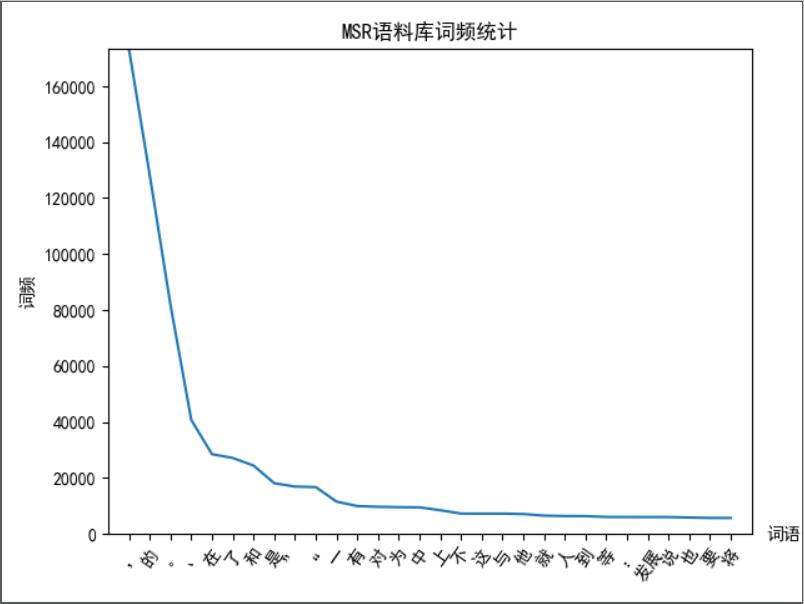
横坐标：按词频降序排列的前 30 个常用词；纵坐标：相应的词频。

这条曲线大致符合 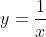$y=\\frac{1}{x}$ ，即满足幂律分布（power law distribution），也称长尾效应、二八原则、马太效应等。也就是说，虽然存在很多生词，但越靠后词频越小，趋近于 0。

2. 词典

互联网上公开的中文词典：搜狗实验室发布的互联网词库（SogouW，其中有 15 万个词条）、清华大学开放中文词库（THUOCL）、HanLP 词典。

2.1 HanLP 词典

以HanLP 附带的迷你核心词典为例，其路径为 "site-packages/pyhanlp/static/data/dictionary/CoreNatureDictionary.txt"。这是一个纯文本文件，用记事本打开后，可以观察到如下格式：

希望  v  7685   vn 616
希望村    ns 2
希杰 nrf    2
希泊妮    nz 2
希波克拉底  nrf    1

HanLP 中的词典格式：一种以空格分隔的表格形式，第一列是单词本身，之后每两列分别表示词性与相应的词频。比如第 1 行 “希望 v 7685 vn 616” 表示 “希望” 这个词以动词的身份出现了 7685 次，以动名词的身份出现了 616 次。

如果单词本身有空格，那该怎么办呢？比如 iPhone X、Macbook Pro，此时可以使用英文逗号分隔的 .csv 文件。

iPhone X, n, n

Macbook Pro, n , 1

注：如果用户的词语都是名词，或者不关心词性的话，可以省略词性部分。

2.2 词典的加载

"""
加载HanLP中的mini词库
"""

from pyhanlp import JClass, HanLP


def load_dictionary():
    """
    加载HanLP中的mini词库
    :return: 一个set形式的词库
    """
    # 根据 Java 路径名获取 HanLp 中的 IOUtil 工具类
    IOUtil = JClass("com.hankcs.hanlp.corpus.io.IOUtil")
    # 获取 HanLP 的配置项 Config 中的词典路径
    path = HanLP.Config.CoreDictionaryPath.replace(".text", ".mini.text")
    # 加载词典数据，参数可以传一个路径字符串，也可以传一个路径字符串列表，返回一个 Java Map 对象
    # dic = IOUtil.loadDictionary(path)
    dic = IOUtil.loadDictionary([path])
    # 将 Java Map 对象转换为 Python 原生的 Set 对象，并返回
    return set(dic.keySet())


if __name__ == "__main__":
    dic = load_dictionary()
    print(len(dic))
    print(list(dic)[0])

153091
沙特阿尔阿赫利

3. 切分算法

词典查找的规则：完全切分、正向最长匹配、逆向最长匹配、双向最长匹配。

3.1 完全切分

完全切分：找出一段文本中的所有单词。

"""完全切分的中文分词算法"""

import os
import sys
sys.path.append(os.pardir)  # 为了导入父目录的文件而进行的设定

from ch02.utifily import load_dictionary


def completely_segment(text, dic):
    """
    完全切分的中文分词算法
    :param text: 待切分的文本
    :param dic: 词典
    :return: 单词列表
    """
    word_list = []
    for i in range(len(text)):                   # i从0遍历到text的最后一个字符的下标
        for j in range(i + 1, len(text) + 1):    # j遍历[i+1, len(text)+1] 区间
            word = text[i: j]                    # 去除连续区间[i, j]对应的字符串
            if word in dic:                      # 如果在词典中，则认为是一个词
                word_list.append(word)
    return word_list


if __name__ == "__main__":
    dic = load_dictionary()
    print(completely_segment("商品和服务", dic))
    print(completely_segment("就读北京大学", dic))

['商', '商品', '品', '和', '和服', '服', '服务', '务']
['就', '就读', '读', '北', '北京', '北京大学', '京', '大', '大学', '学']

3.2 正向最长匹配

最长匹配算法：在以某个下标为起点递增查词的过程中，优先输出更长的词，这种规则被称为最长匹配算法。

正向最长匹配：在以某个下标为起点从前往后递增查词的过程中，优先输出更长的词，这种规则被称为正向最长匹配。

"""正向最大匹配的中文分词算法"""

import os
import sys
sys.path.append(os.pardir)  # 为了导入父目录的文件而进行的设定

from ch02.utifily import load_dictionary


def forward_segment(text, dictionary):
   """
    正向最大匹配的中文分词算法
    :param text: 待切分的文本
    :param dictionary: 词典
    :return: 单词列表
    """
    word_list = []
    i = 0
    while i < len(text):
        longest_word = text[i]                       # 当前扫描位置的单词
        for j in range(i + 1, len(text) + 1):        # 所有可能的结尾
            word = text[i: j]                        # 从当前位置到结尾的连续字符串
            if word in dictionary:                   # 在词典中
                if len(word) > len(longest_word):    # 并且更长
                    longest_word = word              # 则更优先输出
        word_list.append(longest_word)               # 输出最长词
        i += len(longest_word)                       # 正向扫描
    return word_list


if __name__ == "__main__":
    dictionary = load_dictionary()
    print(forward_segment("就读于北京大学", dictionary))
    print(forward_segment("研究生命的起源", dictionary))

['项目', '的', '研究']
['商品', '和服', '务']
['研究生', '命', '起源']
['当下', '雨天', '地面', '积水']
['结婚', '的', '和尚', '未', '结婚', '的']
['欢迎', '新', '老师', '生前', '来', '就餐']

3.3 逆向最长匹配

逆向最长匹配：在以某个下标为起点从后往前递增查词的过程中，优先输出更长的词，这种规则被称为逆向最长匹配。

"""逆向最大匹配的中文分词算法"""

import os
import sys
sys.path.append(os.pardir)  # 为了导入父目录的文件而进行的设定

from ch02.utifily import load_dictionary


def backward_segment(text, dictionary):
    """"
    逆向最大匹配的中文分词算法
    :param text: 待切分的文本
    :param dictionary: 词典
    :return: 单词列表
    """
    word_list = []
    i = len(text) - 1
    while i >= 0:                                     # 扫描位置作为终点
        longest_word = text[i]                       # 扫描位置的单词
        for j in range(0, i):                        # 遍历[0, i]区间作为待查询词语的起点
            word = text[j: i+1]                      # 取[j, i+1]区间作为待查询单词
            if word in dictionary:                   # 在词典中
                if len(word) > len(longest_word):    # 越长优先级越高
                    longest_word = word
                    break
        word_list.insert(0, longest_word)            # 逆向扫描，因此越先查出的单词在位置上越靠后
        i -= len(longest_word)                       # 正向扫描
    return word_list


if __name__ == "__main__":
    dictionary = load_dictionary()
    print(backward_segment("项目的研究", dictionary))
    print(backward_segment("商品和服务", dictionary))
    print(backward_segment("研究生命起源", dictionary))
    print(backward_segment("当下雨天地面积水", dictionary))
    print(backward_segment("结婚的和尚未结婚的", dictionary))
    print(backward_segment("欢迎新老师生前来就餐", dictionary))

['项', '目的', '研究']
['商品', '和', '服务']
['研究', '生命', '起源']
['当', '下雨天', '地面', '积水']
['结婚', '的', '和', '尚未', '结婚', '的']
['欢', '迎新', '老', '师生', '前来', '就餐']

3.4 双向最长匹配

双向最长匹配：融合了正向最长匹配和逆向最长匹配的复杂规则集，流程如下。

（1）同时执行正向和逆向最长匹配，若两者的词数不同，则返回词数更少的那一个。

（2）否则，返回两者中单字更少的那一个。当单字数也相同时，优先返回逆向最长匹配的结果。3.5 速度测评

这种规则的出发点来自语言学上的启发——汉语中单字词的数量要远远小于非单字词。因此，算法应当尽量减少结果中的单字，保留更多的完整词语，这样的算法也称为启发式算法。

"""双向最长匹配"""

import os
import sys
sys.path.append(os.pardir)  # 为了导入父目录的文件而进行的设定

from ch02.utifily import load_dictionary
from ch02.forward_segment import forward_segment
from ch02.backward_segment import backward_segment


def count_single_char(word_list):
    """
    统计单字成词的个数
    :param word_list: 单词列表
    :return: 单字个数
    """
    count = 0
    for word in word_list:
        if len(word) == 1:
            count += 1
    # return sum(1 for word in word_list if len(word) == 1)
    return count


def bidirectional_segment(text, dictionary):
    """"
    双向最大匹配的中文分词算法
    :param text: 待切分的文本
    :param dictionary: 词典
    :return: 单词列表
    """

    forward_list = forward_segment(text, dictionary)
    backward_list = backward_segment(text, dictionary)

    if len(forward_list) < len(backward_list):    # 词数更少优先级更高
        return forward_segment
    elif len(forward_list) > len(backward_list):
        return backward_list
    elif len(forward_list) == len(backward_list):
        if count_single_char(forward_list) < count_single_char(backward_list):    # 单字数更少优先级更高
            return forward_list
        else:    # 词数相等、单字数相等，逆向匹配优先级更高
            return backward_list


if __name__ == "__main__":
    dictionary = load_dictionary()
    print(bidirectional_segment("项目的研究", dictionary))
    print(bidirectional_segment("商品和服务", dictionary))
    print(bidirectional_segment("研究生命起源", dictionary))
    print(bidirectional_segment("当下雨天地面积水", dictionary))
    print(bidirectional_segment("结婚的和尚未结婚的", dictionary))
    print(bidirectional_segment("欢迎新老师生前来就餐", dictionary))

3.5 效果测评

**表 2-1 4种切分规则的效果对比**
序号	原文	完全切分	正向最长匹配	逆向最长匹配	双向最长匹配
1	项目的研究	['项', '项目', '目', '目的', '的', '研', '研究', '究']	['项目', '的', '研究']	['项', '目的', '研究']	['项', '目的', '研究']
2	商品和服务	['商', '商品', '品', '和', '和服', '服', '服务', '务']	['商品', '和服', '务']	['商品', '和', '服务']	['商品', '和', '服务']
3	研究生命起源	['研', '研究', '研究生', '究', '生', '生命', '命', '起', '起源', '源']	['研究生', '命', '起源']	['研究', '生命', '起源']	['研究', '生命', '起源']
4	当下雨天地面积水	['当', '当下', '下', '下雨', '下雨天', '雨', '雨天', '天', '天地', '地', '地面', '面', '面积', '积', '积水', '水']	['当下', '雨天', '地面', '积水']	['当', '下雨天', '地面', '积水']	['当下', '雨天', '地面', '积水']
5	结婚的和尚未结婚的	['结', '结婚', '婚', '的', '和', '和尚', '尚', '尚未', '未', '结', '结婚', '婚', '的']	['结婚', '的', '和尚', '未', '结婚', '的']	['结婚', '的', '和', '尚未', '结婚', '的']	['结婚', '的', '和', '尚未', '结婚', '的']
6	欢迎新老师生前来就餐	['欢', '欢迎', '迎', '迎新', '新', '老', '老师', '师', '师生', '生', '生前', '前', '前来', '来', '就', '就餐', '餐']	['欢迎', '新', '老师', '生前', '来', '就餐']	['欢', '迎新', '老', '师生', '前来', '就餐']	['欢', '迎新', '老', '师生', '前来', '就餐']

实验通过对 6 个中文句子进行切分，正向最长匹配的正确率为 1/6，逆向最长匹配的正确率为 4/6，双向最长匹配的正确率为 3/6。由此规则系统的脆弱可见一斑。规则集的维护有时是拆东墙补西墙，有时是帮倒忙。

3.5 速度测评

实验：基于词典分词中文分词的 4 中规则，分别对文本 “江西鄱阳湖干枯，中国最大淡水湖变成大草原。” 进行 10000 次的分词操作，对分词速度进行对比。

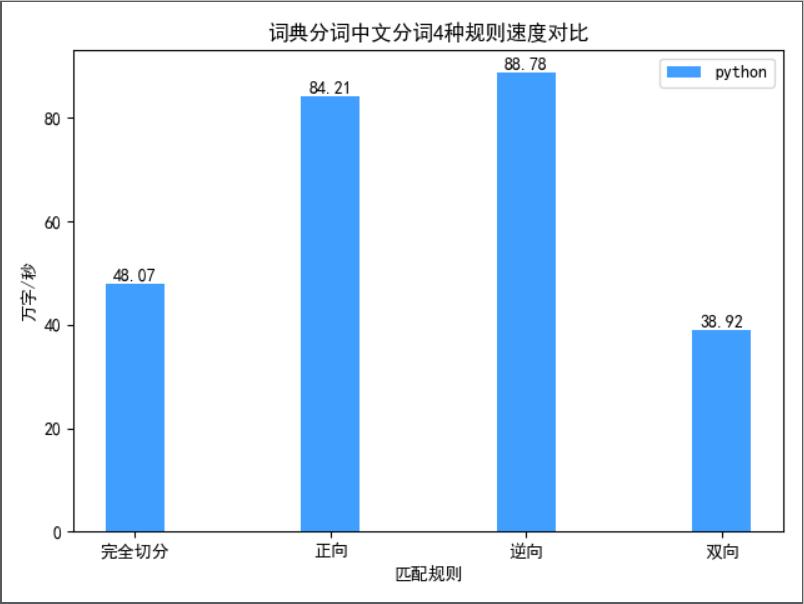
正向匹配和逆向匹配的速度差不多，是双向的两倍。这在意料之中，因为双向匹配做了两倍的工作。

Python 代码：


"""速度测评"""

import os
import sys
import time
from matplotlib import pyplot as plt
sys.path.append(os.pardir)  # 为了导入父目录的文件而进行的设定

from ch02.utifily import load_dictionary
from ch02.completely_segment import completely_segment
from ch02.forward_segment import forward_segment
from ch02.backward_segment import backward_segment
from ch02.bidirectional_segment import bidirectional_segment


def evaluate_speed(segment, text, dictionary):
    """
    评测速度
    :param segment: 匹配规则
    :param text: 待切分的文本
    :param dictionary: 词典
    :return: 运行速度
    """
    start_time = time.time()
    for i in range(pressure):
        segment(text, dictionary)
    elapsed_time = time.time() - start_time
    return len(text) * pressure / 10000 / elapsed_time


if __name__ == "__main__":
    text = "江西鄱阳湖干枯，中国最大淡水湖变成大草原。"
    pressure = 10000
    segment_list = [{
        "name": "完全切分",
        "segment": completely_segment
    }, {
        "name": "正向",
        "segment": forward_segment
    }, {
        "name": "逆向",
        "segment": backward_segment
    }, {
        "name": "双向",
        "segment": bidirectional_segment
    }]
    dic = load_dictionary()
    count_list = []
    x_list = []
    for segment in segment_list:
        speed = evaluate_speed(segment.get("segment"), text, dic)
        count_list.append(speed)
        x_list.append(segment.get("name"))
    plt.rcParams["font.sans-serif"] = ['SimHei']  # 正常显示中文
    plt.rcParams["axes.unicode_minus"] = False  # 正常显示负号
    plt.bar(x_list, count_list, width=0.3, color="#409eff", label="python")
    plt.legend()
    plt.xlabel("匹配规则")
    plt.ylabel("万字/秒")
    plt.title("词典分词中文4种规则速度对比")
    for a, b in zip(x_list, count_list):  # 柱子上的数字显示
        plt.text(a, b, "%.2f" % b, ha="center", va="bottom", fontsize=10)
    plt.show()

4. 字典树

4.1 什么是字典树

字典树（trie树、前缀树）：一种字符串上的树形数据结构。一个典型的字典树如图 2-3 所示。

字典树中每条边都对应一个字，从根节点往下的路径构成一个个字符串。

字典树并不直接在节点上存储字符串，而是将词语视作根节点到某节点之间的一条路径，并在终点节点（蓝色）上做个标记 “该节点对应词语的结尾”。

字符串就是一条路径，要查询一个单词，只需顺着这条路径从根节点往下走。如果能走到特殊标记的节点，则说明该字符串在集合中，否则说明不存在。

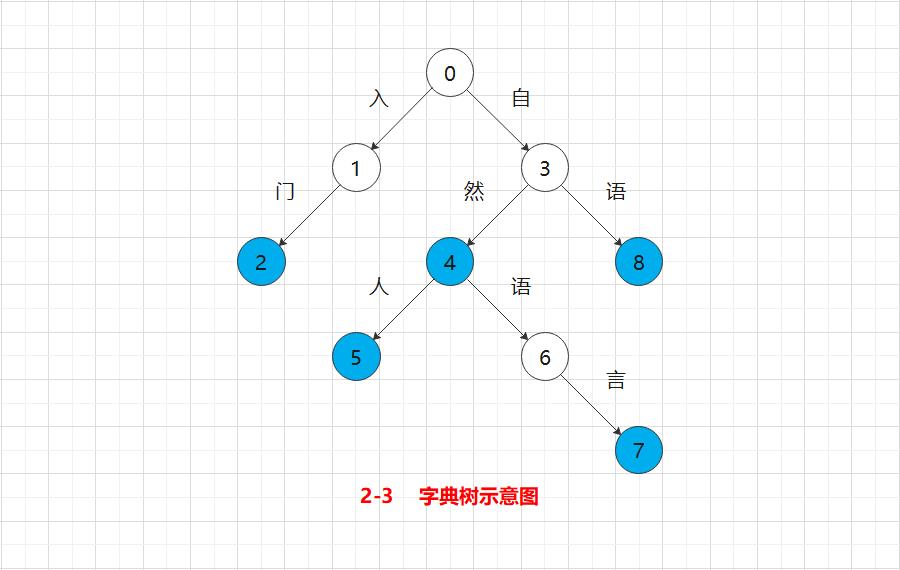
其中，蓝色标记着该节点是一个词的结尾，数字是人为的编号。这棵树中存储的词典如表 2-2 所示，我们可以顺着表 2-2 所示的路径找到对应的单词。

**表 2-2 字典树中的词语与路径**
词语	路径
入门	0-1-2
自然	0-3-4
自然人	0-3-4-5
自然语言	0-3-4-6-7
自语	0-3-8

不光是集合（Set），字典树也可以实现映射（map），只需将相应的值悬挂在键的终点节点上即可（图 2-3 的蓝色节点不一定是叶子结点）。

当词典大小为 n 时，虽然最坏情况下字典树的复杂度依然是（假设子节点用对数复杂度的数据结构存储，所有词语都是单字），但它的实际速度比二分查找快。这是因为随着路径的深入，前缀匹配是递进的过程，算法不必比较字符串的前缀。

4.2 字典树的节点及其增删改查实现

由图 2-3 所知，每个节点都应该至少知道自己的子节点与对应的边，以及自己是否对应一个词。如果要实现映射而不是集合的话，还需要知道自己对应的值。

从确定有限状态自动机（DFA）的角度来讲，每个节点都是一个状态，状态表示当前已查询到的前缀。图 2-3 所示的字典树中每个状态对应的前缀如表 2-3 所示。

**表 2-3 字典树状态与对应前缀**
状态	前缀
0	""（空白）
1	入
2	入门
3	自
4	自然
5	自然人
6	自然语
7	自然语言
8	自语

按照某个字符进行状态转移的过程：从父节点到子节点的过程可以看作一次状态转移。

(1) 向父节点询问该字符与子节点的映射关系（一条边）；

(2) 如果父节点有满足条件的边，则状态转移到子节点；

(3) 如果父节点没有满足条件的边，立即失败，查询不到；

(4) 当成功完成了全部转移时，我们就拿到了最后一个状态，询问该状态是否是终点状态（蓝色）；

(5) 如果是，就查到了该单词，否则该单词不存在于词典中。

"""字典树"""


class Node(object):
    """字典树的节点实现"""
    def __init__(self, value) -> None:
        self.children = {}
        self.value = value

    def add_child(self, char, value, overwrite=False):
        child = self.children.get(char)
        if child is None:
            child = Node(value)
            self.children[char] = child
        elif overwrite:
            child.value = value
        return child


class Trie(Node):
    """字典树的增删改查实现"""
    def __init__(self) -> None:
        super().__init__(None)

    def __contains__(self, item):
        return self[item] is not None

    def __getitem__(self, item):
        state = self
        for char in item:
            state = state.children.get(char)
            if state is None:
                return None
        return state.value

    def __setitem__(self, key, value):
        state = self
        for i, char in enumerate(key):
            if i < len(key) - 1:
                state = state.add_child(char, None, False)
            else:
                state = state.add_child(char, value, True)


if __name__ == "__main__":
    trie = Trie()
    # 增
    trie["自然"] = "nature"
    trie["自然人"] = "human"
    trie["自然语言"] = "language"
    trie["自语"] = "talk to oneself"
    trie["入门"] = "introduction"
    assert "自然" in trie
    # 删
    trie["自然"] = None
    assert "自然" not in trie
    # 改
    trie["自然语言"] = "human language"
    assert trie["自然语言"] == "human language"
    # 查
    assert trie["入门"] == "introduction"