RSA加密算法原理
Posted better_hui
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了RSA加密算法原理相关的知识,希望对你有一定的参考价值。
根目录:https://blog.csdn.net/u012391423/article/details/116136906
目录
注意: 下文中 形如 a^b 意思是 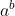
一、可公度线段
1、度量
几何学之父欧几里得在《几何原本》里,这样描述:线段a的长度用线段b来表示,a = b * n , 如果n 是整数,我们称之为b可以度量a。
2、公度
假定线段a 、b , 可以找到线段c ,满足以下条件:
1、m > 0 , n > 0 , 且为整数
2、a = m * c ; b = n * c
我们称之为 a,b是可公度的。c是a、b的一个公度单位,在代数学里我们称之为公约数。
3、最大公度单位
假定线段 a = 12 , b = 16 , 则满足以上条件的 线段c = 1 | 2 | 4 ,这三个取值的c都是线段 a、b的公度单位,其中 c =4 ,是最大的公度单位 , 在代数学里我们称之为最大公约数。
4、求最大公度单位 - 辗转相除法
已知线段a、b , 假定 a>=b 且 a,b可公度, 我们如何求解最大公度单位呢?在几何原本里给出了方法:
c = a / b ,如果c 是整数 ,则c是a,b的最大公度单位,否则 d = b / c , 如果d是整数 , 则d是a,b的最大公度,否则继续循环 ,如此循环直至可以整除为止,最后的除数即是a,b的最大公度单位。
我们成以上循环相处求最大公度单位的方法为辗转相除法

5、不可公度
是否存在线段a,b不可公度呢?答案是肯定的。
例1:
假定线段a,b满足以下条件,是不可公度的 。 a/b = b/(a-b) = 1:0.618 ,黄金比例的两条线段是不可公度的。
例2:
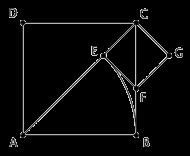
正方形的边长和对角线是不可公度的。让我们画个图来说明这一点。如图,我们试着用辗转相除求出边长 AB 和对角线 AC 的最大公度单位。按照规则,第一步我们应该用 AB 去度量 AC ,假设所得的零头是 EC 。下一步,我们应该用 EC 去度量 AB ,或者说用 EC 去度量 BC (反正正方形各边都相等)。让我们以 EC 为边作一个小正方形 CEFG ,容易看出 F 点将正好落在 BC 上,同时三角形 AEF 和三角形 ABF 将会由于 HL 全等。因此, EC = EF = BF 。注意到 BC 上已经有一段 BF 和 EC 是相等的了,因而我们用 EC 去度量 BC 所剩的零头,也就相当于用 EC 去度量 FC 所剩的零头。结果又回到了最初的局面——寻找正方形的边长和对角线的公度单位。因而,辗转相除永远不会结束。线段 AB 的长度和线段 AC 的长度不能公度,它们处于两个不同的世界中。
二、中国剩余定理
1、互质
如果两个正整数的最大公约数为1,我们说这两个数互质。如果a 与 b 互质:
这就意味着: a/b 已经不能再约分了;
也意味着: a × b 的棋盘对角线不会经过中间的任何交叉点;
意味着: 循环长度分为a 和 b的周期事件,最短周期是a*b

对于任意两个数 , 他们的乘积一定是他们的公倍数,而互质的两个数是其中的特例,互质的两数乘积是他们的最小公倍数。
我们还可以引申为更深的结论:a 和 b的最大公约数 和 最小公倍数的乘积, 一定等于 a 和 b的乘积。
举例:
a= 4 , b = 6 , 最大公约数 = 2 , 最小公倍数 = 12 , 乘积 2 * 12 = a * b = 4 * 6
2、中国剩余定理
很多复杂的数学现象都与互质有关,《孙子算经》有问曰:“今有物,不知其数。三三数之剩二,五五数之剩三,七七数之剩二。问物几何?答曰:二十三。” 当然这个问题有很多答案:23,128,233,338。。。观其规律,符合工时23 + 105 * n 的数都满足。事实上不管物体总数模3,模5,模7的结果分别是多少,在0-104当中总能找到唯一的解;我们在这个解的基础上加上105的整数倍,可以得到其他所有的整数解,我们将其表述为“中国剩余定理”:
给出m个两两互质的整数,他们的乘积为P ; 假定有一个未知数M ,我们已知M 分别 除以这m个数的余数 , 那么在0 到 P-1的范围内,我们可以唯一的确定这个数M。
3、循环周期
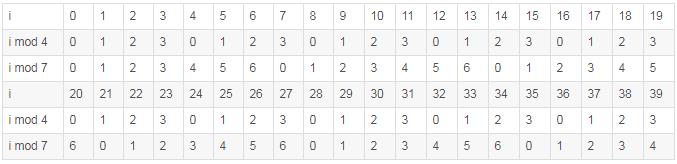
我们以两个除数的情况为例,梳理下剩余定理的其他规律。假定这两个数分别是4、7。下标枚举了各自然数mod 4 和 mod 7的结果。
i mod 4 的余数以4为周期循环
i mod 7 的余数以7位周末循环。
因为4 与 7 互质 , 他们的最小公倍数是28 , 因而 (i mod 4 , i mod 7 ) 的循环周期是28,不会更短。因此,当i 从0递增至27时 , (i mod 4 , i mod 7)的值始终没有出现重复,也就是只有28种组合。每个特定的余数组合都在前28先出现且仅出现一次。在此之后,每一组特定组合,都以28位周期重复出现,这也是中国剩余定理的内容。
4、门限方案
中国剩余定理有许多应用。我们假定这样一个场景:总部打算把一份秘密文件发送给 5 名特工,但直接把文件原封不动地发给每个人,很难保障安全性。万一有特工背叛或者被捕,把秘密泄露给了敌人怎么办?于是就有了电影和小说中经常出现的情 节:把绝密文件拆成 5 份, 5 名特工各自只持有文件的 1/5 。不过,原来的问题并没有彻底解决,我们只能祈祷坏人窃取到的并不是最关键的文件片段。因此,更好的做法是对原文件进行加密,每名特工只持有密码的 1/5 ,这 5 名特工需要同时在场才能获取文件全文。但这也有一个隐患:如果真的有特工被抓了,当坏人们发现只拿到其中一份密码没有任何用处的同时,特工们也会因为少一 份密码无法解开全文而烦恼。此时,你或许会想,是否有什么办法能够让特工们仍然可以恢复原文,即使一部分特工被抓住了?换句话说,有没有什么密文发布方 式,使得只要 5 个人中半数以上的人在场就可以解开绝密文件?这样的话,坏人必须要能操纵半数以上的特工才可能对秘密文件造成实质性的影响。这种秘密共享方式被称为 (3, 5) 门限方案,意即 5 个人中至少 3 人在场才能解开密文。
利用中国剩余定理,我们可以得到一种巧妙的方案。回想中国剩余定理的内容:给定 m 个两两互质的整数,它们的乘积为 P ;假设有一个未知数 M ,如果我们已知 M 分别除以这 m 个数所得的余数,那么在 0 到 P – 1 的范围内,我们可以唯一地确定这个 M 。我们可以想办法构造这样一种情况, n 个数之中任意 m 个的乘积都比 M 大,但是任意 m – 1 个数的乘积就比 M 小。这样,任意 m 个除数就能唯一地确定 M ,但 m – 1 个数就不足以求出 M 来。 Mignotte 门限方案就用到了这样一个思路。我们选取 n 个两两互质的数,使得最小的 m 个数的乘积比最大的 m – 1 个数的乘积还大。例如,在 (3, 5) 门限方案中,我们可以取 53 、 59 、 64 、 67 、 71 这 5 个数,前面 3 个数乘起来得 200128 ,而后面两个数相乘才得 4757 。我们把文件的密码设为一个 4757 和 200128 之间的整数,比如 123456 。分别算出 123456 除以上面那 5 个数的余数,得到 19 、 28 、 0 、 42 、 58 。然后,把 (53, 19) 、 (59, 28) 、 (64, 0) 、 (67, 42) 、 (71, 58) 分别告诉 5 名特工,也就是说特工 1 只知道密码除以 53 余 19 ,特工 2 只知道密码除以 59 余 28 ,等等。这样,根据中国剩余定理,任意 3 名特工碰头后就可以唯一地确定出 123456 ,但根据 2 名特工手中的信息只能得到成百上千个不定解。例如,假设我们知道了 x 除以 59 余 28 ,也知道了 x 除以 67 余 42 ,那么我们只能确定在 0 和 59 × 67 – 1 之间有一个解 913 ,在 913 的基础上加上 59 × 67 的整倍数,可以得到其他满足要求的 x ,而真正的 M 则可以是其中的任意一个数。
不过,为了让 Mignotte 门限方案真正可行,我们还需要一种根据余数信息反推出 M 的方法。换句话说,我们需要有一种通用的方法,能够回答《孙子算经》中提出的那个问题。我们会在下一节中讲到。
三、扩展辗转相除
1、九九乘法表里的规律
中国剩余定理是一个非常基本的定理,很多数学现象都可以通过它来解释。比如,我们在背小九九时,3 * 1 , 3 * 2 , 3 * 3 , .... , 3 * 9 ,他们的个位数正好遍历了1到9 的所有情况。7的倍数 , 9的倍数也是如此 。这三个数有什么特殊的地方吗?3、7、9这三个数 都是和 10 互质的 。 以3为例 , 根据中国剩余定理,在 0 - 29 之间 , 一定存在一个数M , 满足 M mod 3 = 0 , M mod 10 = 1 , 也一定存在一个 N , 满足 N mod 3 = 0 , N mod 10 =2 ;而 3 的整倍数正好有9个 ,所以他们的末位正好无重复且无遗漏的遍历了1-9.
这表明, 如果 a 和 n 互质 , 那么 (a * x ) mod n = 1 、 (a * x ) mod n = 2 、 。。。、 (a * x ) mod n = n -1 ,都是有解的。 我们梳理一个统一的公式 :
a、n 互质 ,0< b < n , 那么 a * x mod n = b , x 一定是有解的
我们用中国剩余定理解释一下这个公式 , 我们需要找到一个数 M ,其满足 M mod a = 0 , M mod a = b ,如果 a 、 n , 那么 这个数M一定是存在的,当我们找到M后 , 就可以找到所有满足该公式的M集合(M ± a * n )。
2、扩展辗转相除
其实 , 我们只需要考虑 a * x mod n = 1的方程即可,因为如果接触了这个方程 , 那么 a * x mod n = 2 或者 3 的方程也就自动解开了。假如 a · x mod n = 1 有一个解 x = 100 ,由于 100 个 a 除以 n 余 1 ,自然 200 个 a 除以 n 就余 2 , 300 个 a 除以 n 就余 3 ,等等,等式右边余数不为 1 的方程也都解开了。
我们尝试求解 115x mod 367 = 1 。注意,由于 115 和 367 是互质的,因此方程确实有解。我们解方程的基本思路是,不断寻找 115 的某个倍数以及 367 的某个倍数,使得它们之间的差越来越小,直到最终变为 1 。由于 367 除以 115 得 3 ,余 22 ,因而 3 个 115 只比 367 少 22 。于是, 15 个 115 就要比 5 个 367 少 110 ,从而 16 个 115 就会比 5 个 367 多 5 。好了,真正巧妙的就在这里了: 16 个 115 比 5 个 367 多 5 ,但 3 个 115 比 1 个 367 少 22 ,两者结合起来,我们便能找到 115 的某个倍数和 367 的某个倍数,它们只相差 2 : 16 个 115 比 5 个 367 多 5 ,说明 64 个 115 比 20 个 367 多 20 ,又考虑到 3 个 115 比 1 个 367 少 22 ,于是 67 个 115 只比 21 个 367 少 2 。现在,结合“少 2 ”和“多 5 ”两个式子,我们就能把差距缩小到 1 了: 67 个 115 比 21 个 367 少 2 ,说明 134 个 115 比 42 个 367 少 4 ,而 16 个 115 比 5 个 367 多 5 ,于是 150 个 115 比 47 个 367 多 1 。这样,我们就解出了一个满足 115x mod 367 = 1 的 x ,即 x = 150 。大家会发现,在求解过程,我们相当于对 115 和 367 做了一遍辗转相除:我们不断给出 115 的某个倍数和 367 的某个倍数,通过辗转对比最近的两个结果,让它们的差距从“少 22 ”缩小到“多 5 ”,再到“少 2 ”、“多 1 ”,其中 22, 5, 2, 1 这几个数正是用辗转相除法求 115 和 367 的最大公约数时将会经历的数。因而,算法的步骤数仍然是对数级别的,即使面对上百位上千位的大数,计算机也毫无压力。这种求解方程 a · x mod n = b 的算法就叫做“扩展的辗转相除法”。
3、应用 - 大小杯取水的问题
扩展的辗转相除法有很多应用,其中一个有趣的应用就是大家小时候肯定见过的“倒水问题”。假如你有一个 3 升的容器和一个 5 升的容器(以及充足的水源),如何精确地取出 4 升的水来?为了叙述简便,我们不妨把 3 升的容器和 5 升的容器分别记作容器 A 和容器 B 。一种解法如下:
-
1. 将 A 装满,此时 A 中的水为 3 升, B 中的水为 0 升;
-
2. 将 A 里的水全部倒入 B ,此时 A 中的水为 0 升, B 中的水为 3 升;
-
3. 将 A 装满,此时 A 中的水为 3 升, B 中的水为 3 升;
-
4. 将 A 里的水倒入 B 直到把 B 装满,此时 A 中的水为 1 升, B 中的水为 5 升;
-
5. 将 B 里的水全部倒掉,此时 A 中的水为 1 升, B 中的水为 0 升;
-
6. 将 A 里剩余的水全部倒入 B ,此时 A 中的水为 0 升, B 中的水为 1 升;
-
7. 将 A 装满,此时 A 中的水为 3 升, B 中的水为 1 升;
-
8. 将 A 里的水全部倒入 B ,此时 A 中的水为 0 升, B 中的水为 4 升;
这样,我们就得到 4 升的水了。显然,这类问题可以编出无穷多个来,比如能否用 7 升的水杯和 13 升的水杯量出 5 升的水,能否又用 9 升的水杯和 15 升的水杯量出 10 升的水,等等。这样的问题有什么万能解法吗?有!注意到,前面用 3 升的水杯和 5 升的水杯量出 4 升的水,看似复杂的步骤可以简单地概括为:不断将整杯整杯的 A 往 B 里倒,期间只要 B 被装满就把 B 倒空。由于 3 × 3 mod 5 = 4 ,因而把 3 杯的 A 全部倒进 B 里,并且每装满一个 B 就把水倒掉, B 里面正好会剩下 4 升的水。类似地,用容积分别为 a 和 b 的水杯量出体积为 c 的水,实际上相当于解方程 a · x mod b = c 。如果 c 是 a 和 b 的最大公约数,或者能被它们的最大公约数整除,用扩展的辗转相除便能求出 x ,得到对应的量水方案。特别地,如果两个水杯的容积互质,问题将保证有解。如果 c 不能被 a 和 b 的最大公约数整除,方程就没有解了,怎么办?不用着急,因为很显然,此时问题正好也没有解。比方说 9 和 15 都是 3 的倍数,那我们就把每 3 升的水视作一个单位,于是你会发现,在 9 升和 15 升之间加加减减,倒来倒去,得到的量永远只能在 3 的倍数当中转,绝不可能弄出 10 升的水来。这样一来,我们就给出了问题有解无解的判断方法,以及在有解时生成一种合法解的方法,从而完美地解决了倒水问题。
四、Fermat小定理
1、质数
很多自然数都可以被分解为更小数的乘积,如,12 = 2 * 2 * 3 , 而 2、3都不能再分解了,他们是最基本、纯净的数 , 我们称之为质数或素数。
2、无穷多个质数
关于为什么质数有无穷多个,古希腊的 Euclid 有一个非常漂亮的证明。假设质数只有有限个,其中最大的那个质数为 p 。现在,把所有的质数全部乘起来,再加上 1 ,得到一个新的数 N 。也就是说, N 等于 2 · 3 · 5 · 7 · … · p + 1 。注意到, N 除以每一个质数都会余 1 ,比如 N 除以 2 就会商 3 · 5 · 7 · … · p 余 1 , N 除以 3 就会商 2 · 5 · 7 · … · p 余 1 ,等等。这意味着, N 不能被任何一个质数整除,换句话说 N 是不能被分解的,它本身就是质数。然而这也不对,因为 p 已经是最大的质数了,于是产生了矛盾。这说明,我们刚开始的假设是错的,质数应该有无穷多个。需要额外说明的一点是,这个证明容易让人产生一个误解,即把 头 n 个质数乘起来再加 1 ,总能产生一个新的质数。这是不对的,因为既然我们无法把全部质数都乘起来,那么所得的数就有可能是由那些我们没有乘进去的质数构成的,比如 2 · 3 · 5 · 7 · 11 · 13 + 1 = 30031 ,它可以被分解成 59 × 509
3、最大公约数、最小公倍数
现在假设 a = 36 = 2 * 2 * 3 * 3 , b = 120 = 2 * 2 * 2 * 3 * 5
最大公约数 , 取决于a、b 包含的这种公共质数更少, 比如 2 可以包含 两个 , 3 可以包含一个 , 那么最大公约数 = 2 * 2 * 3 = 12
最小公倍数 , 取决于a、b谁包含的这种质量更多一些。 比如,2、3 、5 都要包含 , 2 最少包含3个 , 3 最少包含2个 , 5 最少包含一个 , 那么最小公倍数 = 2 * 2 * 2 * 3 * 3 * 5 = 360
当最大公约数 与 最小公倍数相乘时 , 相当于把 a 和 b各自包含的质数都乘了一遍, 所以就有这样的推论:如果两数互质, 这两数的乘积就是他们最大公约数与最小公倍数的乘积。
4、费马小定理
假定n是一个质数 , 对于任意数 a , 均满足 (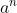 - a ) mod n = 0。例如
- a ) mod n = 0。例如
n = 7 , a = 2 , 那么 (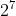 - 2) mod 7 = 0
- 2) mod 7 = 0
Fermat 小定理有一个非常精彩的证明。我们不妨以“ 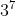 – 3 能被 7 整除”为例进行说明,稍后你会发现,对于其他的情况,道理是一样的。首先,让我来解释一下“循环移位”的意思。想象一个由若干字符所组成的字符串,在一块 大小刚好合适的 LED 屏幕上滚动显示。比方说, HELLOWORLD 就是一个 10 位的字符串,而我们的 LED 屏幕不多不少正好容纳 10 个字符。刚开始,屏幕上显示 HELLOWORLD 。下一刻,屏幕上的字母 H 将会移出屏幕,但又会从屏幕右边移进来,于是屏幕变成了 ELLOWORLDH 。下一刻,屏幕变成了 LLOWORLDHE ,再下一刻又变成了 LOWORLDHEL 。移动到第 10 次,屏幕又会回到 HELLOWORLD 。在此过程中,屏幕上曾经显示过的 ELLOWORLDH, LLOWORLDHE, LOWORLDHEL, … ,都是由初始的字符串 HELLOWORLD 通过“循环移位”得来的。现在,考虑所有仅由 A 、 B 、 C 三个字符组成的长度为 7 的字符串,它们一共有
– 3 能被 7 整除”为例进行说明,稍后你会发现,对于其他的情况,道理是一样的。首先,让我来解释一下“循环移位”的意思。想象一个由若干字符所组成的字符串,在一块 大小刚好合适的 LED 屏幕上滚动显示。比方说, HELLOWORLD 就是一个 10 位的字符串,而我们的 LED 屏幕不多不少正好容纳 10 个字符。刚开始,屏幕上显示 HELLOWORLD 。下一刻,屏幕上的字母 H 将会移出屏幕,但又会从屏幕右边移进来,于是屏幕变成了 ELLOWORLDH 。下一刻,屏幕变成了 LLOWORLDHE ,再下一刻又变成了 LOWORLDHEL 。移动到第 10 次,屏幕又会回到 HELLOWORLD 。在此过程中,屏幕上曾经显示过的 ELLOWORLDH, LLOWORLDHE, LOWORLDHEL, … ,都是由初始的字符串 HELLOWORLD 通过“循环移位”得来的。现在,考虑所有仅由 A 、 B 、 C 三个字符组成的长度为 7 的字符串,它们一共有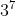 个。如果某个字符串循环移位后可以得到另一个字符串,我们就认为这两个字符串属于同一组字符串。比如说, ABBCCCC 和 CCCABBC 就属于同一组字符串,并且该组内还有其他 5 个字符串。于是,在所有
个。如果某个字符串循环移位后可以得到另一个字符串,我们就认为这两个字符串属于同一组字符串。比如说, ABBCCCC 和 CCCABBC 就属于同一组字符串,并且该组内还有其他 5 个字符串。于是,在所有 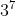 个字符串当中,除了 AAAAAAA 、 BBBBBBB 、 CCCCCCC 这三个特殊的字符串以外,其他所有的字符串正好都是每 7 个一组。这说明,
个字符串当中,除了 AAAAAAA 、 BBBBBBB 、 CCCCCCC 这三个特殊的字符串以外,其他所有的字符串正好都是每 7 个一组。这说明,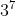 – 3 能被 7 整除。
– 3 能被 7 整除。
排列组合的角度证明
一共7个位置 , 3个字母(A、B、C), 每个位置都有3种放置方法 , 所有的排列情况是, 3 * 3 * 3 * 3 * 3 * 3 * 3 = 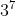 。我们除去其中的特殊情况 :AAAAAAA 、 BBBBBBB 、 CCCCCCC 。
。我们除去其中的特殊情况 :AAAAAAA 、 BBBBBBB 、 CCCCCCC 。
剩下的排列数是 : 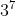 -3 ,
-3 ,
那组合的数量是多少呢 ? 我们认为形如ABCABCA/AABCABC、CAABCAB、BCAABCA、ABCAABC、CABCAAB、BCABCAA、ABCABCA,这7种排列是同一种组合,因为他们都包含 3个A,2个B,2个C 。所以最终的组合数量是:(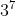 -3 )/ 7 ,且结果肯定是整数
-3 )/ 7 ,且结果肯定是整数
费马小定理的公式
( 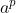 -a ) mod p = 0
-a ) mod p = 0
( 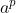 mod p - a mod p) mod p = 0
mod p - a mod p) mod p = 0
我们取个特殊值
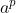 mod p = a mod p
mod p = a mod p
如果n是一个质数,那么对于任意数 a , 随着 i的增加 , a的i次方 除以n的余数将会呈现出长度 n -1 的周期性。这是因为根据前面的结论 : 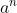 与 a 的差能够被 n 整除,这说明
与 a 的差能够被 n 整除,这说明 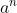 和 a 分别都除以 n 之后将会拥有相同的余数。这表明,依次计算 a 的 1 次方、 2 次方、 3 次方除以 n 的余数,算到 a 的 n 次方时,余数将会变得和最开始相同。另一方面,
和 a 分别都除以 n 之后将会拥有相同的余数。这表明,依次计算 a 的 1 次方、 2 次方、 3 次方除以 n 的余数,算到 a 的 n 次方时,余数将会变得和最开始相同。另一方面, 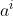 除以 n 的余数,完全由
除以 n 的余数,完全由 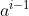 除以 n 的余数决定。比方说,假如我们已经知道
除以 n 的余数决定。比方说,假如我们已经知道 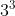 除以 7 等于 3 余 6 ,这表明
除以 7 等于 3 余 6 ,这表明 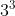 里包含 3 个 7 以及 1 个 6 ;因此,
里包含 3 个 7 以及 1 个 6 ;因此, 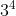 = (
= (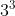 ) * 3 里就包含 9 个 7 以及 3 个 6 ,或者说 9 个 7 以及 1 个 18 。为了得到
) * 3 里就包含 9 个 7 以及 3 个 6 ,或者说 9 个 7 以及 1 个 18 。为了得到 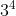 除以 7 的余数,只需要看看 18 除以 7 余多少就行了。可见,要想算出
除以 7 的余数,只需要看看 18 除以 7 余多少就行了。可见,要想算出 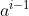 · a 除以 n 的余数,我们不需要完整地知道
· a 除以 n 的余数,我们不需要完整地知道 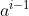 的值,只需要知道
的值,只需要知道 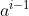 除以 n 的余数就可以了。反正最后都要对乘积取余,相乘之前事先对乘数取余不会对结果造成影响(记住这一点,后面我们还会多次用到)。既然第 n 个余数和第 1 个余数相同,而余数序列的每一项都由上一项决定,那么第 n + 1 个、第 n + 2 个余数也都会跟着和第 2 个、第 3 个余数相同,余数序列从此处开始重复,形成长为 n – 1 的周期。
除以 n 的余数就可以了。反正最后都要对乘积取余,相乘之前事先对乘数取余不会对结果造成影响(记住这一点,后面我们还会多次用到)。既然第 n 个余数和第 1 个余数相同,而余数序列的每一项都由上一项决定,那么第 n + 1 个、第 n + 2 个余数也都会跟着和第 2 个、第 3 个余数相同,余数序列从此处开始重复,形成长为 n – 1 的周期。

注意的是, n – 1 并不见得是最小的周期。下表所示的是 2i 除以 7 的余数情况,余数序列确实存在长度为 6 的周期现象,但实际上它有一个更小的周期, 3 。

那么,如果除数 n 不是质数,而是两个质数的乘积(比如 35 ),周期的长度又会怎样呢?让我们试着看看, 3i 除以 35 的余数有什么规律吧。注意到 5 和 7 是两个不同的质数,因而它们是互质的。根据中国剩余定理,一个数除以 35 的余数就可以唯一地由它除以 5 的余数和除以 7 的余数确定出来。因而,为了研究 3i 除以 35 的余数,我们只需要观察 (3i mod 5, 3i mod 7) 即可
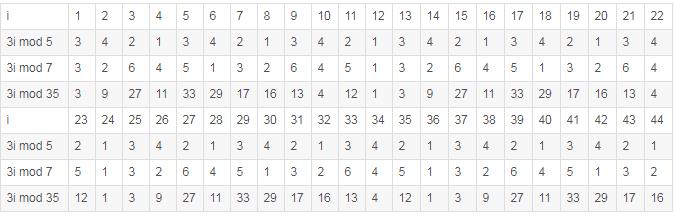
由此 ,我们可以抽象一个规律,假定某个整数 n = p * q , p都是质数,那么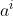 mod n 的余数序列,将以 (p-1)*(q-1)的周期循环往复。
mod n 的余数序列,将以 (p-1)*(q-1)的周期循环往复。
五、公钥加密的可能性
还是讲刚才门限方案的例子,实际上在物理世界是非常容易解决的,总部把绝密文件锁紧一个特殊盒子里,盒子上有三个一模一样的钥匙孔,并配有5把不可能复制的钥匙,然后吧钥匙分发给特工就可以了,只要凑齐3名及以上的特工,同时插入钥匙孔即可打开盒子。但是,这个特殊盒子的方案,在网络世界是不适用的,为了能在网络世界共享秘密,我们需要一种信息层面,只涉及数据交换的方法,Mignotte秘密共享方案应运而生了。
1、一个数学小魔术
小时候我经常在朋友之间表演这么一个数学小魔术:让对方任意想一个三位数,把这个三位数乘以 91 的乘积的末三位告诉我,我便能猜出对方原来想的数是多少。如果对方心里想的数是 123 ,那么对方就计算出 123 × 91 等于 11193 ,并把结果的末三位 193 告诉我。看起来,这么做似乎损失了不少信息,让我没法反推出原来的数。不过,我仍然有办法:只需要把对方告诉我的结果再乘以 11 ,乘积的末三位就是对方刚开始想的数了。你可以验证一下, 193 × 11 = 2123 ,末三位正是对方所想的秘密数字!其实道理很简单, 91 乘以 11 等于 1001 ,而任何一个三位数乘以 1001 后,末三位显然都不变(例如 123 乘以 1001 就等于 123123 )。先让对方在他所想的数上乘以 91 ,假设乘积为 X ;我再在 X 的基础上乘以 11 ,其结果相当于我俩合作把原数乘以了 1001 ,自然末三位又变了回去。然而, X 乘以 11 后的末三位是什么,只与 X 的末三位有关。因此,对方只需要告诉我 X 的末三位就行了,这并不会丢掉信息。站在数论的角度来看,上面这句话有一个更好的解释:反正最后都要取除以 1000 的余数,在中途取一次余数不会有影响(还记得吗,“反正最后都要对乘积取余,相乘之前事先对乘数取余不会对结果造成影响”)。知道原理后,我们可以构造一 个定义域和值域更大的加密解密系统。
虽然这个加密和解密的过程是不对称的,但是并不妨碍我们通过加密的方法,推导出解密的方法来(只是有点小费劲)。以上的例子中,我们知道加密的方法 123 * 91 = 11193 , 截取末三位 193 作为密文,那么猜出对方心里的数相当于求解 形如 91 * x mod 1000 = 193的方程,我们通过辗转相除法,可以很快的求解出来。
2、RSA名字由来
1970年,科学家们开始认真地思考“公钥加密系统”的可能性。 1977 年,来自 MIT 的 Ron Rivest 、 Adi Shamir 和 Leonard Adleman 三个人合写了一篇论文,给出了一种至今仍然安全的公钥加密算法。随后,该算法以三人名字的首字母命名,即 RSA 算法。RSA算法用到了非常犀利的不对称性——大数分解困难。
3、质数判断
判断一个数是不是质数,最笨的方法就是挨个试除,如果一个数p , 不能被比它小的任何数(1除外)整除,那么p就是一个质数,但是这种办法太慢了。费马给了我们一种高效的方法,他基于费马小定理:假定p是一个质数 , 那么对于任意数a , 都满足 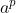 ≡ a (mod p) ,该定理适用于所有的质数 , 但是满足此公式的并不一定都是质数 , 所以我们需要多选几个 数a , 如果都满足此公式,我们就认为p 有很大的几率是质数。
≡ a (mod p) ,该定理适用于所有的质数 , 但是满足此公式的并不一定都是质数 , 所以我们需要多选几个 数a , 如果都满足此公式,我们就认为p 有很大的几率是质数。
4、大数分解困难
我们可以高效的判断一个数是不是质数 , 我们也可以高效的计算两个数的乘积 ,比如两个大的质数19394489 和 27687937 。我们能够很容易计算出 19394489 乘以 27687937 的结果,它等于 536993389579193 ;但是,除了试除法以外,目前还没有什么本质上更有效的方法(也很难找到更有效的方法)能够把 536993389579193 迅速分解成 19394489 乘以 27687937 。这种不对称性很快便成了现代密码学的重要基础。大数分解难题也就成了RSA算法的理论基础。
六、RSA算法
1、构建RSA算法
首先,找到两个质数13、17 ,实际应用时,我们会选两个大的质数。13 * 17 = 221 ,再计算出 (13-1) * (17-1) = 192 , 根据费马小定理,对于任意数a mod 211的余数将以192的周期循环往复,也就是说: a、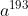 、
、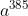 、
、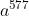 、...... , mod 211 会得到相同的余数。我们选取其中的
、...... , mod 211 会得到相同的余数。我们选取其中的 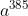 , 385 可以拆分为 11 * 35 ,结合上文的数学小魔术 , 我们要对数 a = 123 (a必须小于211 ),进行加密, 先计算
, 385 可以拆分为 11 * 35 ,结合上文的数学小魔术 , 我们要对数 a = 123 (a必须小于211 ),进行加密, 先计算 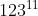 mod 211的余数,得到115 ,看上去,我们根据115 很难还原成 a = 123 ,但是实际上解密的时候 , 我们只需要计算
mod 211的余数,得到115 ,看上去,我们根据115 很难还原成 a = 123 ,但是实际上解密的时候 , 我们只需要计算 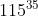 mod 211 余数就会变回123 。 这是因为 加密和解密的过程,相当于共同完成了
mod 211 余数就会变回123 。 这是因为 加密和解密的过程,相当于共同完成了 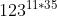 mod 211 的过程 , 而费马小定理:
mod 211 的过程 , 而费马小定理: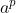 mod p = a mod p 。因此,我们不必知道完成
mod p = a mod p 。因此,我们不必知道完成 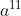 的结果,只需要知道其 mod 211后的余数即可还原数据。
的结果,只需要知道其 mod 211后的余数即可还原数据。
但是这次的情况与上文的小魔术是不通的,知道了加密方法后,构建解密方法是困难的。35之所以能够座位解密的秘钥,是因为加密秘钥11 * 解密秘钥 35 的结果在数列 , 1,193,385,577......中,因此,攻击者可以求解 11 * X mod 192 = 1 ,找到满足要求的秘钥X 。 但是上述方程的关键是192 ,从何而来呢 , 我们需要把211 拆分为13 和 17 的乘积 。 然后计算 192 =(13- 1) * (17 - 1)。根据上文得知 , 大数分解困难,在实际应用时,211替换成一个巨大的数(如,536993389579193 ),拆分是办不到的 , 破解也就无从谈起了
根据以上的原理,我们选择两个充分大的质数 p,q , 并计算出 n = p * q , 再计算出 m = (p-1) * (q-1) ,最后找出 e ,d 使其满足 e * d mod m = 1 。 如何找到 e 和 d 呢?我们随便找一个和m 互质的数, 用作 e , 然后用辗转相除法解得 d , 这样我们就可以加解密了。我们将 e ,n 公之于众,记作公钥 , 用于加密和验证 ;d , n 记作私钥 , 用于解密和签名。
公钥持有者加密的过程 , 密文 = 明文^e mod n
私钥持有者解密的过程 , 明文 = 密文^d mod n
2、效率问题
实际应用时,为了提高安全性,e,d 都是上百位的大数 , 那我们如何计算明文的 e次方 , d次方呢 ?经过了多次计算 , 结果非常大后 , 超过了计算机的内存上限 , 怎么办呢?
第一个问题:我们使用反复相乘的办法 , 比如 a^35= a^34 * a = (a^17)^2 * a = ((a^8)^2 * a )^2 * a = (((a^4)^2)^2 * a )^2 * a = ((((a^2)^2)^2)^2 * a )^2 * a , 7次相乘即可得到结果
第二个问题:我们最终的结果是要做模运算的 , 所以我们可以一边相乘一般做模运算 , 最终的结果, 是不会受到影响的。
3、安全会话的过程
如果 A 、 B 两个人想要建立会话,那么我们可以让 A 先向 B 索要公钥,然后想一个两人今后通话用的密码,用 B 的公钥加密后传给 B ,这将只能由 B 解开。因此,即使窃听者完全掌握了双方约定密码时传递的信息,也无法推出这个密码是多少来。
4、中间人攻击
上述方案让双方在不安全的通信线路上神奇地约定好了密码,一切看上去似乎都很完美了。然而,在这个漂亮的解决方案背后,有一个让人意想不到 的、颇有些喜剧色彩的漏洞——中间人攻击。在 A 、 B 两人建立会话的过程中,攻击者很容易在线路中间操纵信息,让 A 、 B 两人误以为他们是在直接对话。让我们来看看这具体是如何操作的吧。建立会话时, A 首先呼叫 B 并索要 B 的公钥,此时攻击者注意到了这个消息。当 B 将公钥回传给 A 时,攻击者截获 B 的公钥,然后把他自己的公钥传给 A 。接下来, A 随便想一个密码,比如说 314159 ,然后用他所收到的公钥进行加密,并将加密后的结果传给 B 。 A 以为自己加密时用的是 B 的公钥,但他其实用的是攻击者的公钥。攻击者截获 A 传出来的信息,用自己的私钥解出 314159 ,再把 314159 用 B 的公钥加密后传给 B 。 B 收到信息后不会发现什么异样,因为这段信息确实能用 B 的私钥解开,而且确实能解出正确的信息 314159 。今后, A 、 B 将会用 314159 作为密码进行通话,而完全不知道有攻击者已经掌握了密码。
5、CA
怎么封住这个漏洞呢?我们得想办法建立一个获取对方公钥的可信渠道。一个简单而有效的办法就是,建立一个所有人都信任的权威机构,由该权威 机构来储存并分发大家的公钥。这就是我们通常所说的数字证书认证机构,英文是 Certificate Authority ,通常简称 CA 。任何人都可以申请把自己的公钥放到 CA 上去,不过 CA 必须亲自检查申请者是否符合资格。如果 A 想要和 B 建立会话,那么 A 就直接从 CA 处获取 B 的公钥,这样就不用担心得到的是假的公钥了。
新的问题又出来了:那么,怎么防止攻击者冒充 CA 呢? CA 不但需要向 A 保证“这个公钥确实是 B 的”,还要向 A 证明“我确实就是 CA ”。
把加密钥匙和解密钥匙称作“公钥”和“私钥”是有原因的——有时候,私钥也可以用来加密,公钥也可以用来解密。容易看出,既然 a 的 e 次方的 d 次方除以 n 的余数就回到了 a ,那么当然, a 的 d 次方的 e 次方除以 n 的余数也会变回 a 。于是,我们可以让私钥的持有者计算 a 的 d 次方除以 n 的余数,对原文 a 进行加密;然后公钥的持有者取加密结果的 e 次方除以 n 的余数,这也能恢复出原文 a 。但是,用我自己的私钥加密,然后大家都可以解密,这有什么用处呢?不妨来看看这样“加密”后的效果吧:第一,貌似是最荒谬的,大家都可以用我的公钥解出 它所对应的原始文件;第二,很关键的,大家只能查看它背后的原文件,不能越过它去修改它背后的原文件;第三,这样的东西是别人做不出来的,只有我能做出 来。
这些性质正好完美地描述出“数字签名”的实质,刚才的 CA 难题迎刃而解。 CA 首先生成一个自己的公钥私钥对,然后把公钥公之于众。之后, CA 对每条发出去的消息都用自己的私钥加个密作为签名,以证明此消息的来源是真实的。收到 CA 的消息后,用 CA 的公钥进行解密,如果能恢复出 CA 的原文,则说明对方一定是正宗的 CA 。因为,这样的消息只有私钥的持有者才能做出来,它上面的签名是别人无法伪造的。至此为止,建立安全的通信线路终于算是有了一个比较完美的方案。
以上是关于RSA加密算法原理的主要内容,如果未能解决你的问题,请参考以下文章