循环冗余校验(CRC)算法原理分析及实战
Posted “逛丢一只鞋”
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了循环冗余校验(CRC)算法原理分析及实战相关的知识,希望对你有一定的参考价值。
前言
CRC校验(循环冗余校验)是数据通讯中最常采用的校验方式。在嵌入式软件开发中,经常要用到CRC 算法对各种数据进行校验。因此,掌握基本的CRC算法应是嵌入式程序员的基本技能。
从奇偶校验说起
所谓通讯过程的校验是指在通讯数据后加上一些附加信息,通过这些附加信息来判断接收到的数据是否和发送出的数据相同。
比如说RS232串行通讯可以设置奇偶校验位,所谓奇偶校验就是在发送的每一个字节后都加上一位,使得每个字节中1的个数为奇数个或偶数个。
比如我们要发送的字节是0x1a,二进制表示为0001 1010。
采用奇校验,则在数据后补上个0,数据变为0001 1010 0,数据中1的个数为奇数个(3个)
采用偶校验,则在数据后补上个1,数据变为0001 1010 1,数据中1的个数为偶数个(4个)
接收方通过计算数据中1个数是否满足奇偶性来确定数据是否有错。
奇偶校验的缺点也很明显,首先,它对错误的检测概率大约只有50%。也就是只有一半的错误它能够检测出来。另外,每传输一个字节都要附加一位校验位,对传输效率的影响很大。+
因此,在高速数据通讯中很少采用奇偶校验。奇偶校验优点也很明显,它很简单,因此可以用硬件来实现,这样可以减少软件的负担。因此,奇偶校验也被广泛的应用着。
奇偶校验就先介绍到这来,之所以从奇偶校验说起,是因为这种校验方式最简单,而且后面将会知道奇偶校验其实就是CRC 校验的一种(CRC-1)。
累加和校验
另一种常见的校验方式是累加和校验。所谓累加和校验实现方式有很多种,最常用的一种是在一次通讯数据包的最后加入一个字节的校验数据。这个字节内容为前面数据包中全部数据的忽略进位的按字节累加和。比如下面的例子:
我们要传输的信息为: 6、23、4
加上校验和后的数据包:6、23、4、33
这里 33 为前三个字节的校验和。接收方收到全部数据后对前三个数据进行同样的累加计算,如果累加和与最后一个字节相同的话就认为传输的数据没有错误。
累加和校验由于实现起来非常简单,也被广泛的采用。但是这种校验方式的检错能力也比较一般,对于单字节的校验和大概有1/256 的概率将原本是错误的通讯数据误判为正确数据。
之所以这里介绍这种校验,是因为CRC校验在传输数据的形式上与累加和校验是相同的,都可以表示为:通讯数据 校验字节(也可能是多个字节)
初识CRC
循环冗余校验码(cyclic redundancy check)简称CRC(循环码),是一种能力相当强的检错、纠错码,并且实现编码和检码的电路比较简单,常用于串行传送(二进制位串沿一条信号线逐位传送)的辅助存储器与主机的数据通信和计算机网络中。
循环码是指通过某种数学运算实现有效信息与校验位之间的循环校验(而海明码是一种多重校验)。
这种编码基本思想是将要传送的信息M(X)表示为一个多项式L,用L除以一个预先确定的多项式G(X),得到的余式就是所需的循环冗余校验码。
这种校验又称多项式校验。
理论上可以证明循环冗余校验码的检错能力有以下特点:
①可检测出所有奇数位错;
②可检测出所有双比特的错;
③可检测出所有小于、等于校验位长度的突发错。
CRC 算法的基本思想是将传输的数据当做一个位数很长的数。将这个数除以另一个数。得到的余数作为校验数据附加到原数据后面。
模2运算
模2运算是一种二进制算法,CRC校验技术中的核心部分,因此,我们在分析CRC算法之前,必须掌握模2运算的规则。与四则运算相同,模2运算也包括模2加、模2减、模2乘、模2除四种二进制运算。
而且,模2运算也使用与四则运算相同的运算符,即“+”表示模2加,“-”表示模2减,“×”或“·”表示模2乘,“÷”或“/”表示模2除。
与四则运算不同的是模2运算不考虑进位和借位,即模2加法是不带进位的二进制加法运算,模2减法是不带借位的二进制减法运算。
这样,两个二进制位相运算时,这两个位的值就能确定运算结果,不受前一次运算的影响,也不对下一次造成影响。
模2加法
①模2加法运算定义为:
0+0=0 0+1=1 1+0=1 1+1=0
例如:0101+0011=0110
列竖式计算:
0 1 0 1
+0 0 1 1
──────
0 1 1 0
模2减法
②模2减法运算定义为:
0-0=0 0-1=1 1-0=1 1-1=0
例如:0110-0011=0101,列竖式计算:
0 1 1 0
-0 0 1 1
──────
0 1 0 1
模2乘法
③模2乘法运算定义为:
0×0=0 0×1=0 1×0=0 1×1=1
多位二进制模2乘法类似于普通意义上的多位二进制乘法,不同之处在于后者累加中间结果(或称部分积)时采用带进位的加法,而模2乘法对中间结果的处理方式采用的是模2加法。
例如1011×101=100111,列竖式计算:
1 0 1 1
× 1 0 1
──────
1 0 1 1
0 0 0 0
+1 0 1 1
────────
1 0 0 1 1 1
模2除法
④模2除法运算定义为:
0÷1=0 1÷1=1
多位二进制模2除法也类似于普通意义上的多位二进制除法,但是在如何确定商的问题上两者采用不同的规则。后者按带借位的二进制减法,根据余数减除数够减与否确定商1还是商0,若够减则商1,否则商0。多位模2除法采用模2减法,不带借位的二进制减法,因此考虑余数够减除数与否是没有意义 的。
实际上,在CRC运算中,总能保证除数的首位为1,则 模2除法运算的商是由余数首位与除数首位的模2除法运算结果确定。
因为除数首位总是1,按照模2 除法运算法则,那么余数首位是1就商1,是0就商0。
例如1100100÷1011=1110……110,列竖式计算:

校验位的生成
循环冗余校验码由信息码n位和校验码k位构成。k位校验位拼接在n位数据位后面,n+k为循环冗余校验码的字长,又称这个校验码(n+k,n)码。
n位信息位可以表示成为一个报文多项式M(x),最高幂次是xn-1。约定的生成多项式G(x)是一个k+1位的二进制数,最高幂次是xk。将M(x)乘以xk,即左移k位后,除以G(x),得到的k位余数就是校验位。
这里的除法运算是模2除法,即当部分余数首位是1时商取1,反之商取0。然后每一位的减法运算是按位减,不产生借位。
检错计算举例
实际的CRC校验码生成是采用二进制的模2算法(即减法不借位、加法不进位)计算出来的,这是一种异或操作。下面通过一些例子来进一步解释CRC的基本工作原理。假设:
(1)设约定的生成多项式为G(x)=x4+x+1,其二进制表示为10011,共5位,其中k=4。
(2)假设要发送数据序列的二进制为101011(即f(x)),共6位。
(3)在要发送的数据后面加4个0(生成f(x)*xk),也就是数据左移4位,二进制表示为1010110000,共10位。
(4)用生成多项式的二进制表示10011去除乘积1010110000,按模2算法求得余数比特序列为0100(注意余数一定是k位的)。

(5)将余数添加到要发送的数据后面,得到真正要发送的数据的比特流:1010110100(101011 + 0100),其中前6位为原始数据,后4位为CRC校验码。
(6)接收端在接收到带CRC校验码的数据后,如果数据在传输过程中没有出错,将一定能够被相同的生成多项式G(x)除尽,如果数据在传输中出现错误,生成多项式G(x)去除后得到的结果肯定不为0。
生成多项式
从这个例子可以看出,采用了模2的加减法后,不需要考虑借位的问题,所以除法变简单了。最后得到的余数就是CRC 校验字。为了进行CRC运算,也就是这种特殊的除法运算,必须要指定个被除数,在CRC算法中,这个被除数有一个专有名称叫做“生成多项式”。
生成多项式的选取是个很有难度的问题,如果选的不好,那么检出错误的概率就会低很多。好在这个问题已经被专家们研究了很长一段时间了,对于我们这些使用者来说,只要把现成的成果拿来用就行了。
最常用的几种生成多项式如下:
CRC8=X8+X5+X4+X0
CRC-CCITT=X16+X12+X5+X0
CRC16=X16+X15+X2+X0
CRC12=X12+X11+X3+X2+X0
CRC32=X32+X26+X23+X22+X16+X12+X11+X10+X8+X7+X5+X4+X2+X1+X0
有一点要特别注意,文献中提到的生成多项式经常会说到多项式的位宽(Width,简记为W),这个位宽不是多项式对应的二进制数的位数,而是位数减1。
比如CRC8中用到的位宽为8的生成多项式,其实对应得二进制数有九位:100110001。
另外一点,多项式表示和二进制表示都很繁琐,交流起来不方便,因此,文献中多用16进制简写法来表示,因为生成多项式的最高位肯定为1,最高位的位置由位宽可知,故在简记式中,将最高的1统一去掉了,如CRC32的生成多项式简记为04C11DB7实际上表示的是104C11DB7。当然,这样简记除了方便外,在编程计算时也有它的用处。
对于上面的例子,位宽为4(W=4),按照CRC算法的要求,计算前要在原始数据后填上W个0,也就是4个0。
位宽W=1的生成多项式(CRC1)有两种,分别是X1和X1+X0,读者可以自己证明10 对应的就是奇偶校验中的奇校验,而11对应则是偶校验。
因此,写到这里我们知道了奇偶校验其实就是CRC校验的一种特例,这也是我要以奇偶校验作为开篇介绍的原因了。
CRC算法的编程实现
说了这么多总算到了核心部分了。从前面的介绍我们知道CRC校验核心就是实现无借位的除法运算。
下面还是通过一个例子来说明如何实现CRC校验。
假设我们的生成多项式 G(x)为:100110001(一共9bit,k=8,根据前面的简记原则,最高位1忽略,简记为0x31),也就是 CRC-8
则计算步骤如下:
(1) 将CRC寄存器(CRC-8,8-bits,比生成多项式的9bit少1bit,也就是前面的0x31)赋初值0
(2) 在待传输信息流后面加入8个0
(3) While (数据未处理完)
(4) Begin
(5) If (CRC寄存器首位是1)
(6) reg = reg XOR 0x31
(7) CRC寄存器左移一位,读入一个新的数据于CRC寄存器的0 bit的位置。
(8) End
(9) CRC寄存器就是我们所要求的余数。
实际上,真正的CRC 计算通常与上面描述的还有些出入。这是因为这种最基本的CRC除法有个很明显的缺陷,就是数据流的开头添加一些0并不影响最后校验字的结果。这个问题很让人恼火啊,因此真正应用的CRC 算法基本都在原始的CRC算法的基础上做了些小的改动。
所谓的改动,也就是增加了两个概念,第一个是“余数初始值”,第二个是“结果异或值”。
所谓的“余数初始值”就是在计算CRC值的开始,给CRC寄存器一个初始值。
“结果异或值”是在其余计算完成后将CRC寄存器的值在与这个值进行一下异或操作作为最后的校验值。
常见的三种CRC 标准用到个各个参数如下表。
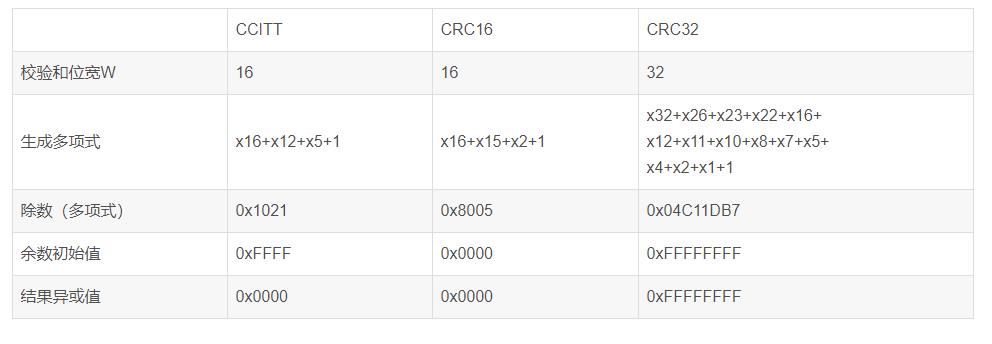
加入这些变形后,常见的算法描述形式就成了这个样子了:
(1) 设置CRC寄存器,并给其赋值为“余数初始值”。
(2) 将数据的第一个8-bit字符与CRC寄存器进行异或,并把结果存入CRC寄存器。
(3) CRC寄存器向右移一位,MSB补零,移出并检查LSB。
(4) 如果LSB为0,重复第三步;若LSB为1,CRC寄存器与0x31相异或。
(5) 重复第3与第4步直到8次移位全部完成。此时一个8-bit数据处理完毕。
(6) 重复第2至第5步直到所有数据全部处理完成。
(7) 最终CRC寄存器的内容与“结果异或值”进行或非操作后即为CRC值。
最高有效位(MSB) 指二进制中最高值的比特。
在16比特的数字音频中,其第1个比特便对16bit的字的数值有最大的影响。
例如,在十进制的15,389这一数字中,相当于万数那1行(1)的数字便对数值的影响最大。
比较与之相反的“最低有效位”(LSB)。
示例性的C代码如下所示,因为效率很低,项目中如对计算时间有要求应该避免采用这样的代码。不过这个代码已经比网上常见的计算代码要好了,因为这个代码有一个crc的参数,可以将上次计算的crc结果传入函数中作为这次计算的初始值,这对大数据块的CRC计算是很有用的,不需要一次将所有数据读入内存,而是读一部分算一次,全读完后就计算完了。这对内存受限系统还是很有用的。
#define POLY 0x1021
/**
* Calculating CRC-16 in 'C'
* @para addr, start of data
* @para num, length of data
* @para crc, incoming CRC
*/
uint16_t crc16(unsigned char *addr, int num, uint16_t crc)
{
int i;
for (; num > 0; num--) /* Step through bytes in memory */
{
crc = crc ^ (*addr++ << 8); /* Fetch byte from memory, XOR into CRC top byte*/
for (i = 0; i < 8; i++) /* Prepare to rotate 8 bits */
{
if (crc & 0x8000) /* b15 is set... */
crc = (crc << 1) ^ POLY; /* rotate and XOR with polynomic */
else /* b15 is clear... */
crc <<= 1; /* just rotate */
} /* Loop for 8 bits */
crc &= 0xFFFF; /* Ensure CRC remains 16-bit value */
} /* Loop until num=0 */
return(crc); /* Return updated CRC */
}
下面对这个函数给出个例子片段代码:
unsigned char data1[] = {'1', '2', '3', '4', '5', '6', '7', '8', '9'};
unsigned char data2[] = {'5', '6', '7', '8', '9'};
unsigned short c1, c2;
c1 = crc16(data1, 9, 0xffff);
c2 = crc16(data1, 4, 0xffff);
c2 = crc16(data2, 5, c2);
printf("%04x\\n", c1);
printf("%04x\\n", c2);
读者可以验算,c1、c2 的结果都为 29b1。上面代码中crc 的初始值之所以为0xffff,是因为CCITT标准要求的除数初始值就是0xffff。
上面的算法对数据流逐位进行计算,效率很低。实际上仔细分析CRC计算的数学性质后我们可以多位计算,最常用的是一种按字节查表的快速算法。
该算法基于这样一个事实:计算本字节后的CRC码,等于上一字节余式CRC码的低8位左移8位,加上上一字节CRC右移 8位和本字节之和后所求得的CRC码。
如果我们把8位二进制序列数的CRC(共256个)全部计算出来,放在一个表里,编码时只要从表中查找对应的值进行处理即可。
按照这个方法,可以有如下的代码
crc.h头文件
/*
crc.h
*/
#ifndef CRC_H_INCLUDED
#define CRC_H_INCLUDED
/*
* The CRC parameters. Currently configured for CCITT.
* Simply modify these to switch to another CRC Standard.
*/
/*
#define POLYNOMIAL 0x8005
#define INITIAL_REMAINDER 0x0000
#define FINAL_XOR_VALUE 0x0000
*/
#define POLYNOMIAL 0x1021
#define INITIAL_REMAINDER 0xFFFF
#define FINAL_XOR_VALUE 0x0000
/*
#define POLYNOMIAL 0x1021
#define POLYNOMIAL 0xA001
#define INITIAL_REMAINDER 0xFFFF
#define FINAL_XOR_VALUE 0x0000
*/
/*
* The width of the CRC calculation and result.
* Modify the typedef for an 8 or 32-bit CRC standard.
*/
typedef unsigned short width_t;
#define WIDTH (8 * sizeof(width_t))
#define TOPBIT (1 << (WIDTH - 1))
/**
* Initialize the CRC lookup table.
* This table is used by crcCompute() to make CRC computation faster.
*/
void crcInit(void);
/**
* Compute the CRC checksum of a binary message block.
* @para message, 用来计算的数据
* @para nBytes, 数据的长度
* @note This function expects that crcInit() has been called
* first to initialize the CRC lookup table.
*/
width_t crcCompute(unsigned char * message, unsigned int nBytes);
#endif // CRC_H_INCLUDED
crc.c服务函数
/*
*crc.c
*/
#include "crc.h"
/*
* An array containing the pre-computed intermediate result for each
* possible byte of input. This is used to speed up the computation.
*/
static width_t crcTable[256];
/**
* Initialize the CRC lookup table.
* This table is used by crcCompute() to make CRC computation faster.
*/
void crcInit(void)
{
width_t remainder;
width_t dividend;
int bit;
/* Perform binary long division, a bit at a time. */
for(dividend = 0; dividend < 256; dividend++)
{
/* Initialize the remainder. */
remainder = dividend << (WIDTH - 8);
/* Shift and XOR with the polynomial. */
for(bit = 0; bit < 8; bit++)
{
/* Try to divide the current data bit. */
if(remainder & TOPBIT)
{
remainder = (remainder << 1) ^ POLYNOMIAL;
}
else
{
remainder = remainder << 1;
}
}
/* Save the result in the table. */
crcTable[dividend] = remainder;
}
} /* crcInit() */
/**
* Compute the CRC checksum of a binary message block.
* @para message, 用来计算的数据
* @para nBytes, 数据的长度
* @note This function expects that crcInit() has been called
* first to initialize the CRC lookup table.
*/
width_t crcCompute(unsigned char * message, unsigned int nBytes)
{
unsigned int offset;
unsigned char byte;
width_t remainder = INITIAL_REMAINDER;
/* Divide the message by the polynomial, a byte at a time. */
for( offset = 0; offset < nBytes; offset++)
{
byte = (remainder >> (WIDTH - 8)) ^ message[offset];
remainder = crcTable[byte] ^ (remainder << 8);
}
/* The final remainder is the CRC result. */
return (remainder ^ FINAL_XOR_VALUE);
} /* crcCompute() */
以上是关于循环冗余校验(CRC)算法原理分析及实战的主要内容,如果未能解决你的问题,请参考以下文章