跳石板---动态规划 / 广度优先遍历

Posted 2021-05-17 满眼*星辰

跳石板

小易来到了一条石板路前，每块石板上从1挨着编号为：1、2、3…
这条石板路要根据特殊的规则才能前进：对于小易当前所在的编号为K的 石板，小易单次只能往前跳K的一个约数(不含1和K)步，即跳到K+X(X为K的一个非1和本身的约数)的位置。 小易当前处在编号为N的石板，他想跳到编号恰好为M的石板去，小易想知道最少需要跳跃几次可以到达。
例如：
N = 4，M = 24：
4->6->8->12->18->24
于是小易最少需要跳跃5次，就可以从4号石板跳到24号石板
输入描述:
输入为一行，有两个整数N，M，以空格隔开。 (4 ≤ N ≤ 100000) (N ≤ M ≤ 100000)
输出描述:
输出小易最少需要跳跃的步数,如果不能到达输出-1
示例1
输入
4 24
输出
5

链接：https://www.nowcoder.com/questionTerminal/4284c8f466814870bae7799a07d49ec8?toCommentId=9196112
来源：牛客网

动态规划

我们先初始化n-m下标石板为最大值，因为我们之后要比较最小步数

我们定义函数，把 i 号石板能跳跃的所有距离，放在顺序表ArrayList当中。

状态定义：
设置动态规划列表arr，arr[i] 表示第 i 号石板所对应的最小步数

转移方程：
如果 arr[i+j] 为默认值，即没有到达过 i 号石板，则arr[i+j] 的值设为arr[i] + 1
不然就对比 arr[i+j] 的步数 和 arr[i] + 1 的步数的最小值，赋予arr[i+j] 号石板的最小步数

初始状态：
arr[n] = 0，最开始的石板步数为0步

返回值：
如果arr[m] 下标为初始状态，即代表没有到达过m号石板，所以输出-1；
否则就输出arr[m] 的值，代表到达m号石板所需要的最小步数。

import java.util.*;

public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        int m = scanner.nextInt();
        int[] arr = new int[m+1];
        //初始化n-m的数据为最大值
        for (int i = n; i < arr.length; i++) {
            arr[i] = Integer.MAX_VALUE;
        }
        arr[n] = 0; //初始状态
        for (int i = n; i < m; i++) {
            //如果没有到达过这个位置，则下一轮循环
            if (arr[i] == Integer.MAX_VALUE) {
                continue;
            }
            //list来记录当前石板能跳的所有距离
            List<Integer> list = piv(i);
            //遍历当前石板所有能跳的距离
            for (int j : list) {
                //大前提，跳到的石板下标不能超过m，否则数组越界
                if(i+j <= m) {
                    //如果跳到的石板之前没有跳到过，则直接+1
                    if(arr[i] == Integer.MAX_VALUE) {
                        arr[i+j] = arr[i] + 1;
                    }else { //否则就取跳到石板步数最小值
                        arr[i+j] = Math.min(arr[i+j],arr[i]+1);
                    }
                }
            }
        }
        //最后判断下标为m的石板的最小步数
        if(arr[m] == Integer.MAX_VALUE) {
            System.out.println(-1);
        }else {
            System.out.println(arr[m]);
        }
    }

    //用来记录石板下标的所有约数
    public static List<Integer> piv(int num) {
        List<Integer> list = new ArrayList<>();
        //这里只需要遍历到i*i <= num即可，因为两数相乘才得到num，小的乘数找到了，对应的大的乘数则为num/i
        for (int i = 2; i*i <= num; i++) {
            if(num % i == 0) {
                list.add(i);
                //这里有可能有i == num/i 的情况，所以只取一次i
                if(i != num/i) {
                    list.add(num/i);
                }
            }
        }
        return list;
    }
}

广度优先遍历

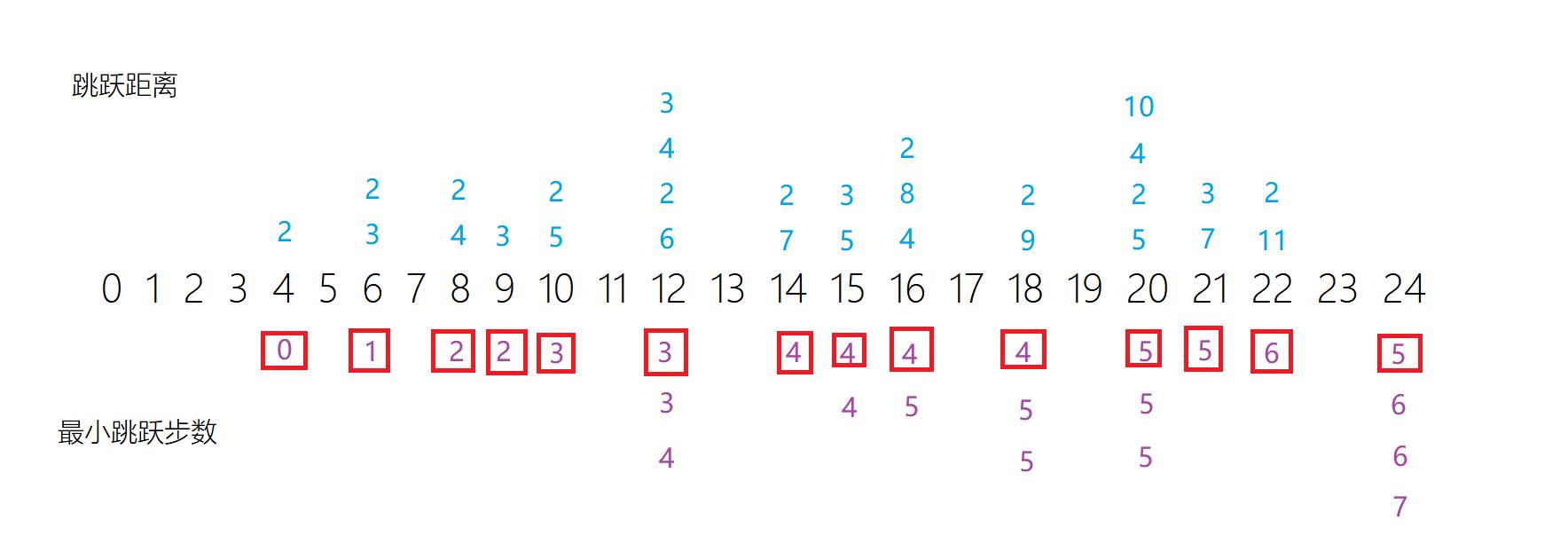
搜过的点不再搜，肯定步数比上一次搜索要大。

我们根据上图也不难看出，最先到达的石板步数是最小的。

import java.util.*;
public class Main {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        int n = in.nextInt();
        int m = in.nextInt();
        Queue<Integer> queue = new LinkedList<>();
        Map<Integer,Integer> map = new HashMap<>();
        map.put(n,0);
        queue.add(n);
        while (!queue.isEmpty()) {
            int head = queue.poll();
            if(head == m) {
                System.out.println(map.get(head));
                return;
            }
            List<Integer> list = yueNum(head);
            for(int i = 0; i < list.size(); i++) {
                int sum = head + list.get(i);
                if(!map.containsKey(sum) && sum <= m) {
                    queue.add(sum);
                    map.put(sum,map.get(head)+1);
                }
            }
        }
        System.out.println(-1);
    }
    public static ArrayList<Integer> yueNum(int n) {
        ArrayList<Integer> list = new ArrayList<>();
        for (int i = 2; i <= Math.sqrt(n); i++) {
            if (n % i == 0) {
                list.add(i);
                if (n / i != i) {
                    list.add(n / i);
                }
            }
        }
        return list;
    }
}