欧拉Euler函数
Posted Chivas_/Regal
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了欧拉Euler函数相关的知识,希望对你有一定的参考价值。
📕概述
🎈概念
欧拉函数是求小于等于某个数num的所有数中,与num互质的个数
🎈思想
其实就是利用了分解质因数
首先我们举个例子
求小于12的数中与12互质的数(也就是12的欧拉值)
首先我们设置12的欧拉值为12本身(1 ~ 12都算进去)
1.12的质因数中有2,所以所有2的倍数都不能与12互质,所以12中要筛去2的倍数也就是12 / 2 = 6个,我们将值缩小为12 * (2 - 1) / 2 = 6
2.12的质因数有3,所以3的倍数都不能与12互质,所以12中要筛去3的倍数也就是12 / 3 = 4个,所以再将值缩小为6 * (3 - 1) / 3 = 4
然后就没有了,所以12的欧拉值为4,有4个12以内的数能跟12互质(也就是1、5、7、11)
🎈朴素定义式
我们设num的欧拉值为phi[num]
在num所有的质因子中,对于每个质因子x,都能使num的欧拉值筛去num / x个,会变成num * (x - 1) / x个
🎈性质
质数num的欧拉值 = num - 1
欧拉函数为积性函数,即当gcd(x, y) == 1时,phi(x * y) = phi(x) * phi(y)
且n为奇质数时,phi(2 * n) = phi(n)
对于x % y == 0,有phi(x * y) = phi(x) * y
📕程序详解
😀朴素暴力
我们可以暴力分解num的质因数,每次对枚举到的质因数x,使phi[num] * (x - 1) / x
inline int PHI(int num){
int res = num;
for(int i = 2; i * i <= n; i ++){
if(num % i == 0){//美剧到了质因子
res = res * (i - 1) / i;
while(num % i == 0) num /= i;//抹掉当前质因子
}
}
if(num > 1) res = res * (num - 1) / num;//抹掉可能出现的剩的一个质因子
return res;
}
此方法在建立1 ~ n的欧拉值时所用时间逼近O(n^2),所以我们需要更快的方法
在学习下面两个之前,如果不懂埃氏筛与欧拉筛的可以点击此处--------传送门
😀埃氏筛欧拉值
利用了埃氏筛的思想
枚举1 ~ n,如果枚举到的是质数(没被筛过)
每个质数的倍数的欧拉值都可以被当前质数作为质因子筛一遍
const int maxn;
int phi[maxn];//欧拉值
inline void GET_PHI(){
for(int i = 0; i <= maxn; i ++) phi[i] = i;//初始化为本身,因为每个质数的第一次筛都可以变成当前数-1
for(int i = 2; i <= maxn; i ++){
if(phi[i] == i){//没有被筛过
for(int j = i; j <= maxn; j += i)
phi[j] = phi[j] * (i - 1) / i;//当前j是以i作为质因子的数
}
}
}
😀欧拉筛欧拉值
利用了欧拉筛的思想
避免重复筛的情况
节省了时间
const int maxn;
bool isprime[maxn];//isprime[i]表示i是否为质数
int prime[maxn];//prime[i]表示第i个质数的值
int phi[maxn];//欧拉值
int cnt = 0;
inline void GET_PHI(){
phi[1] = 1;
for(int i = 2; i <= maxn; i ++){
if(!isprime[i]) prime[++cnt] = i, phi[i] = i - 1;
for(int j = 1; j <= cnt && i * prime[j] <= maxn; j ++){
isprime[i * prime[j]] = 1;
if(i % prime[j] == 0){
phi[i * prime[j]] = phi[i] * prime[j];//定理:对于i % j == 0,有phi[i * j] = phi[i] * j
break;
}else phi[i * prime[j]] = phi[i] * (prime[j] - 1);//积性函数:如果gcd(i, j) == 1, phi[i * j] = phi[i] * phi[j]。在这里j为质数,所以有phi[i] * phi[j] = phi[i] * (j - 1)
}
}
}
📕例题
🐎仪仗队
洛谷《仪仗队》传送门
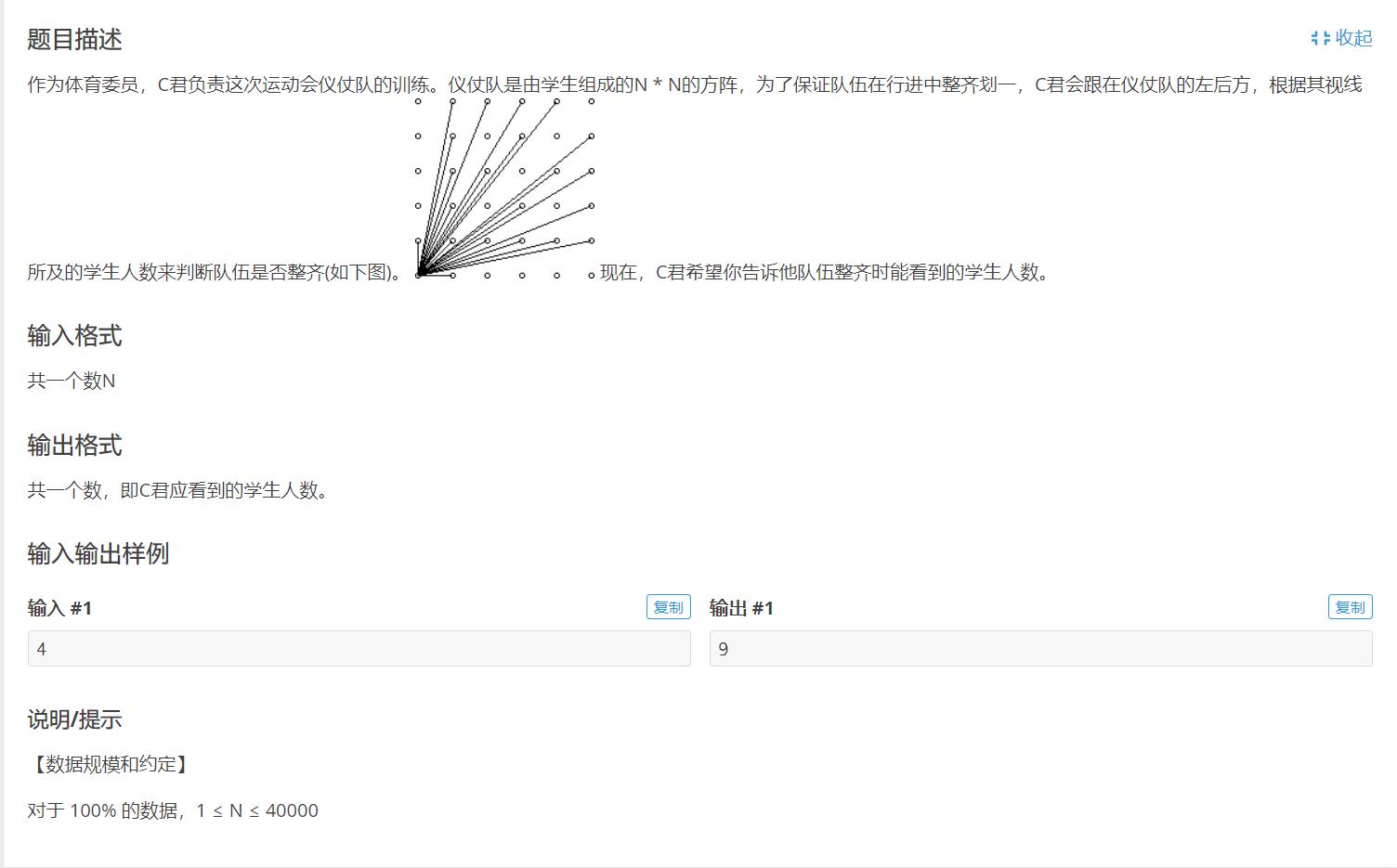
思路:
这道题我们可以将一个正方形沿对角线拆分成两部分
然后每一个能被看到的点一定是gcd(x, y) = 1的点
对每一行进行分析
在对角线内,gcd = 1的点也就是当前行数的欧拉值
所以我们在不计算(1, 1)的情况下
在一个三角形内,累加行数的欧拉值
再乘二得到两个三角形的欧拉值,再加上(1, 1)这个点即可
暴力计算代码
/*
________ _ ________ _
/ ______| | | | __ | | |
/ / | | | |__| | | |
| | | |___ _ _ _ ___ _ _____ | ___| ______ _____ ___ _ | |
| | | __ \\ |_| | | | | | _\\| | | ____| | |\\ \\ | __ | | _ | | _\\| | | |
| | | | \\ | _ | | | | | | \\ | | \\___ | | \\ \\ | |_/ _| | |_| | | | \\ | | |
\\ \\______ | | | | | | \\ |_| / | |_/ | ___/ | | | \\ \\ | /_ \\__ | | |_/ | | |
Author : \\________| |_| |_| |_| \\___/ |___/|_| |_____| _________|__| \\__\\ |______| | | |___/|_| |_|
____| |
\\_____/
*/
//#include <unordered_map>
#include <algorithm>
#include <iostream>
#include <cstring>
#include <string>
#include <vector>
#include <cstdio>
#include <stack>
#include <queue>
#include <cmath>
#include <utility>
#include <map>
#include <set>
#define G 10.0
#define LNF 1e18
#define EPS 1e-6
#define PI acos(-1.0)
#define INF 0x7FFFFFFF
#define ll long long
#define ull unsigned long long
#define LOWBIT(x) ((x) & (-x))
#define LOWBD(a, x) lower_bound(a.begin(), a.end(), x) - a.begin()
#define UPPBD(a, x) upper_bound(a.begin(), a.end(), x) - a.begin()
#define TEST(a) cout << "---------" << a << "---------" << '\\n'
#define CHIVAS int main()
#define _REGAL exit(0)
#define SP system("pause")
#define IOS ios::sync_with_stdio(false)
//#define map unordered_map
#define PB(x) push_back(x)
#define ALL(a) ((a).begin(),(a).end())
#define MEM(a, b) memset(a, b, sizeof(a))
#define EACH_CASE(cass) for (scanf("%d", &cass); cass; cass--)
#define LS l, mid, rt << 1
#define RS mid + 1, r, rt << 1 | 1
#define GETMID (l + r) >> 1
using namespace std;
template<typename T> inline T MAX(T a, T b){return a > b? a : b;}
template<typename T> inline T MIN(T a, T b){return a > b? b : a;}
template<typename T> inline void SWAP(T &a, T &b){T tp = a; a = b; b = tp;}
template<typename T> inline T GCD(T a, T b){return b > 0? gcd(b, a % b) : a;}
template<typename T> inline void ADD_TO_VEC_int(T &n, vector<T> &vec){vec.clear(); cin >> n; for(int i = 0; i < n; i ++){T x; cin >> x, vec.PB(x);}}
template<typename T> inline pair<T, T> MaxInVector_ll(vector<T> vec){T MaxVal = -LNF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal < vec[i]) MaxVal = vec[i], MaxId = i; return {MaxVal, MaxId};}
template<typename T> inline pair<T, T> MinInVector_ll(vector<T> vec){T MinVal = LNF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i]) MinVal = vec[i], MinId = i; return {MinVal, MinId};}
template<typename T> inline pair<T, T> MaxInVector_int(vector<T> vec){T MaxVal = -INF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal < vec[i]) MaxVal = vec[i], MaxId = i; return {MaxVal, MaxId};}
template<typename T> inline pair<T, T> MinInVector_int(vector<T> vec){T MinVal = INF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i]) MinVal = vec[i], MinId = i; return {MinVal, MinId};}
//template<typename T> inline pair<map<T, T>, vector<T> > DIV(T n){T nn = n;map<T, T> cnt;vector<T> div;for(ll i = 2; i * i <= nn; i ++){while(n % i == 0){if(!cnt[i]) div.push_back(i);cnt[i] ++;n /= i;}}if(n != 1){if(!cnt[n]) div.push_back(n);cnt[n] ++;n /= n;}return {cnt, div};}
inline int PHI(int n){
int res = n;
for(int i = 2; i * i <= n; i ++){
if(n % i == 0){
res = res * (i - 1) / i;
while(n % i == 0) n /= i;
}
}
if(n > 1) res = res * (n - 1) / n;
return res;
}
CHIVAS{
int n;
cin >> n;
if(n == 1){
cout << 0 << endl;
return 0;
}
int res = 0;
for(int i = 2; i < n; i ++) res += PHI(i);
cout << res * 2 + 3 << endl;
_REGAL;
}
埃氏筛欧拉值代码
/*
________ _ ________ _
/ ______| | | | __ | | |
/ / | | | |__| | | |
| | | |___ _ _ _ ___ _ _____ | ___| ______ _____ ___ _ | |
| | | __ \\ |_| | | | | | _\\| | | ____| | |\\ \\ | __ | | _ | | _\\| | | |
| | | | \\ | _ | | | | | | \\ | | \\___ | | \\ \\ | |_/ _| | |_| | | | \\ | | |
\\ \\______ | | | | | | \\ |_| / | |_/ | ___/ | | | \\ \\ | /_ \\__ | | |_/ | | |
Author : \\________| |_| |_| |_| \\___/ |___/|_| |_____| _________|__| \\__\\ |______| | | |___/|_| |_|
____| |
\\_____/
*/
//#include <unordered_map>
#include <algorithm>
#include <iostream>
#include <cstring>
#include <string>
#include <vector>
#include <cstdio>
#include <stack>
#include <queue>
#include <cmath>
#include <utility>
#include <map>
#include <set>
#define G 10.0
#define LNF 1e18
#define EPS 1e-6
#define PI acos(-1.0)
#define INF 0x7FFFFFFF
#define ll long long
#define ull unsigned long long
#define LOWBIT(x) ((x) & (-x))
#define LOWBD(a, x) lower_bound(a.begin(), a.end(), x) - a.begin()
#define UPPBD(a, x) upper_bound(a.begin(), a.end(), x) - a.begin()
#define TEST(a) cout << "---------" << a << "---------" << '\\n'
#define CHIVAS int main()
#define _REGAL exit(0)
#define SP system("pause")
#define IOS ios::sync_with_stdio(false)
//#define map unordered_map
#define PB(x) push_back(x)
#define ALL(a) ((a).begin(),(a).end())
#define MEM(a, b) memset(a, b, sizeof(a))
#define EACH_CASE(cass) for (scanf("%d", &cass); cass; cass--)
#define LS l, mid, rt << 1
#define RS mid + 1, r, rt << 1 | 1
#define GETMID (l + r) >> 1
using namespace std;
template<typename T> inline T MAX(T a, T b){return a > b? a : b;}
template<typename T> inline T MIN(T a, T b){return a > b? b : a;}
template<typename T> inline void SWAP(T &a, T &b){T tp = a; a = b; b = tp;}
template<typename T> inline T GCD(T a, T b){return b > 0? gcd(b, a % b) : a;}
template<typename T> inline void ADD_TO_VEC_int(T &n, vector<T> &vec){vec.clear(); cin >> n; for(int i = 0; i < n; i ++){T x; cin >> x, vec.PB(x);}}
template<typename T> inline pair<T, T> MaxInVector_ll(vector<T> vec){T MaxVal = -LNF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal < vec[i]) MaxVal = vec[i], MaxId = i; return {MaxVal, MaxId};}
template<typename T> inline pair<T, T> MinInVector_ll(vector<T> vec){T MinVal = LNF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i]) MinVal = vec[i], MinId = i; return {MinVal, MinId};}
template<typename T> inline pair<T, T> MaxInVector_int(vector<T> vec){T MaxVal = -INF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal < vec[i]) MaxVal = vec[i], MaxId = i; return {MaxVal, MaxId};}
template<typename T> inline pair<T, T> MinInVector_int(vector<T> vec){T MinVal = INF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i]) MinVal = vec[i], MinId = i; return {MinVal, MinId};}
//template<typename T> inline pair<map<T, T>, vector<T> > DIV(T n){T nn = n;map<T, T> cnt;vector<T> div;for(ll i = 2; i * i <= nn; i ++){while(n % i == 0){if(!cnt[i]) div.push_back(i);cnt[i] ++;n /= i;}}if(n != 1){if(!cnt[n]) div.push_back(n);cnt[n] ++;n /= n;}return {cnt, div};}
const int maxn = 400005;
int phi[maxn];
int n;
inline void GET_PHI(){
for(int i = 0; i <= n; i ++) phi[i] = i;
for(int i = 2; i <= n; i ++){
if(phi[i] == i){
for(int j = i; j <= n; j += i) phi[j] = phi欧拉函数及代码实现
hdu-2824 The Euler function(欧拉函数)