模式识别作业二 Fisher准则线性分类器设计

Posted 2021-05-16 鲁棒最小二乘支持向量机

【实验目的】

旨在让同学进一步了解分类器的设计概念，能够根据自己的设计对线性分类器有更深刻地认识，理解Fisher准则方法确定最佳线性分界面方法的原理，以及Lagrande乘子求解的原理。

【原理】

【作业内容】

已知有两类数据 和 , w1中数据点的坐标对应一一如下：

x1 =[0.2331 1.5207 0.6499 0.7757 1.0524 1.1974
0.2908 0.2518 0.6682 0.5622 0.9023 0.1333
-0.5431 0.9407 -0.2126 0.0507 -0.0810 0.7315
0.3345 1.0650 -0.0247 0.1043 0.3122 0.6655
0.5838 1.1653 1.2653 0.8137 -0.3399 0.5152
0.7226 -0.2015 0.4070 -0.1717 -1.0573 -0.2099];
x2 =[2.3385 2.1946 1.6730 1.6365 1.7844 2.0155
2.0681 2.1213 2.4797 1.5118 1.9692 1.8340
1.8704 2.2948 1.7714 2.3939 1.5648 1.9329
2.2027 2.4568 1.7523 1.6991 2.4883 1.7259
2.0466 2.0226 2.3757 1.7987 2.0828 2.0798
1.9449 2.3801 2.2373 2.1614 1.9235 2.2604];
x3 =[0.5338 0.8514 1.0831 0.4164 1.1176 0.5536
0.6071 0.4439 0.4928 0.5901 1.0927 1.0756
1.0072 0.4272 0.4353 0.9869 0.4841 1.0992
1.0299 0.7127 1.0124 0.4576 0.8544 1.1275
0.7705 0.4129 1.0085 0.7676 0.8418 0.8784
0.9751 0.7840 0.4158 1.0315 0.7533 0.9548];

w2 中数据点的坐标对应一一如下：

x4 =[1.4010 1.2301 2.0814 1.1655 1.3740 1.1829
1.7632 1.9739 2.4152 2.5890 2.8472 1.9539
1.2500 1.2864 1.2614 2.0071 2.1831 1.7909
1.3322 1.1466 1.7087 1.5920 2.9353 1.4664
2.9313 1.8349 1.8340 2.5096 2.7198 2.3148
2.0353 2.6030 1.2327 2.1465 1.5673 2.9414];

x5 =[1.0298 0.9611 0.9154 1.4901 0.8200 0.9399
1.1405 1.0678 0.8050 1.2889 1.4601 1.4334
0.7091 1.2942 1.3744 0.9387 1.2266 1.1833
0.8798 0.5592 0.5150 0.9983 0.9120 0.7126
1.2833 1.1029 1.2680 0.7140 1.2446 1.3392
1.1808 0.5503 1.4708 1.1435 0.7679 1.1288];
x6 =[0.6210 1.3656 0.5498 0.6708 0.8932 1.4342
0.9508 0.7324 0.5784 1.4943 1.0915 0.7644
1.2159 1.3049 1.1408 0.9398 0.6197 0.6603
1.3928 1.4084 0.6909 0.8400 0.5381 1.3729
0.7731 0.7319 1.3439 0.8142 0.9586 0.7379
0.7548 0.7393 0.6739 0.8651 1.3699 1.1458];

数据的样本点分布如下图：

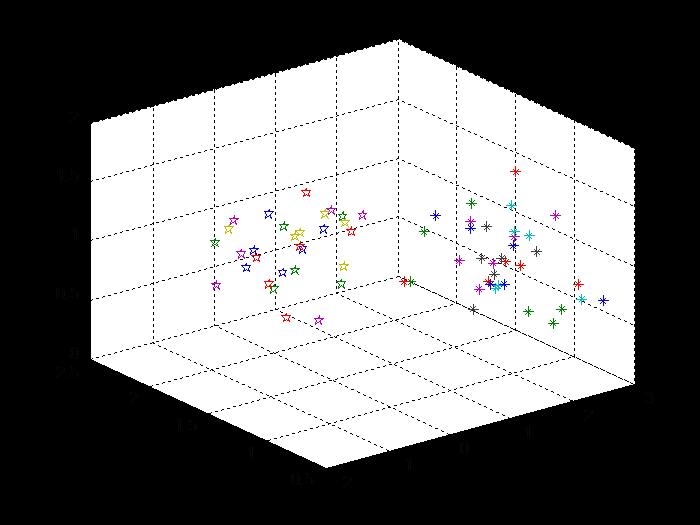
请把以上数据作为样本，设计Fisher分类器。

实验程序：

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

X1 = [0.2331,1.5207,0.6499,0.7757,1.0524,1.1974,
    0.2908,0.2518,0.6682,0.5622,0.9023,0.1333,
   -0.5431,0.9407,-0.2126,0.0507,-0.0810,0.7315,
    0.3345,1.0650,-0.0247,0.1043,0.3122,0.6655,
    0.5838,1.1653,1.2653,0.8137,-0.3399,0.5152,
    0.7226,-0.2015,0.4070,-0.1717,-1.0573,-0.2099]
X2 = [2.3385,2.1946,1.6730,1.6365,1.7844,2.0155,
    2.0681,2.1213,2.4797,1.5118,1.9692,1.8340,
    1.8704,2.2948,1.7714,2.3939,1.5648,1.9329,
    2.2027,2.4568,1.7523,1.6991,2.4883,1.7259,
    2.0466,2.0226,2.3757,1.7987,2.0828,2.0798,
    1.9449,2.3801,2.2373,2.1614,1.9235,2.2604]
X3 = [0.5338,0.8514,1.0831,0.4164,1.1176,0.5536,
    0.6071,0.4439,0.4928,0.5901,1.0927,1.0756,
    1.0072,0.4272,0.4353,0.9869,0.4841,1.0992,
    1.0299,0.7127,1.0124,0.4576,0.8544,1.1275,
    0.7705,0.4129,1.0085,0.7676,0.8418,0.8784,
    0.9751,0.7840,0.4158,1.0315,0.7533,0.9548]
X4 = [1.4010,1.2301,2.0814,1.1655,1.3740,1.1829,
    1.7632,1.9739,2.4152,2.5890,2.8472,1.9539,
    1.2500,1.2864,1.2614,2.0071,2.1831,1.7909,
    1.3322,1.1466,1.7087,1.5920,2.9353,1.4664,
    2.9313,1.8349,1.8340,2.5096,2.7198,2.3148,
    2.0353,2.6030,1.2327,2.1465,1.5673,2.9414]
X5 = [1.0298,0.9611,0.9154,1.4901,0.8200,0.9399,
    1.1405,1.0678,0.8050,1.2889,1.4601,1.4334,
    0.7091,1.2942,1.3744,0.9387,1.2266,1.1833,
    0.8798,0.5592,0.5150,0.9983,0.9120,0.7126,
    1.2833,1.1029,1.2680,0.7140,1.2446,1.3392,
    1.1808,0.5503,1.4708,1.1435,0.7679,1.1288]
X6 = [0.6210,1.3656,0.5498,0.6708,0.8932,1.4342,
    0.9508,0.7324,0.5784,1.4943,1.0915,0.7644,
    1.2159,1.3049,1.1408,0.9398,0.6197,0.6603,
    1.3928,1.4084,0.6909,0.8400,0.5381,1.3729,
    0.7731,0.7319,1.3439,0.8142,0.9586,0.7379,
    0.7548,0.7393,0.6739,0.8651,1.3699,1.1458]
# print(X1) 
x1 = np.array(X1)
# print(x1)
# x1 = x1.reshape((-1,1)) # 将X1变为列向量
# print(x1)
x2 = np.array(X2)
# x2 = x2.reshape((-1,1)) 
x3 = np.array(X3)
# x3 = x3.reshape((-1,1)) 
X = np.array([x1,x2,x3]) # (3,36)
# print(X)
XM = np.mean(X.T,axis=0) # 第一类的样本均值向量 (1,3)
# print(XM)
# 获取向量长度
lx1 = len(x1)
# print(lx1)
x4 = np.array(X4)
x5 = np.array(X5)
x6 = np.array(X6)
Y = np.array([x4,x5,x6]) # (3,36)
YM = np.mean(Y.T,axis=0) # 第二类的样本均值向量 (1,3)
# print(YM)
# 计算类样本类内离散度矩阵s1,s2 (3,3)
s1 = np.zeros((3,3))
s2 = np.zeros((3,3))
for i in range(lx1):
    a = X[:,i]-XM
    a = np.array([a])
    b = a.T
    s1 = s1 + np.dot(b,a)
# print(s1)
for i in range(lx1):
    a = Y[:,i]-YM
    a = np.array([a])
    b = a.T
    s2 = s2 + np.dot(b,a)
#print(s2)
sw = s1 + s2 # 总类内离散度矩阵sw (3,3)
print('总类内离散度矩阵:',sw)
m = np.array([XM-YM])
sb = np.dot(m.T,m) # 样本类间离散度矩阵sb (3,3)
print('样本类间离散度矩阵:',sb)
n =np.linalg.inv(sw)
W = np.dot(n,m.T) # 最优解W
print('最优解W:',W)
T = -0.5*(np.dot(np.dot((XM+YM),np.linalg.inv(sw)),m.T)) #阈值T
print('阈值T:',T)
plt.rcParams["font.family"] = "SimHei" # 添加了这句话可在图中显示中文
plt.rcParams["axes.unicode_minus"] = False # 添加了这一行使得负号可以显示
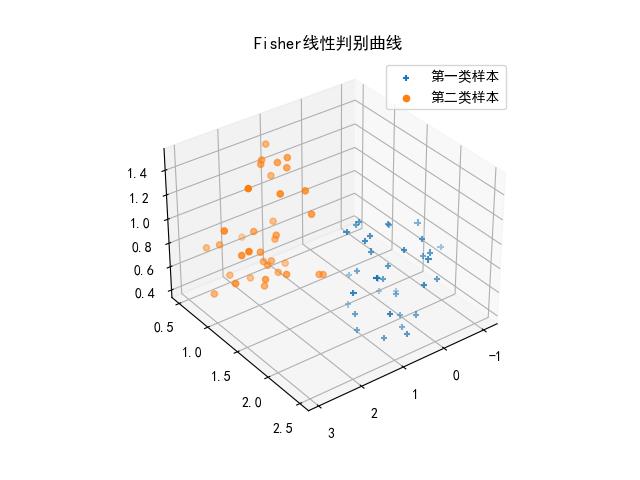
ax1 = plt.axes(projection='3d')
ax1.scatter3D(X1,X2,X3,marker='+',label='第一类样本')
ax1.scatter3D(X4,X5,X6,marker='o',label='第二类样本')
plt.title('Fisher线性判别曲线')
plt.legend()
plt.show()

实验结果：

本人能力有限，解释尚不清楚明了，如遇任何问题，大家可留言或私信。开源Matlab程序较多，大家按需参考学习使用。

本文希望对大家有帮助，当然上文若有不妥之处，欢迎指正。

分享决定高度，学习拉开差距