回溯算法之N皇后问题

Posted 2021-05-16 快乐江湖

解法框架

【README】回溯算法基本框架

全排列问题(点击跳转)

N皇后可谓是一个经典的问题

N皇后问题：在国际象棋棋盘，即8*8的棋盘上放8个“皇后”，保证它们之间不能互相攻击，换言之，任意两后不能位于棋盘的同一行、同一列或同一对角线上，满足条件的放法有多少种？

对于这道题，首先你要搞清楚是怎样下棋的。我们放置时，是从第一行开始的，放置结束后，放置下一个时，一定要从下一行开始，不能跳着行去放。所以选择列表是下一行的每一列，因为每一列都可以是一种选择的可能，不合理的可能就是，下一行的某一列放置后导致了皇后攻击

举个例子，第一次放置在了第一行的第一列，那么根据规则，下一行放置时只能放置在这些位置

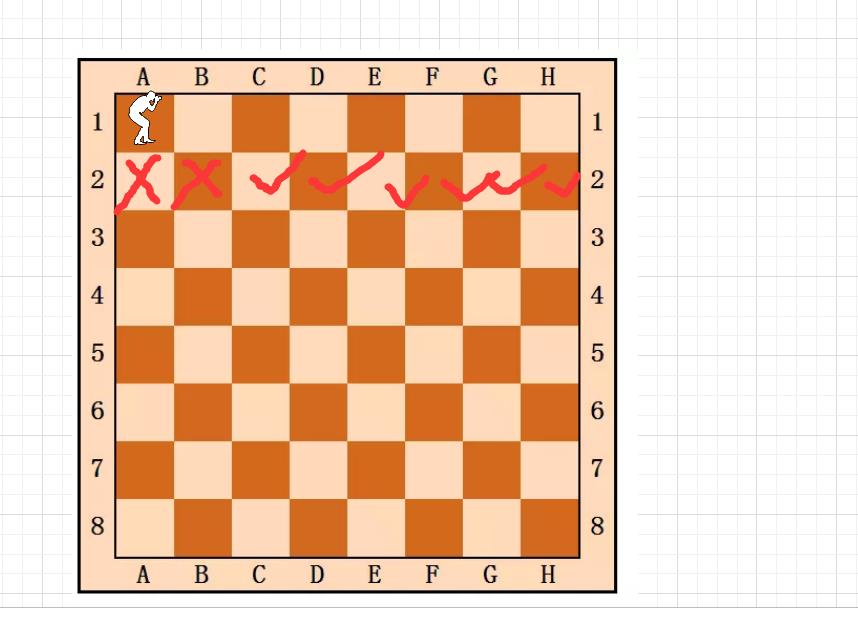
所以这道题和上一题的电话号码的组合有点相似，它的选择列表并不像全排列一样简单直白的给出来，而是有一种对应关系。在上一题中是，数字对应的是字母列表，而这一题则是每一行对应的列。

因此，首先摆出回溯算法基本框架

• 特别注意C++这种初始化棋盘的方式，n×n棋盘，n行，每一行都是一个有n个字符的字符串，字符.表示没有下棋，字符Q表示放置了一个皇后

对于选择列表则是每一行对应的列，所以就像电话号码的组合中键盘数字与字母的对应。因此使用一个变量row记录行号，每次进入back函数，都要在row+1，也就是下一行的所有列中选择合适的情况

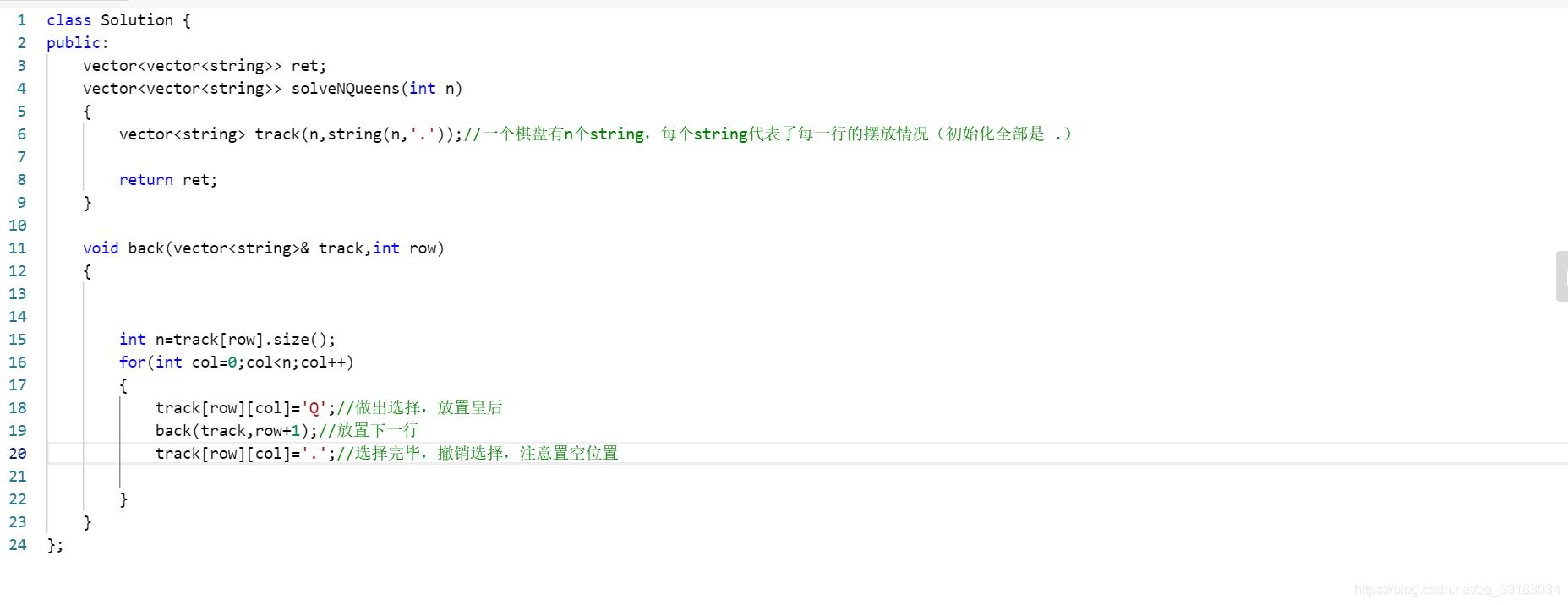
最后，最重要的也就是如何做出正确的选择——不要使得皇后互相攻击。

即：每次放置皇后时，都要保证以它为中心的上下左右，左上左下，右上右下射线方向均不出现皇后，所以我们要定义一个判断规则的函数。对于这个函数不用每个方向都去判断，我们只需判断左上，右上和正上方即可。因为放置时是每一行只能放置一个，所以它的左右不可能有皇后，又因为放置时是放置在上一个放置了皇后的行的下一行，所以不可能跳跃的下一行放置，也就是正下方，左下，右下均不会出现皇后

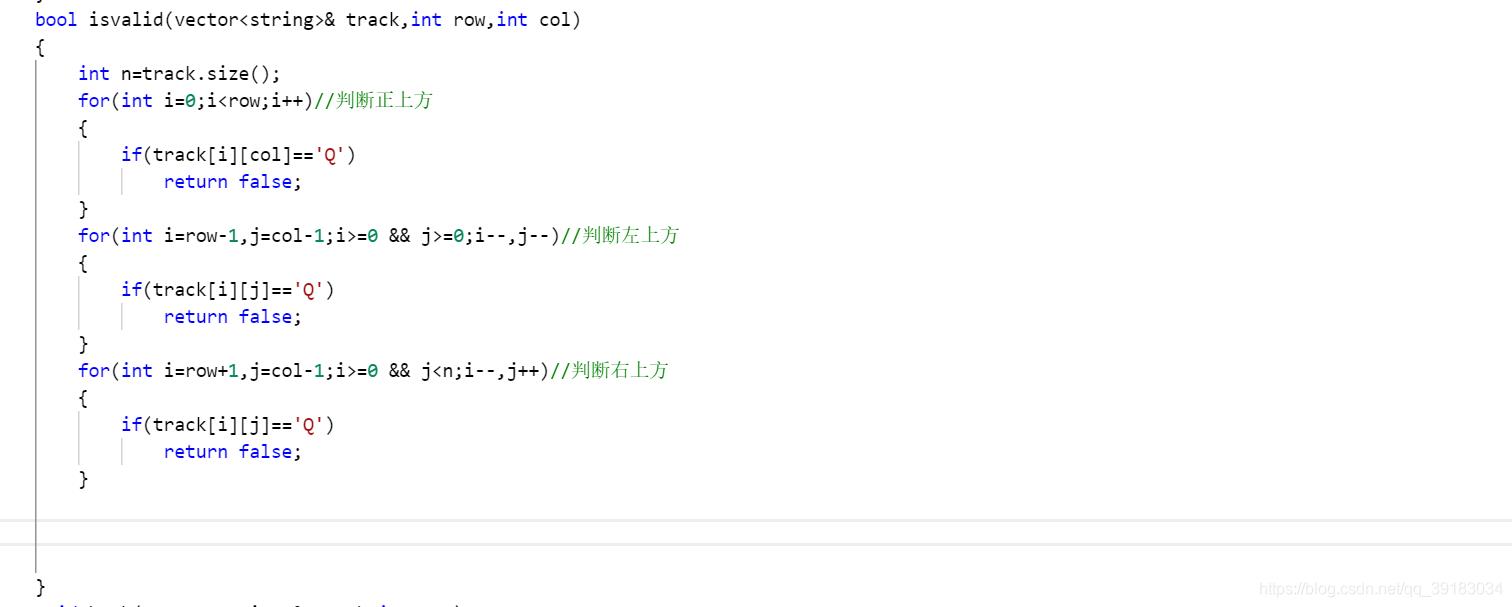
最后就是结束条件，也就是如果把最后一行也放了，那么就代表一种正确的情况，因此加入到返回结果中

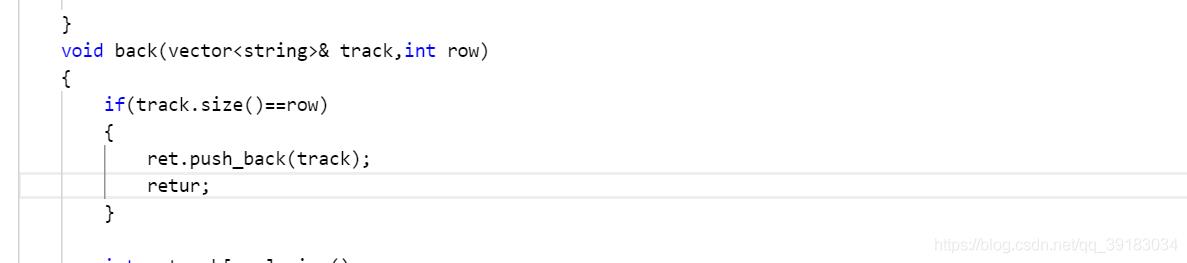
代码如下

class Solution {
public:
    vector<vector<string>> ret;//结果
    vector<vector<string>> solveNQueens(int n) 
    {
        vector<string> track(n,string(n,'.'));//跟踪（棋盘n×n列，“.”表示空）
        back(track,0);
        return ret;
    }
    void back(vector<string>& track,int row)//回溯函数
    {
        if(row==track.size())
        {
            ret.push_back(track);
            return;
        }

        int n=track[row].size();
        for(int col=0;col<n;col++)
        {
            if(!isvalid(track,row,col))
                continue;
            track[row][col]='Q';
            back(track,row+1);
            track[row][col]='.';

        }
    }

    bool isvalid(vector<string>& track,int row,int col)
    {
        /*放置皇后时，是在下一列放置的，所以只需检测*/
        int n=track.size();
        for(int i=0;i<row;i++)
        {
            if(track[i][col]=='Q')
                return  false;
        }
        for(int i=row-1,j=col+1;i>=0 && j<n;i--,j++)
        {
            if(track[i][j]=='Q')
                return  false;
        }
        for(int i=row-1,j=col-1;i>=0 && j>=0;i--,j--)
        {
            if(track[i][j]=='Q')
                return  false;
        }
        return true;


    }

};