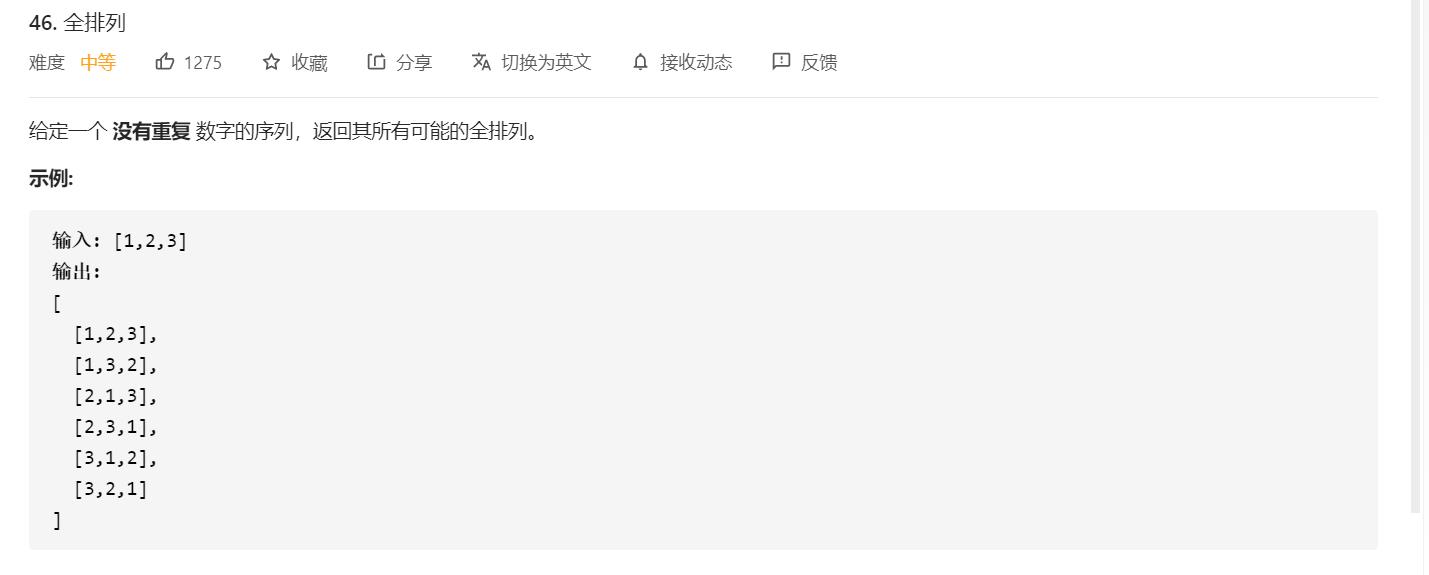
回溯算法之全排列问题

Posted 2021-05-16 快乐江湖

解法框架

【README】回溯算法基本框架

全排列问题(点击跳转)

首先我们需要仔细观察函数的返回值和形参等（这里我使用的C++，因为它处理数组，字符串特别方便），这里形参是一个vector的引用，也就是一个数组，那么它肯定可以作为选择列表，返回值则是一个二维数组，二维数组中每一个元素保存的是一个正确的返回结果

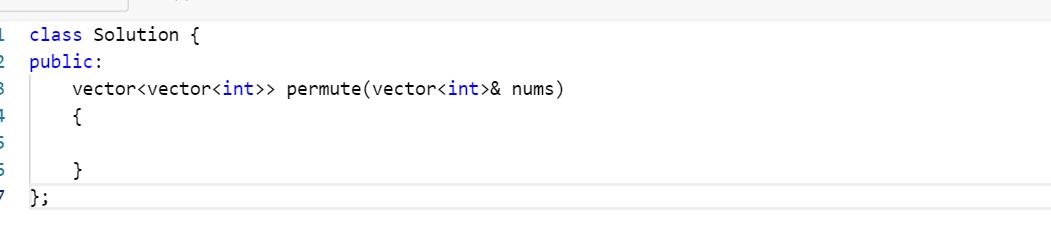
那么这里我们就对应起来了，返回是二维数组，二维数组中的每项都是一个vector，所以咋们的路径也一定是一个vector，每次达到结束条件之后，把一个路径作为二维数组的一项添加进去。

于是在全局定义，二维数组，在函数内部定义路径

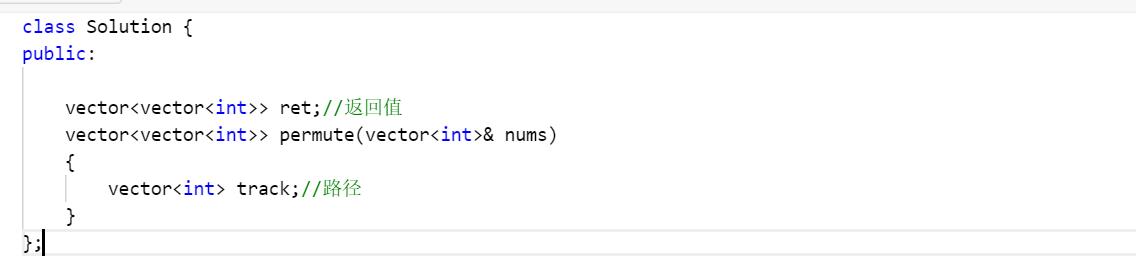
好的下一步就是回溯算法核心：遍历决策树
遍历一个决策树的递归函数backtrack，其形参分别是路径track和选择列表nums，
我们说过此函数内部就是做选择，递归，撤销选择循环过程。而做选择时候就是在遍历选择列表，于是我们可以写成这样

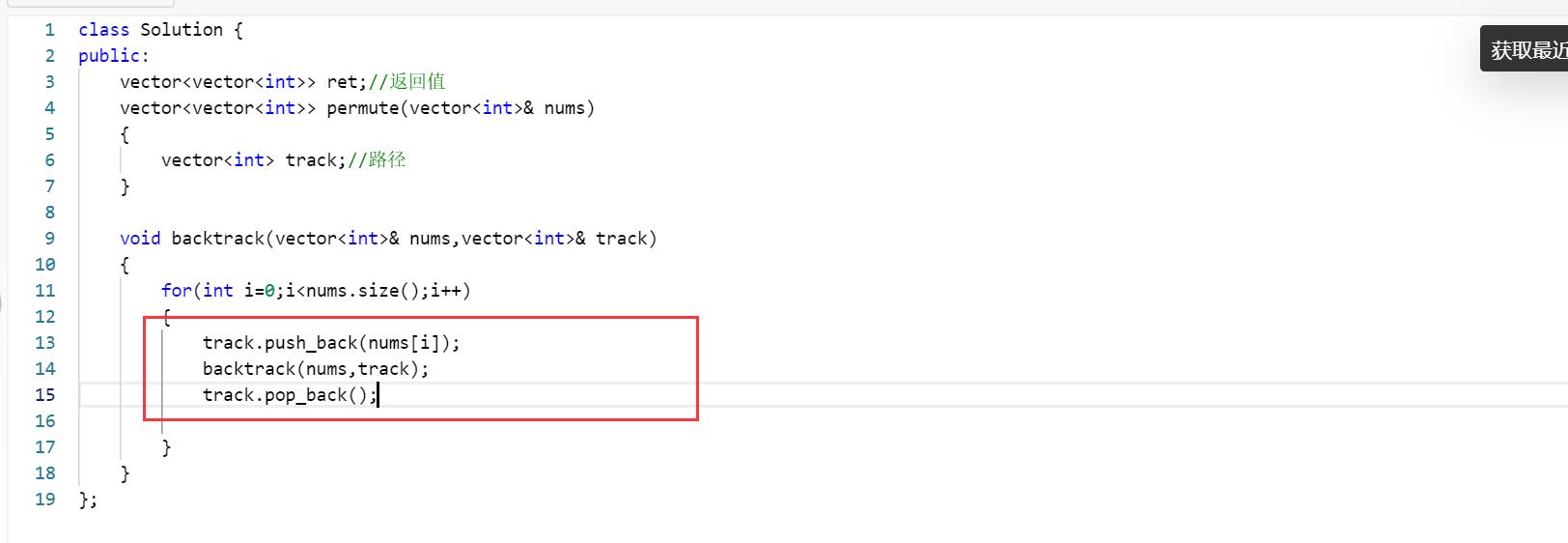
但是这样对吗，肯定是有问题的。前面我们说过，做选择要求的是做出正确的选择，而全排列要求数字全部不重复，所在做出选择之前，我们要进行判断，要是当前的选择已经出现过了那么就直接跳过。

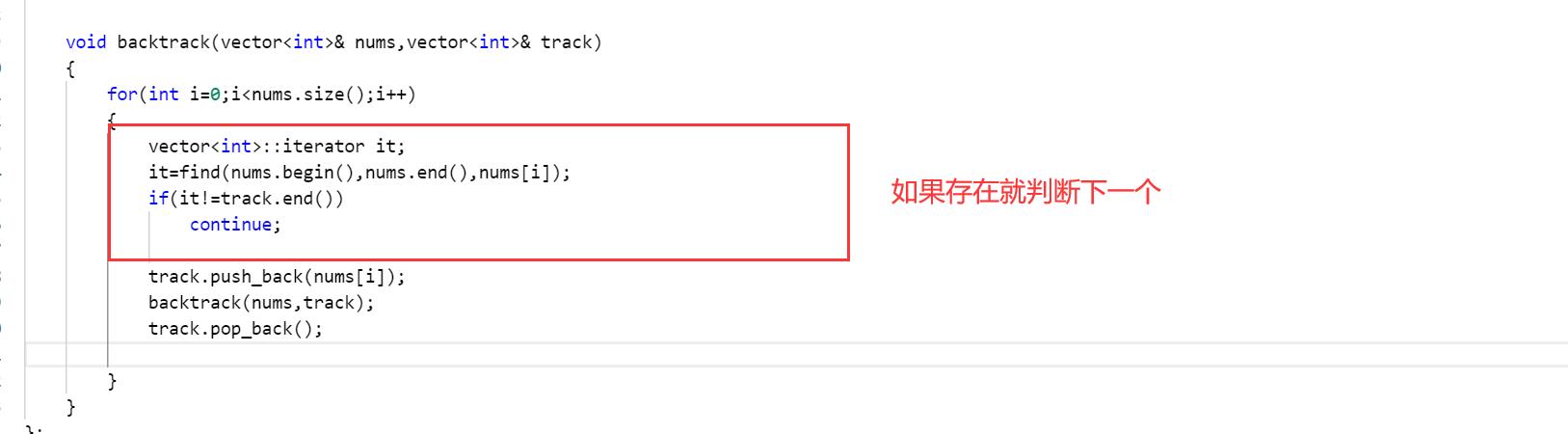
最后也是最为重要的，那就是一定要有结束条件，这里结束条件就是选够三个数字之后就可以结束了，选择够三个数字，此时的track就可以作为ret的一项被添加进去了

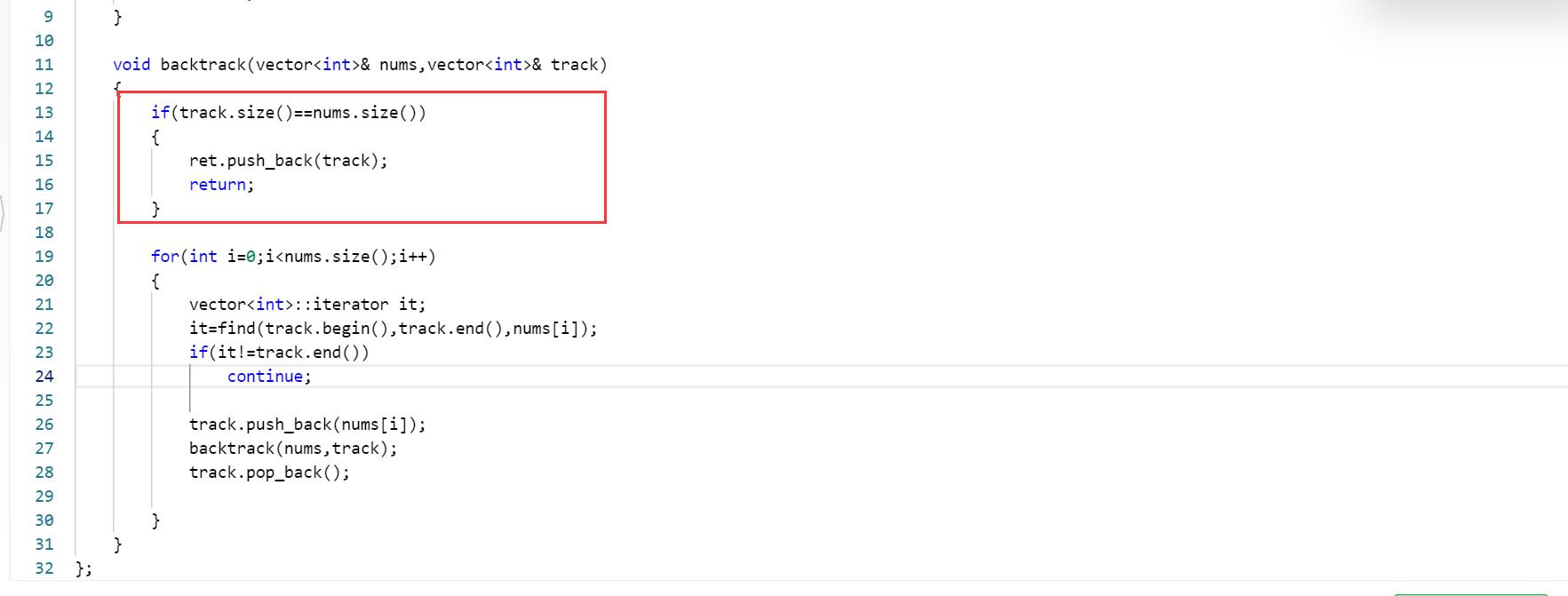
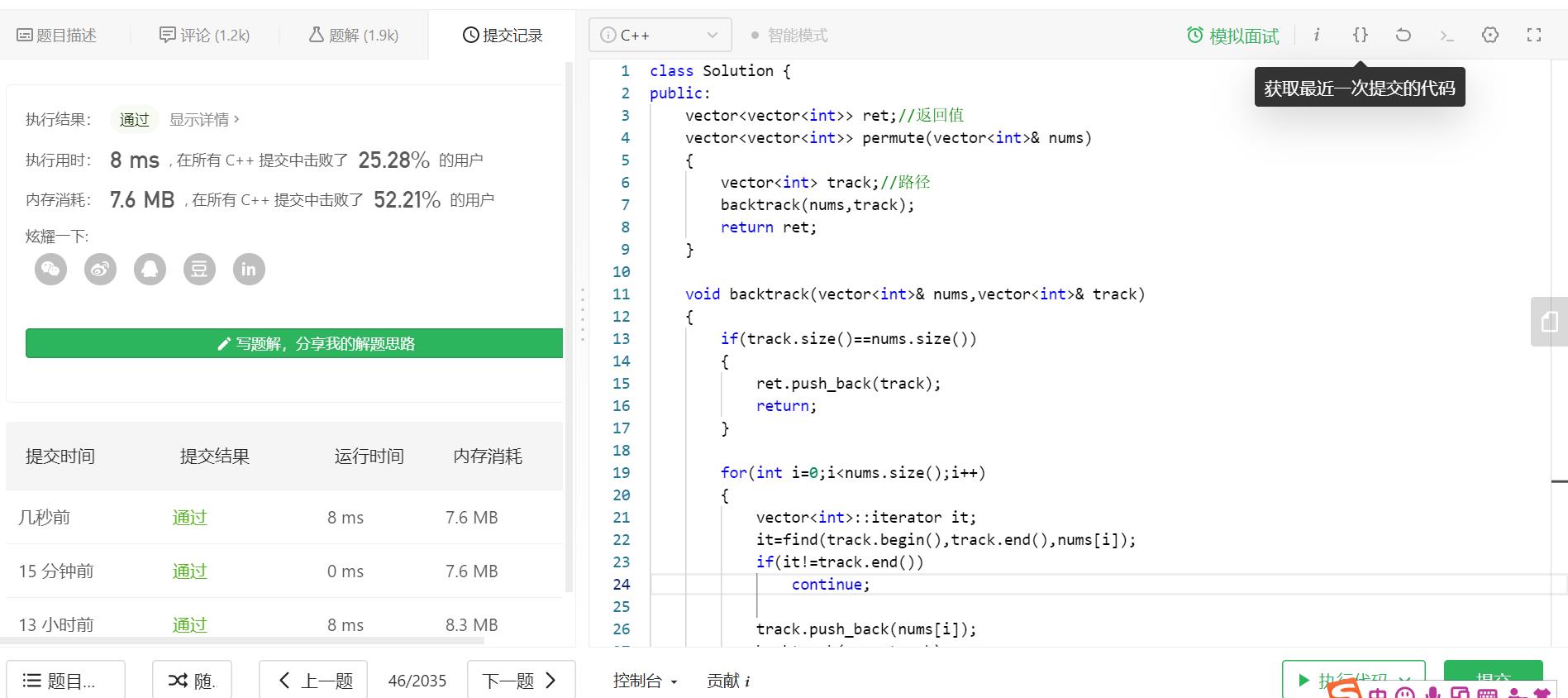
好的代码如下，这里还需要强调C++的一个问题呢，那个形参最好搞成引用，不然会引发很大拷贝，空间代价太高了

class Solution {
public:
    vector<vector<int>> ret;//返回

    vector<vector<int>> permute(vector<int>& nums)
    {
        vector<int> track;//路径
        backtrack(nums,track);//递归

        return ret;
    }

    void backtrack(vector<int>& nums,vector<int> track)
    {
        if(track.size()==nums.size())//达到结束条件，一个全排列生成
        {
            ret.push_back(track);//把一种结果添加进去
            return;

        }

        for(int i=0;i<nums.size();i++)
        {
            vector<int>::iterator it;//找一下nums[i]是否已经有了，有了的话直接接下一个
            it=find(track.begin(),track.end(),nums[i]);
            if(it!=track.end())
                continue;

            track.push_back(nums[i]);//做出选择
            backtrack(nums,track);//遍历决策树
            track.pop_back();//撤销选择
        }
    }
};