（LeetCode）Java 求解灌溉花园的最少水龙头数目

Posted 2021-05-16 南淮北安

文章目录

• • 一、题目
  • 二、题解
  • 三、总结

一、题目

在 x 轴上有一个一维的花园。花园长度为 n，从点 0 开始，到点 n 结束。

花园里总共有 n + 1 个水龙头，分别位于 [0, 1, ..., n] 。

给你一个整数 n 和一个长度为 n + 1 的整数数组 ranges ，其中 ranges[i] （下标从 0 开始）表示：如果打开点 i 处的水龙头，可以灌溉的区域为 [i - ranges[i], i + ranges[i]] 。

请你返回可以灌溉整个花园的最少水龙头数目 。

如果花园始终存在无法灌溉到的地方，请你返回 -1 。

示例1：

二、题解

该题属于一维的区间合并，具体的方法 起点合并，然后通过贪心的方法，进行具体分析：

（1）找到每个水龙头可以灌溉的左右位置
（2）对左位置排序
（3）初始，在所有小于等于0的左边界中找到右边界最大的位置节点
（4）然后把以右边界为哨兵位置，在左边界小于哨兵位置中寻找所有水龙头右边界最大的节点
（5）遍历过程中更新最大右边界即可

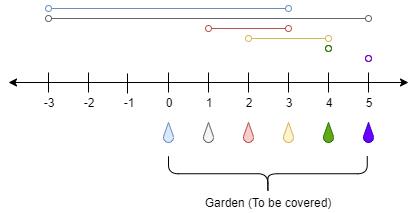
比如：n=7,ranges=[1,2,1,0,2,1,0,1]

（1）花园长度为7，一共,8个水龙头，灌溉的位置分别是：
[-1,1],[-1,3],[1,3],[3,3],[2,6],[4,6],[6,6],[6,8]
（2）对左位置排序：[-1,3],[-1,1],[1,3],[2,6],[3,3],[4,6],[6,8],[6,6]
（3）选择左位置最大的节点：[-1,3]
（4）以3为右边界，在左位置小于等于3的节点中选择右位置最大的节点，即在[-1,1],[1,3],[2,6],[3,3]
中选择，右位置最大的节点，即选择[2,6]
（5）然后以6为右边界，可供选择的有：[4,6],[6,8],[6,6]，选择[6,8]
（6）一共三个节点，选择结束

class Solution {
    public int minTaps(int n, int[] ranges) {
        //定义区间数组，存储每个水龙头的浇灌范围
        //region[i][0]表示第i个水龙头浇灌的左边界
        //region[i][1]表示第i个水龙头浇灌的右边界
        int[][] region = new int[n + 1][2];
        //将水龙头位置信息，转为洒水区间信息
        for (int i = 0; i < ranges.length; i++) {
            //存储左边界信息，最小为0
            region[i][0] = Math.max(0, i - ranges[i]);
            //存储右边界信息，最大为n
            region[i][1] = Math.min(n, i + ranges[i]);
        }
        //按照左边界排序，左边界相同的右边界大的排左边
        Arrays.sort(region, (a, b) -> a[0] == b[0] ? b[1] - a[1] : a[0] - b[0]);
        //记录需要的水龙头数目
        int num = 0;
        //记录哨兵位置，也就是右边界
        int right = 0;
        //遍历全部的水龙头
        int index = 0;
        while (index < n + 1) {
            //如果下一个水龙头的左边界大于此时的哨兵位置，说明区间不连贯，无法覆盖
            if (region[index][0] > right) {
                break;
            }
            int tempRight = right;
            //以右边界为哨兵，寻找左边界小于等于哨兵，但是右边界最大的节点
            while (index < n + 1 && region[index][0] <= right) {
                tempRight = Math.max(tempRight, region[index][1]);
                index++;
            }
            //重新记录哨兵
            right = tempRight;
            //记录数目加一
            num++;
            if (right == n) {
                break;
            }
        }
        return right == n ? num : -1;
    }
}

三、总结

所谓的贪心算法就是每次都找最优解，所以需要先进行排序，排序之后再具体分析

本题每个水龙头都有两个状态，左边界和右边界，所以需要定义int[][] region = new int[n + 1][2];

因为要排序，所以需用重新定义排序规则，如果左边界相同则按照右边界递减排序，左边界不同，则按照左边界递增排序

//按照左边界排序，左边界相同的右边界大的排左边
Arrays.sort(region, (a, b) -> a[0] == b[0] ? b[1] - a[1] : a[0] - b[0]);

接下来的，以找到的最大右边界为哨兵，继续进行遍历排序