《LeetCode之每日一题》:25. 不同路径

Posted 2021-05-16 是七喜呀！

不同路径

• 有关题目
• • 题解

题目链接： 不同路径

有关题目

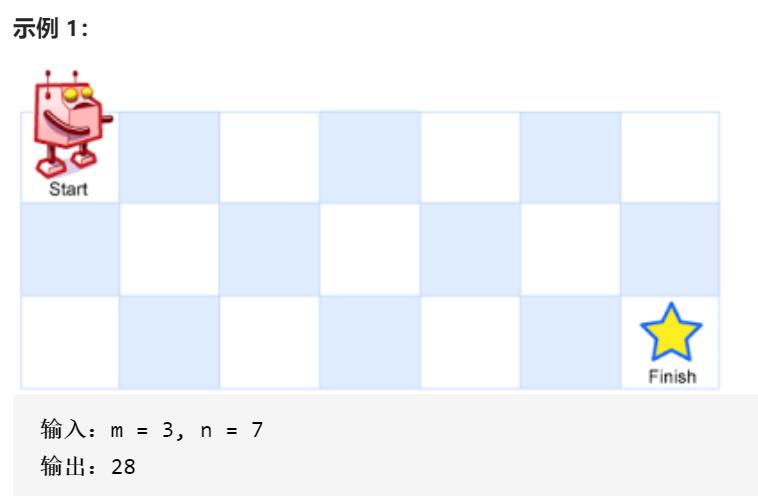
一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

示例 2：

输入：m = 3, n = 2
输出：3
解释：
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下

提示：

1 <= m, n <= 100
题目数据保证答案小于等于 2 * 10^9

题解

1、递归

static int a[101][101] = { 0 };//开辟最大的元素个数的数组,静态变量放在class外面（类似全局变量），并初始化。
class Solution {
public:
int uniquePaths(int m, int n) {
	
	if (m == 1 || n == 1)
		return 1;
	if (m == 2)
		return n;
	if (n == 2)
		return m;
	if (a[m][n] > 0)//计算过就直接返回。
		return a[m][n];
	a[m - 1][n] = uniquePaths(m - 1, n);
	a[n][m - 1] = a[m - 1][n];//由于本题的对称性，可以直接复制到对称位置
	a[m][n-1] = uniquePaths(m, n - 1);
	a[n - 1][m] = a[m][n - 1];//由于本题的对称性，可以直接复制到对称位置
	a[m][n] = a[m - 1][n] + a[m][n-1];
	return  a[m][n];//递归法
}
//注：这题较只递归要好很多，因为有用一个数组a记录下已经算过的路径数，避免了超时问题。
//假如a[7][3]时，有小伙伴可能有疑问，就是[3][6]又不存在，怎么得出结果？
//其实，我们在代码最上面开辟了存放最大数组元素的方阵就是为了解决这个问题的。由于对称性，虽然有些部分我们不需要，但是并不会影响我们的结果，例如：
//a[4][3]
// 1 1 1 1
// 1 2 3 4
// 1 3 6 10
// 1 4 10 20-->这边虽然我们有赋值，再对称性的条件下，不影响我们的结果，
};

2、动态规划

思路：
1、定义数组元素含义：dp[i][j]表示机器人位于矩阵(i,j)有dp[i][j]种路径
2、找出关系数组元素间的关系式：dp[i][j] = dp[i][j - 1] + dp[i - 1][j];
3、找出初始值：当机器人位于最上面一行只能往右走，即就一种走法.同理当机器人位于最左边一列时只能往下走，即就一种走法

int uniquePaths(int m, int n){
    int dp[m][n];
    memset(dp,0,sizeof(dp));
    //这边不需要判断 m == 1||n == 1时的走法，下面可以判断出只有一种走法
    for (int i = 0; i < m; i++)
    {
        dp[i][0] = 1;
    }
    for (int j = 0; j < n; j++)
    {
        dp[0][j] = 1;
    }
    for (int i = 1; i < m; i++)
    {
        for (int j = 1; j < n; j++)
        {
            dp[i][j] = dp[i][j - 1] + dp[i - 1][j];
        }
    }
    return dp[m - 1][n - 1];
}

时间复杂度：O(mn)
空间复杂度：O(mn)

C++版本

class Solution {
public:
    int uniquePaths(int m, int n) {
    vector<vector<int>> dp(m, vector<int>(n));
    for (int i = 0 ; i < m; i++)
    {
        dp[i][0] = 1;
    }
    for (int j = 0; j < n; j++)
    {
        dp[0][j] = 1;
    }
    for (int i = 1; i < m; i++)
    {
        for (int j = 1; j < n; j++)
        {
            dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
        }
    }
    return dp[m - 1][n - 1];
    }
};

时间复杂度：O(mn)
空间复杂度：O(mn)

3、滚动数组（内存优化）

思路：
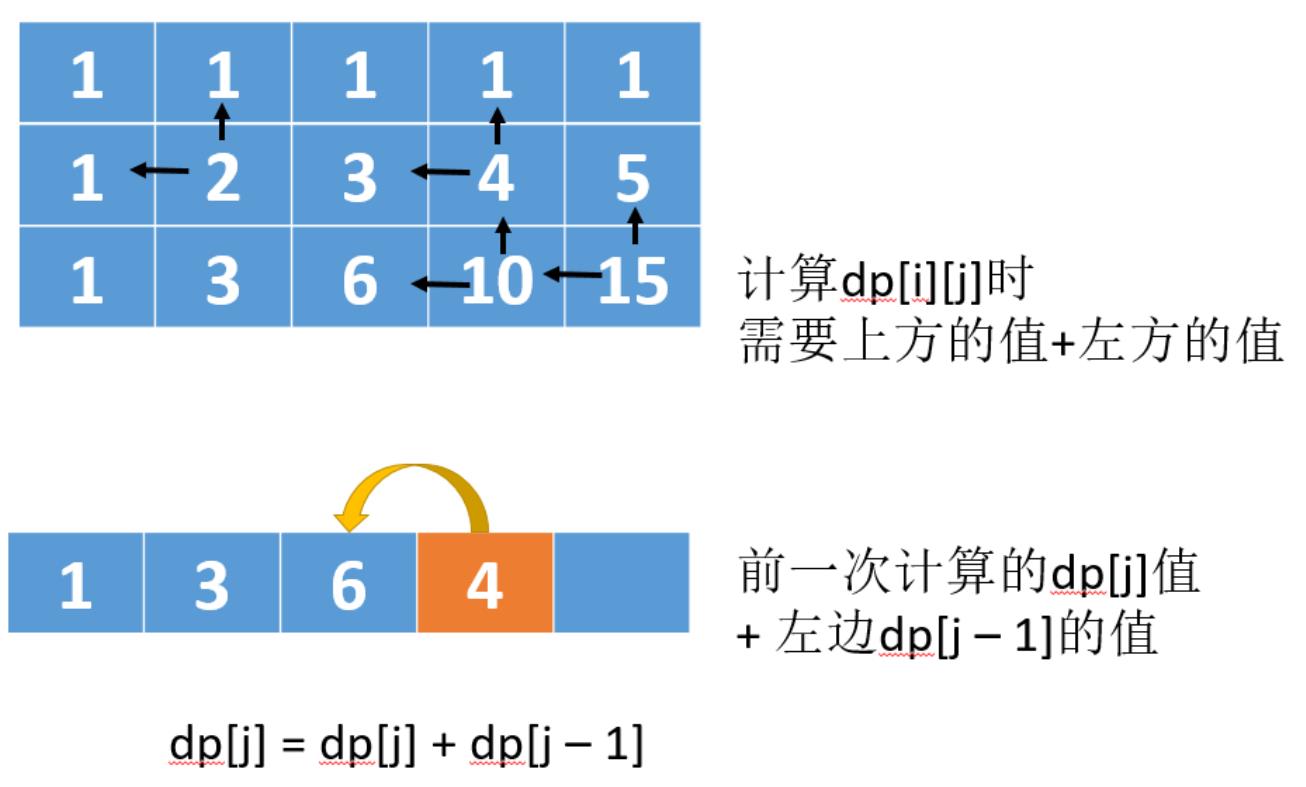
1、我们只需要上一行的值就可以了，上上一行的并不需要，所以这里可以用滚动数组的方式优化一下空间。
2、只用一个一维数组，滚动更新每行的路径数量
3、此时dp[j]含义为：第某行第j列的路径数量为dp[j]
4、转移方程：dp[j] = dp[j] + dp[j - 1]
第i行第j列位置的路径数量 = 第i - 1行第j列位置的路径数量 + 第i行第j - 1列位置的路径数量

参考链接：王尼玛

int uniquePaths(int m, int n){
    int dp[n];
    for (int i = 0; i < n; i++)
    {
        dp[i] = 1;//优化后的数组值，跟上图示，最上面的一行和最左边一列都是1，所以我们肯定从1开始进行滚动数组的优化。
    }
    for (int i = 1; i < m; i++)
    {
        for (int j = 1; j < n; j++)
        {
            dp[j] = dp[j - 1] + dp[j];
        }
    }
    return dp[n - 1];
}

时间复杂度：O(mn)
空间复杂度：O(n)

C++版本

class Solution {
public:
    int uniquePaths(int m, int n) {
    vector<int> dp(n,1); 
    for (int i = 1; i < m; i++)
    {
        for (int j = 1; j < n; j++)
        {
            dp[j] = dp[j] + dp[j - 1];//可简写dp[j] += dp[j - 1]
        }
    }
    return dp[n - 1];
    }
};

时间复杂度：O(mn)
空间复杂度：O(n)，
由于我们交换行列的值并不会对答案产生影响，因此我们总可以通过交换 m 和 n 使得 m小于等于n,这样空间复杂度降低至 O(min(m, n))。

4、数学法

思路：
从左上角到右下角的过程中，我们需要移动m + n - 2步，
其中m - 1步向下，n - 1步向右,故我们结合组合排序的知识有下图示

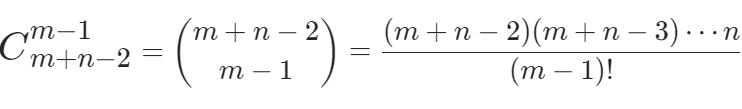
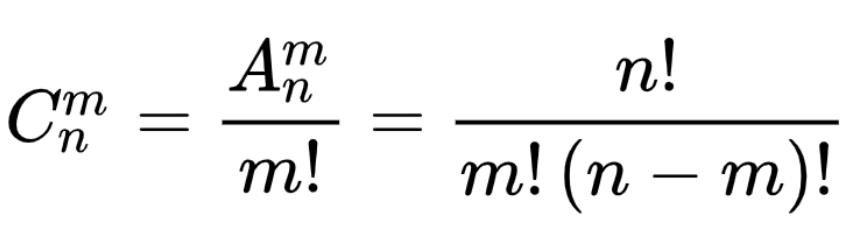
代码一：

class Solution {
public:
    int uniquePaths(int m, int n) {
        if (m > n)
            swap(m,n);//这边是为了保证能将空间复杂度优化而进行的交换
        int tmp = 1;
        long long int res = 1;
        for (int i = 2 ; i < m; i++)
            tmp *= i;
        for (int i = n; i < m + n - 1; i++)
            res *= i;
        return res / tmp;
    }
};

代码二：

class Solution {
public:
    int uniquePaths(int m, int n) {
    if ( m > n)
    	swap(m,n);
    long long res = 1;//注意哈，这边是啥类型
    for (int x = n, y = 1; y < m; x++,y++)
        res = res * x / y;
        return res;
    }
    
};

时间复杂度：O(m),我们在题干中保证了m <= n
空间复杂度：O(1)