《LeetCode之每日一题》:28. 最小路径和

Posted 2021-05-16 是七喜呀！

最小路径和

• 有关题目
• • 题解

题目链接： 最小路径和

有关题目

给定一个包含非负整数的 m x n 网格 grid 
请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

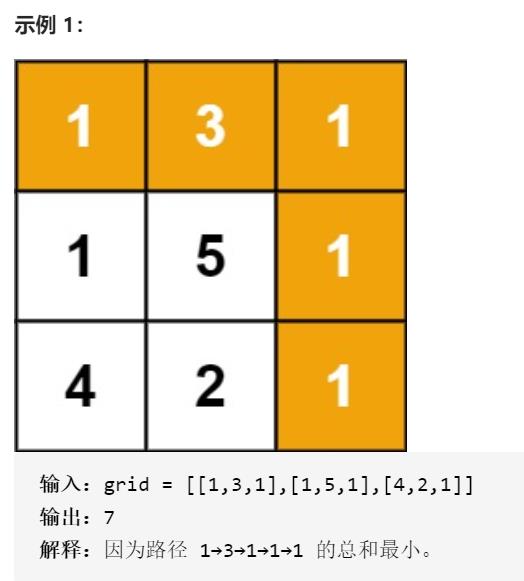
示例 2：

输入：grid = [[1,2,3],[4,5,6]]
输出：12

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 200
0 <= grid[i][j] <= 100

题解

1、动态规划

思路：
1.定义数组含义：(i,j)位置最小路径和为dp[i][j]
2.找出状态转移方程，即数组元素间的递推公式。
	分类讨论
3.找出初始值。第一行元素只能向右移动，第一列元素只能向下移动。处在初始位置时dp[0][0] = grid[0][0];

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        int m = grid.size();
        int n = grid[0].size();
        vector<vector<int>> dp(m,vector<int>(n));
        dp[0][0] = grid[0][0];
        for(int i = 1; i < m; i++)
        {
            dp[i][0] = dp[i - 1][0] + grid[i][0];
        }
        for (int j = 1; j < n; j++)
        {
            dp[0][j] = dp[0][j - 1] + grid[0][j];
        }
        for (int i = 1; i < m; i++)
        {
            for (int j = 1; j < n; j++)
            {
                dp[i][j] = min(dp[i - 1][j] , dp[i][j - 1]) + grid[i][j];
            }
        }
        return dp[m - 1][n - 1];
    }
};

时间复杂度：O(mn)
空间复杂度：O(mn)

2、滚动数组

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        int m = grid.size();
        int n = grid[0].size();
        vector<int> dp(n,INT_MAX);
        //不写INT_MAX也可以，因为dp[i]存放的是最小路径和，大小是根据dp[i]与dp[i - 1]变化的，即除了原数组全为0之外，这个数组最小路径和为0，其他情况是不可能的
        for (int i = 0; i < m; i++)
        {
            for (int j = 0; j < n; j++)
            {
                if (i == 0 && j == 0)
                    dp[0] = grid[0][0];
                else if (i == 0)//此时j != 0
                    dp[j] = dp[j - 1] + grid[0][j];
                else if (j == 0)
                    dp[j] = dp[j] + grid[i][0];//这能向上面一个元素获取值了
                else
                    dp[j] = min(dp[j],dp[j - 1]) + grid[i][j]; 
            }
        }
        return dp[n - 1];
    }
};

时间复杂度：O(mn)
空间复杂度：O(n)

3、O(1)空间复杂度

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        int m = grid.size();
        int n = grid[0].size();
        for (int i = 0 ; i < m; i++)
        {
            for (int j = 0; j < n; j++)
            {
                if (i == 0 && j == 0)
                    continue;
                else if (i == 0)
                    grid[i][j] = grid[i][j - 1] + grid[i][j];
                else if (j == 0)
                    grid[i][j] = grid[i - 1][j] + grid[i][j];
                else
                    grid[i][j] = min(grid[i - 1][j],grid[i][j - 1]) + grid[i][j];
            }
        }
    return grid[m - 1][n -1];
    }
};

时间复杂度：O(mn)
空间复杂度：O(1)