leetcode 面试题 17.16. 按摩师

Posted 2021-05-16 大忽悠爱忽悠

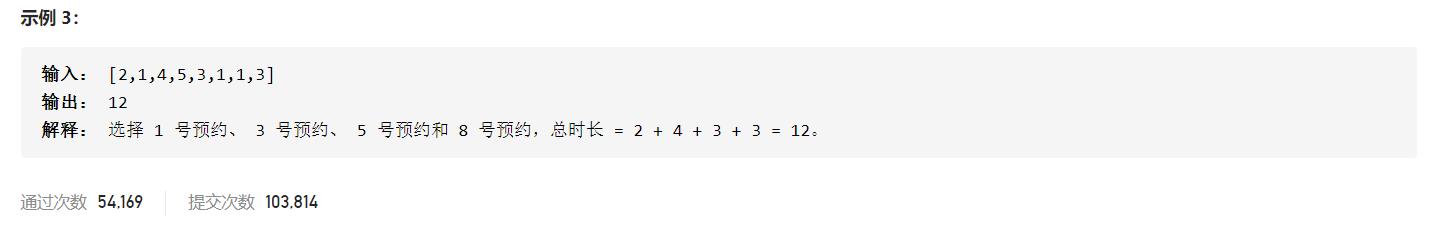
动态规划:

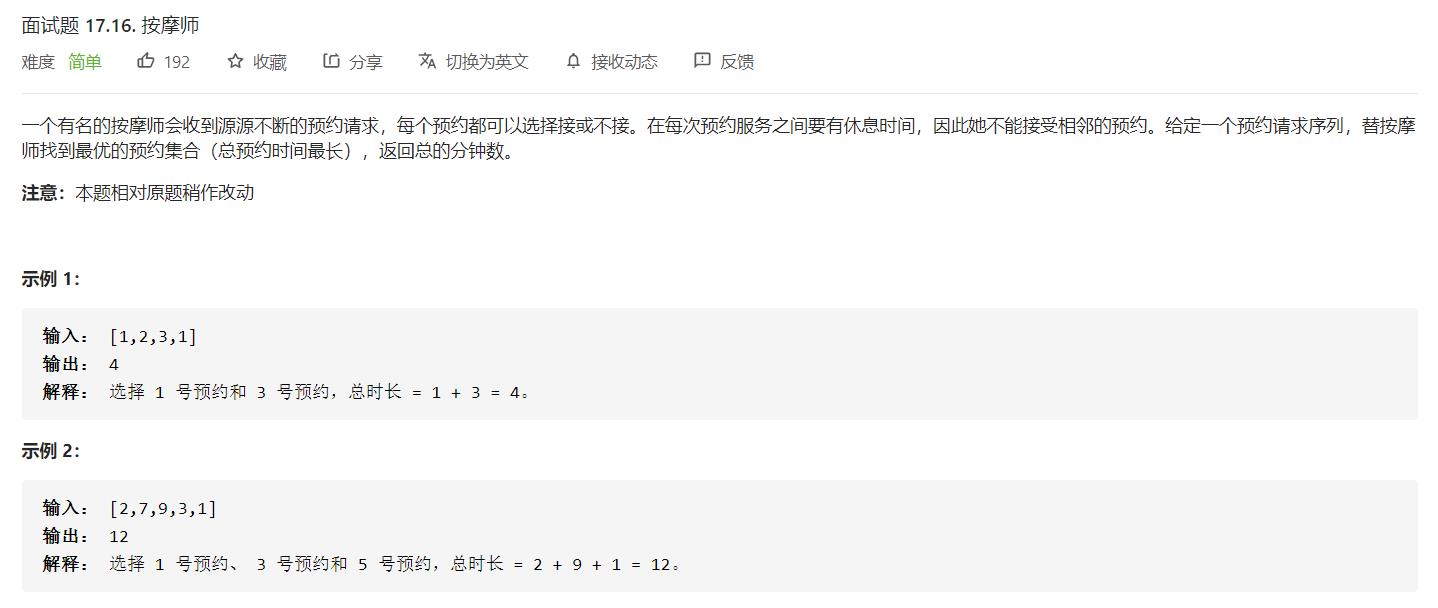
• 数组中的值表示的是预约时间，按摩师可以选择接或者不接，如果前一个接了，那么下一个肯定是不能接的，因为按摩师不能接相邻的两次预约。如果上一个没接，那么下一个可以选择接也可以选择不接，视情况而定。

• 这里可以定义一个二维数组dp[length][2]，其中dp[i][0]表示第i+1（因为数组下标是从0开始的，所以这里是i+1）个预约没有接的最长总预约时间，dp[i][1]表示的是第i+1个预约接了的最长总预约时间。那么我们找出递推公式

• 1，dp[i][0]=max(dp[i-1][0],dp[i-1][1])

• 他表示如果第i+1个没有接，那么第i个有没有接都是可以的，我们取最大值即可。

• 2，dp[i][1]=dp[i-1][0]+nums[i]

• 他表示的是如果第i+1个接了，那么第i个必须要没接，这里nums[i]表示的是第i+1个预约的时间。

• 递推公式找出来之后我们再来看下边界条件，第一个预约可以选择接，也可以选择不接，所以

• dp[0][0]=0，第一个没接

• dp[0][1]=nums[0]，第一个接了。

class Solution {
public:
	int massage(vector<int>& nums) 
	{
		int len = nums.size();
		if (len == 0 || len == 1)
			return len == 0 ? 0 : nums[0];
		int (*dp)[2] = new int[len][2];
		//初始值
		dp[0][0] = 0;//第一个客户不接
		dp[0][1] = nums[0];//第一个客户接
		for (int i = 1; i < len; i++)
		{
			//如果第i个客户不接，那么前面i-1位客户有两种选择:
			//1.第i-1位客户未接
			//2.第i-1位客户接了
			//既然第i位客户没有接，那么当前最大预约总时长由第i-1位客户的接与否的两种不同选择决定
			//我们要做的就是从前面两种选择中选择出预约时间最长的一种
			dp[i][0]=max(dp[i-1][0],dp[i-1][1]);

			//如果第i个客户接了，那么前面第i-1位客户只有一种选择:
			//1.第i-1位客户不接
			//那么当前预约总时长也只有一种选择，那就是到第i-1位时的最长预约时长加上当前客户的预约时长
			dp[i][1] = dp[i - 1][0] + nums[i];
		}
		//最终我们要计算的是最长预约时长:即当前所有客户都过了一遍后，我们要返回计算完最后一个客户时的dp[i-1]
		//但是我们要知道最后一位客户也存在两种状态：
		//1.被接  2.不被接
		//因此我们最终返回的应该是这两种状态中的最大值
		return max(dp[len - 1][0], dp[len-1][1]);
	}
};

动态规划的优化：

• 上面定义了一个二维数组，但每次计算的时候都只是用二维数组的前一对值，在往前面的就永远使用不到了，这样就会造成巨大的空间浪费，所以我们可以定义两个变量来解决，来看下代码

class Solution {
public:
	int massage(vector<int>& nums) 
	{
		int len = nums.size();
		if (len == 0 || len == 1)
			return len == 0 ? 0 : nums[0];
		//初始值:
		int dp0 = 0;//第一个客户没接,预约总时长为0
		int dp1 = nums[0];//第一个客户接了,预约总时长为第一个客户的预约时长
		//注意:这里第一个客户已经被计算过了，循环应该从第二个客户开始
		for (int i = 1; i < len; i++)
		{
			//同样：因为当前客户不接，计算总时长时不需要加上当前客户的预约时长
			//而计算到当前客户为止的服务总时长需要加上前面i-1位客户的服务总时长
			//又因为前面i-1位客户的服务总时长存在两种状态:没接   接了 
			//因此计算当前客户服务最长时长需要去前面两者状态的最大值
			//注意：如果这里的不保存住i-1位客户没有接客的状态，那么在计算dp1的时候加上的就是当前第i位没有接客的状态
			int temp = dp0;//用这个来保存住i-1位客户没有接客时的服务总时长
			dp0 = max(dp0, dp1);

			//同样这里只有一种选择，即前面第i-1位客户没有接的时候的总时长加上当前客户的总时长
			//这里注意:这里的dp0应该记录的是i-1位客户没有接客时的服务总时长
			dp1 = temp + nums[i];
	   }
		return max(dp0, dp1);//最后返回最后一位客户接与没接两种状态中的最大值
	}
};

使用滚动数组进行优化：

• 在编码的时候，需要注意，只要访问到 dp 数组的时候，需要对下标 % 2，等价的写法是 & 1

class Solution {
public:
	int massage(vector<int>& nums) 
	{
		int len = nums.size();
		if (len == 0 || len == 1)
			return len == 0 ? 0 : nums[0];
		int(*dp)[2] = new int[2][2];
		dp[0][0] = 0;
		dp[0][1] = nums[0];
		for (int i = 1; i < len; i++)
		{
			dp[i%2][0]=max(dp[(i-1)%2][0],dp[(i-1)%2][1]);
			dp[i % 2][1] = dp[(i - 1) % 2][0] + nums[i];
		}
		return max(dp[(len - 1)%2][0], dp[(len - 1) % 2][1]);
	}
};

对上面滚动数组实现再优化：

class Solution {
public:
	int massage(vector<int>& nums) 
	{
		int len = nums.size();
		if (len == 0 || len == 1)
			return len == 0 ? 0 : nums[0];
		int* dp = new int[2];
		//第二位客户的最长预约时长:第一位客户和第二位客户中服务时长较大者
		dp[0] = nums[0];
		 dp[1] = max(nums[0], nums[1]);
		 for (int i = 2; i < len; i++)
			 //在选与不选中，选择一个更优解
			 //如果当前选了，那么i-1就不能选，既然i-1没选，i-1的服务总时长就等于i-2的服务总时长
			 //如果当前没选,那么当前最长服务时长就是i-1的服务时长
			 dp[i & 1] = max(dp[(i - 2) & 1] + nums[i], dp[(i - 1)&1]);
             return dp[(len-1)&1];
	}
};

总结：

• 「动态规划」告诉了我们另一种求解问题的思路。我们学习编程，习惯了自顶向下求解问题（递归），在自顶向下求解问题的过程中，发现了重复子问题，我们再加上缓存。而「动态规划」告诉我们，其实有一类问题我们可以从一个最简单的情况开始考虑，通过逐步递推，每一步都记住当前问题的答案，得到最终问题的答案，即「动态规划」告诉了我们「自底向上」思考问题的思路。
• 也就是说「动态规划」告诉我们的新的思路是：不是直接针对问题求解，由于我们找到了这个问题最开始的样子，因此后面在求解的过程中，每一步都可以参考之前的结果（在处理最优化问题的时候，叫「最优子结构」），由于之前的结果有重复计算（「重复子问题」），因此必须记录下来。
• 这种感觉不同于「记忆化递归」，「记忆化递归」是直接面对问题求解，遇到一个问题解决了以后，就记下来，随时可能面对新问题。而「动态规划」由于我们发现了这个问题「最初」的样子，因此每一步参考的以前的结果都是知道的，就像我们去考试，所有的考题我们都见过，并且已经计算出了答案一样，我们只需要参考以前做题的答案，就能得到这一题的答案，这是「状态转移」。应用「最优子结构」是同一回事，即：综合以前计算的结果，直接得到当前的最优值。
• 「动态规划」的内涵和外延很丰富，不是几句话和几个问题能够理解清楚的，需要我们做一些经典的问题去慢慢理解它，和掌握「动态规划」问题思考的方向。