Exhaustive Search - 穷竭搜索

Posted 2021-05-16 大忽悠爱忽悠

题目:

• 从数组中找出任意的几个元素构成target，如果可以返回true，否则返回,false.

Exhaustive Search - 穷竭搜索

• DFS
• BFS
• 总结

---

DFS

1.递归法最初构想思路:把数组中每一个元素都作为一次根节点，进行二叉树遍历

#include<iostream>
using namespace std;
#include<vector>
class Solution
{
public:
	bool solve(vector<int>& arr,int target)
	{
		//把数组中每一个元素都作为一次根节点，进行多叉树遍历
		for (int i = 0; i < arr.size(); i++)
		{
			//如果以某个顶点出发，找到了一个正确的解，那么直接返回true
			if (dfs(arr, target, i))
				return true;
		}
		return false;
	}
	bool dfs(vector<int>& arr, int target,int beginId)
	{
          //当等于目标值那么直接返回真
		if (target == 0) return true;
		//当beginId大于数组范围的时候，返回false
		if (beginId >= arr.size()) return false;
		//这里存在选择分支:累加当前点，看是否得到目标值     不选择当前点进行累加，选择当前点下一个点进行累加
		return dfs(arr, target - arr[beginId], beginId+1)||dfs(arr,target,beginId+1);
	}
};

int main()
{
	Solution s;
	vector<int> arr = { 1,5,7,10,21 };
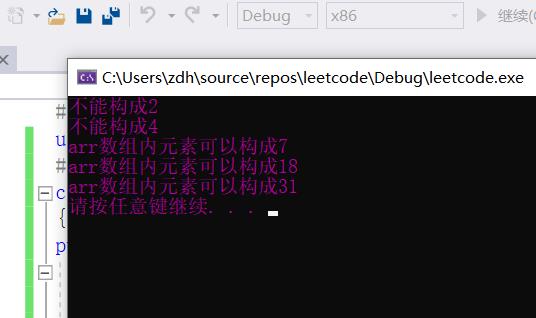
	if (s.solve(arr, 2))
		cout << "arr数组内元素可以构成2" << endl;
	else
		cout << "不能构成2" << endl;
	if (s.solve(arr, 4))
		cout << "arr数组内元素可以构成4" << endl;
	else
		cout << "不能构成4" << endl;
	if (s.solve(arr, 7))
		cout << "arr数组内元素可以构成7" << endl;
	else
		cout << "不能构成7" << endl;
	if (s.solve(arr, 18))
		cout << "arr数组内元素可以构成18" << endl;
	else
		cout << "不能构成18" << endl;
	if (s.solve(arr, 31))
		cout << "arr数组内元素可以构成31" << endl;
	else
		cout << "不能构成31" << endl;
	system("pause");
	return 0;
}

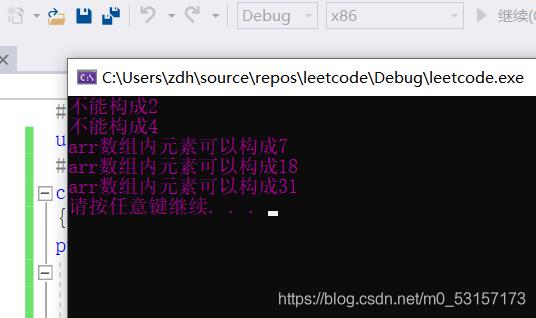
2.正确版本:把遍历的过程形象化为遍历一颗二叉树，把数组第一个元素作为多叉树的根节点

class Solution
{
public:
	bool solve(vector<int>& arr,int target,int id)
	{
		if (target == 0) return true;
		if (id >= arr.size()) return false;
	     //这里思路与上面一样,两个不同的分支选择，选还是不选
		//如果选了不成功，那么一会回来，换一个法子试试
		return solve(arr,target-arr[id],id+1)||solve(arr,target,id+1);
	}
};

总结：

• 最初的递归版本思路其实存在误区，这里题目要求的是从数组中找出任意的几个元素构成target，如果可以返回true，否则返回,false. 因此我们只需要把数组第一个元素当做根节点，进行遍历选择，注意必须是从第一个开始选择，因为我们不知道数组中哪几个元素能构成目标值，因此写法1中把剩余元素当做根节点进行遍历的做法是浪费内存和空间的(在无法构成目标值的情况下)。
• 当我们把第一个元素作为根节点进行遍历的时候，相当于就把当前遍历行为化成了一颗二叉树，这里不是多叉树，因为数组中每个元素面临两个分支选择，选择当前元素进行累加，不选择当前元素进行累加，这两种选择构成了二叉树的两个分支。

---

BFS

思路:把当前数组看做以首元素为根节点的二叉树

class Solution
{
public:
	bool solve(vector<int>& arr,int target)
	{
		queue<pair<int, int>> q; 
		q.push({ 0,target });
		q.push({ 0,target - arr[0] });
		while (!q.empty())
		{
			pair<int, int> cur = q.front();
			q.pop();
			//构成目标值，返回真
			if (cur.second == 0)
				return true;
			//当前元素，相当于二叉树的叶子节点，直接跳过，进入下一轮循环
			if (cur.first == arr.size() - 1)
				continue;
			//将一个元素选与不选的两种选择入队
			q.push({ cur.first + 1,cur.second });
			q.push({ cur.first + 1,cur.second - arr[cur.first + 1] });
		}
		return false;
	}
};

---

总结

本题做法类似于路径总和题型整理,建议没看懂这里化成二叉树思想的小伙伴，点进去看一下