leetcode 72. 编辑距离

Posted 2021-05-16 大忽悠爱忽悠

---

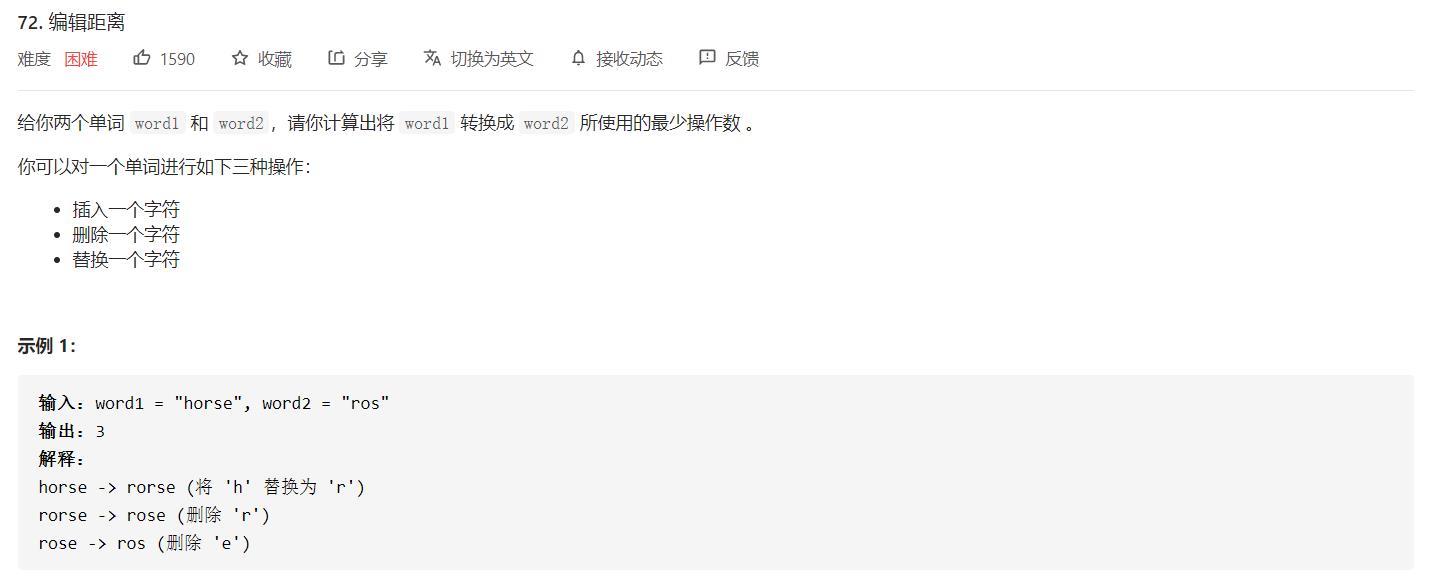
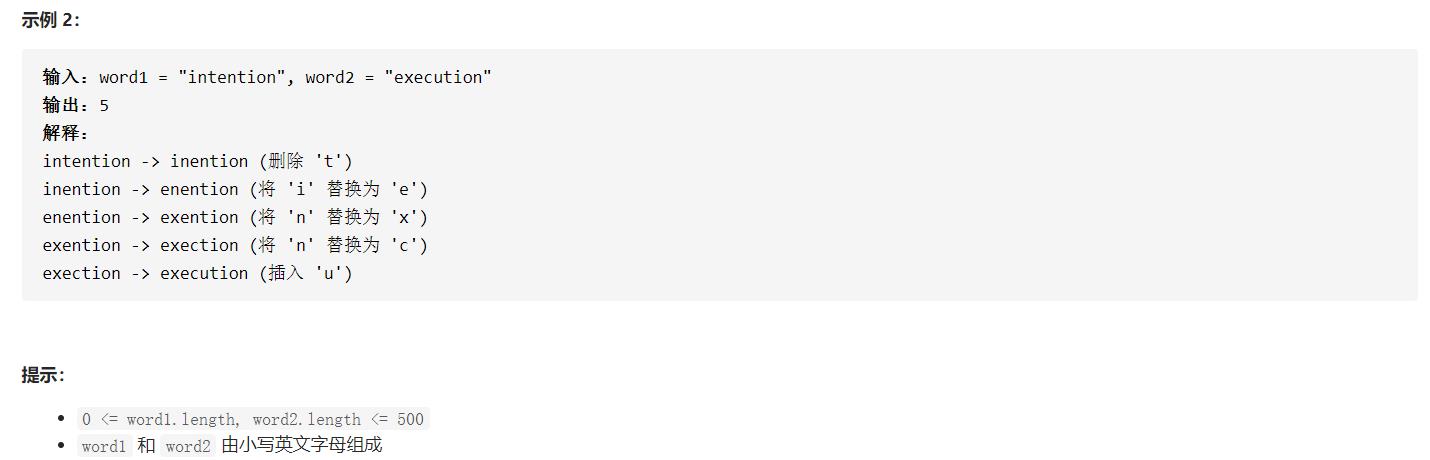
编辑距离题解集合

• 动态规划
• 动态规划的优化---优化为一维数组

---

动态规划

解题思路:

1. 定义数组元素含义

dp[i][j] 代表 word1 到 i 位置转换成 word2 到 j 位置需要最少步数

2. 找出关系数组元素间的关系式

因为我们的目标是:从规模小的，通过一些操作，推导出规模大的。对于这道题,我们可以对word1进行三种操作:
插入一个字符
删除一个字符
替换一个字符
由于我们是要让操作的次数最小，所以我们要寻找最佳操作。那么有如下关系式:
(一)、当word1[i]==word2[j]时,由于遍历到了i和j,说明word1的0~ i-1和word2的0~ j-1的匹配结果已经生成,
由于当前两个字符相同,因此无需做任何操作,dp[i][j]=dp[i-1][j-1]
(二)、当word1[i]!=word2[j]时,可以进行的操作有3个:
① 替换操作:可能word1的0~ i-1位置与word2的0~j-1位置的字符都相同,
只是当前位置的字符不匹配,进行替换操作后两者变得相同,
所以此时dp[i][j]=dp[i-1][j-1]+1(这个加1代表执行替换操作)
②删除操作:若此时word1的0~ i-1位置与word2的0~j位置已经匹配了,
此时多出了word1的i位置字符,应把它删除掉,才能使此时word1的0~i(这个i是执行了删除操作后新的i)
和word2的0~j位置匹配,因此此时dp[i][j]=dp[i-1][j]+1(这个加1代表执行删除操作)
③插入操作:若此时word1的0~ i位置只是和word2的0~j-1位置匹配,
此时只需要在原来的i位置后面插入一个和word2的j位置相同的字符使得
此时的word1的0~ i(这个i是执行了插入操作后新的i)和word2的0~j匹配得上,
所以此时dp[i][j]=dp[i][j-1]+1(这个加1代表执行插入操作)
④由于题目所要求的是要最少的操作数:所以当word1[i] != word2[j] 时,
需要在这三个操作中选取一个最小的值赋格当前的dp[i][j]
(三)总结:状态方程为:
if(word1[i] == word2[j]):
dp[i][j] = dp[i-1][j-1]
else:
min(dp[i-1][j-1],dp[i-1][j],dp[i][j-1])+1

3. 找出初始值

显然，当dp[i][j]中，如果i或者j有一个为0，那么还能使用关系式吗?
显然不能，因为i-1或者j-1为负数，所有我们的初始值计算出所有的dp[0][0…n]和dp[0…n][0]。
这个还是非常容易计算的，因为当有一个字符串的长度为0时，转化为另外一个字符串，那么就只需要一直进行插入或者删除操作即可。

class Solution {
public:
	int minDistance(string word1, string word2)
	{
		vector<vector<int>> dp(word1.size() + 1, vector<int>(word2.size() + 1));
		for (int i = 0; i < dp.size(); i++)
			dp[i][0] = i;
		for (int j = 0; j < dp[0].size(); j++)
			dp[0][j] = j;
		for (int i = 1; i < dp.size(); ++i)
		{
			for (int j = 1; j < dp[0].size(); ++j)
			{
				//这里i-1和j-1表示从第一个字符开始进行比较,因为字符串里面的第一个字符下标为0
				if (word1[i - 1] == word2[j - 1])
					//这里dp里面的i和j表示从word1开始的第i个字符，和从word2开始的第j个字符
					//如果比较的是第一个字符，那么dp里面的i和j都为1,
					dp[i][j] = dp[i - 1][j - 1];
				else
					dp[i][j] = min(dp[i - 1][j - 1], min(dp[i - 1][j], dp[i][j - 1])) + 1;
			}
		}
		return dp.back().back();
	}
};

动态规划的优化—优化为一维数组

计算第i行的值，我们只需要用到第i-1行的值，那么就可以采用一维dp来处理。

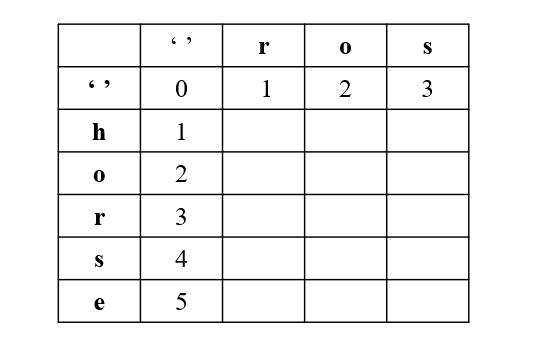
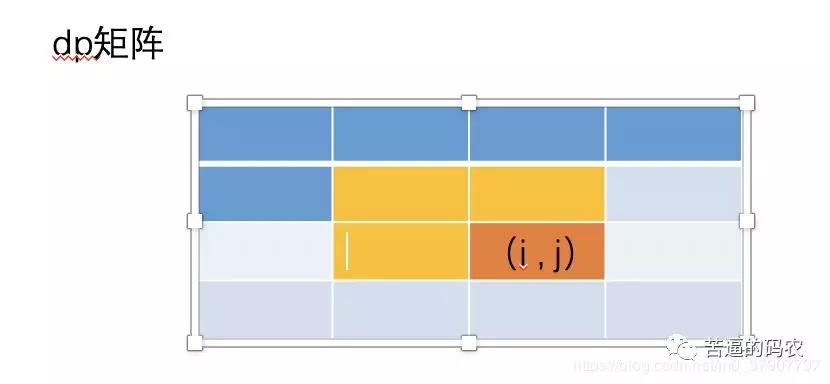
由上图可以看出，计算dp[i][j]需要用到三个地方的值，分别为(i-1,j),(i,j-1)和(i-1,j-1)，如果把当前二维数组简化为一维的化，我们需要利用到dp[i-1]未更新前的值，dp[i-1]更新后的值和dp[i]未更新前的值。
其中dp[i-1]未更新前的值会被dp[i-1]更新后的值覆盖掉，因此我们需要用一个pre变量保存dp[i-1]未更新前的值
那么这里dp[i-1]未更新前的值对应(i-1,j-1)
dp[i-1]更新后的值对应(i-1,j)
dp[i]未更新前的值对应(i,j-1)

dp[i]=min(dp[i-1],pre,dp[i])+1;

下面看代码:

class Solution {
public:
	int minDistance(string word1, string word2)
	{
		vector<int> dp(word2.size()+1);
		//word2长度作为行的长度
		//word1长度作为列的长度

		//计算第一行的长度,我们这里是一行行求出来的，第二行依赖第一行求出
		for (int i = 0; i <= word2.size(); ++i)
			dp[i]=i;
		//外层循环每执行一次，就求解新的一行，因为第一行已经求解出来了，所以从第二行开始求解
		for (int i = 1; i <= word1.size(); ++i)
		{
			//内存循环从当前行第二个元素开始求解
			//注意我们保存第一行的第一个元素，相当于保存(i-1,j-1)
			int temp = dp[0];
			//更新dp[0]为当前行第一个元素的值
			dp[0] = i;
			for (int j = 1; j <= word2.size(); ++j)
			{
				int pre = temp;//保存dp(i-1,j-1)
				temp = dp[j];
				//字符串字符下标从0开始
				if (word1[i - 1] == word2[j - 1])
					dp[j] = pre;
				else//dp[j-1]对应dp(i-1,j)  pre对应dp(i-1,j-1)  dp[j]对应dp(i,j-1)
					dp[j] = min(dp[j - 1], min(pre, dp[j])) + 1;
			}
		}
		return dp.back();
	}
};