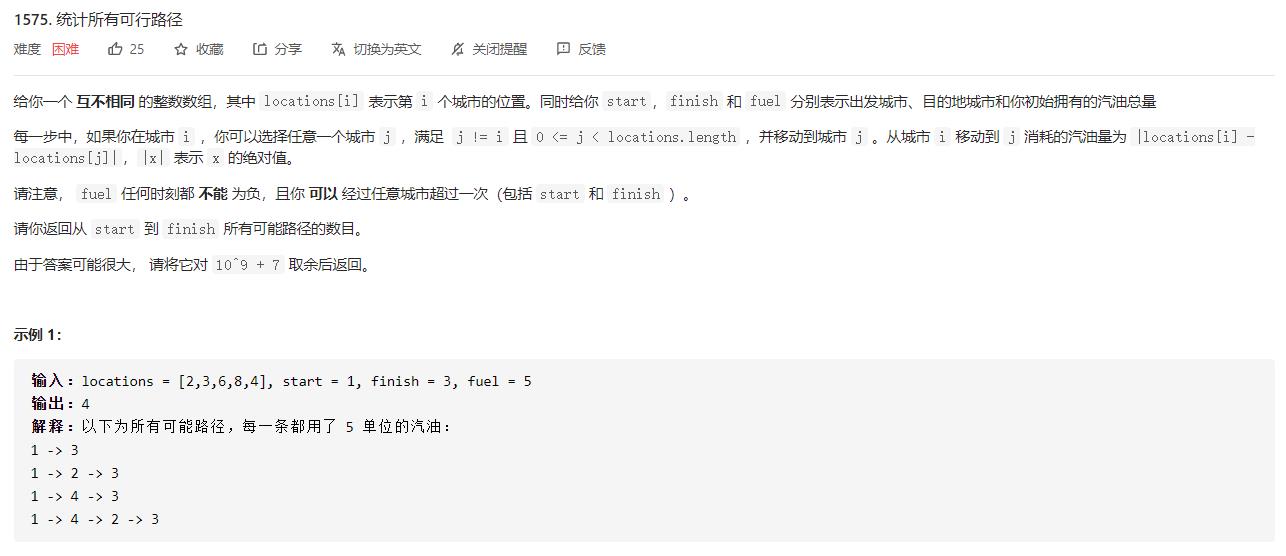
leetcode 1575. 统计所有可行路径

Posted 2021-05-16 大忽悠爱忽悠

统计所有可行路径解法目录

• 记忆化搜索
• 动态规划
• 总结

记忆化搜索

我们知道，如果要实现 DFS 的话，通常有以下几个步骤：

1. 设计好递归函数的「入参」和「出参」
2. 设置好递归函数的出口（Base Case）
3. 编写「最小单元」处理逻辑
   对于大多数的 DFS 来说，第 1 步和第 3 步都很好实现，而找 Base Case 通常是三部曲中最难的。

---

以本题为例，我们来剖析一下该如何找 Base Case。

• 首先要明确，所谓的找 Base Case，其实是在确定什么样的情况下，算一次有效/无效。
• 对于本题，找 Base Case 其实就是在确定：什么样的情况下，算是 0 条路径；什么样的情况下，算是 1 条路径。
• 然后再在 DFS 过程中，不断的累加有效情况（算作路径数量为 1）的个数作为答案。
• 这是 DFS 的本质，也是找 Base Case 的思考过程。
• 回到本题，对于 有效情况 的确立，十分简单直接，如果我们当前所在的位置 i就是目的地 finish的话，那就算成是一条有效路径，我们可以对路径数量进行 +1。

那么如何确立 无效情况 呢？

• 一个直观的感觉是当油量消耗完，所在位置又不在 finish，那么就算走到头了，算是一次「无效情况」，可以终止递归。
• 逻辑上这没有错，但是存在油量始终无法为零的情况。
• 考虑以下样例数据：

locations = [0,2,2,2], 
start = 0, 
finish = 3, 
fuel = 1

• 我们当前位置在 0，想要到达 3，但是油量为 1，无法移动到任何位置。
• 也就是如果我们只考虑 fuel = 0作为 Base Case 的话，递归可能无法终止。
• 因此还要增加一个限制条件：油量不为 0，但无法再移动到任何位置，也算是一次「无效情况」，可以终止递归。
• 到这里，我们已经走完「DFS 的三部曲」了，然后由于本题的数据范围超过了 30，我们需要为 DFS 添加「记忆化搜索」。
• 缓存器的设计也十分简单，使用二维数组 cache[][]进行记录即可。
• 我们用 cache[i][fuel]代表从位置 i出发，当前剩余的油量为 fuel 的前提下，到达目标位置的「路径数量」。
• 之所以能采取「缓存中间结果」这样的做法，是因为在 i和 fuel 确定的情况下，其到达目的地的路径数量是唯一确定的。

---

代码：

 class Solution {
	 // 缓存器：用于记录「特定状态」下的结果
	 // cache[i][fuel] 代表从位置 i 出发，当前剩余的油量为 fuel 的前提下，到达目标位置的「路径数量」
	 vector<vector<int>>  cache;
	 static constexpr int mod = 1000000007;
 public:
     int countRoutes(vector<int>& locations, int start, int finish, int fuel) 
	 {
		 int n = locations.size();
		 // 初始化缓存器
		// 之所以要初始化为 -1
		// 是为了区分「某个状态下路径数量为 0」和「某个状态尚未没计算过」两种情况
		 cache.resize(n,vector<int>(fuel+1,-1));
		 return dfs(locations, start, finish, fuel);
     }
     //ls：入参 locations      u 当前所在位置（ls 的下标）
	 //end 目标哦位置（ls 的下标）  fuel 剩余油量
	 //返回值: 在位置 u 出发，油量为 fuel 的前提下，到达 end 的「路径数量」
	 int dfs(vector<int>& ls, int u, int end, int fuel)
	 {
		 // 如果缓存器中已经有答案，直接返回
		 if (cache[u][fuel] != -1)
			 return cache[u][fuel];

		 int n = ls.size();
		 //base case 1：如果油量为 0，且不在目标位置
        // 将结果 0 写入缓存器并返回
		 if (fuel == 0 &&u != end)
		 {
			 cache[u][fuel] = 0;
			 return 0;
		 }

		 // base case 2：油量不为 0，且无法到达任何位置
		// 将结果 0 写入缓存器并返回
        //当前油量不为0，但是如果当前起点到终点最短距离所需要的油量都不够，那么直接返回0
		 int minNeed = abs(ls[u] - ls[end]);
		 if (minNeed>fuel&&fuel!=0)
		 {
			 cache[u][fuel] = 0;
			 return 0;
		 }

		 // 计算油量为 fuel，从位置 u 到 end 的路径数量
		// 由于每个点都可以经过多次，如果 u = end，那么本身就算一条路径
		 int sum = (u == end) ? 1 : 0;
		 for (int i = 0; i < n; i++)
		 {
			 if (i != u)
			 {
				 int need = abs(ls[i] - ls[u]);
				 if (fuel >=need)
				 {
					 sum += dfs(ls, i, end, fuel-need);
					 sum %= mod;
				 }
			 }
		 }
		 cache[u][fuel] = sum;
		 return sum;
	 }
 };

---

动态规划

• 将「记忆化搜索」改成「动态规划」。
• 使用这种技巧，你将不需要去猜「状态定义」和根据「状态定义」推导「状态转移方程」。
• 我们重点关注下我们的 DFS 方法签名设计：

int dfs(int[] ls, int u, int end, int fuel) {}

• 其中，ls 参数和 end参数分别代表源输入的 locations 和 finish，在整个DFS 过程都不会变化，属于不变参数。
• 而 u参数和 fuel 参数则是代表了 DFS 过程中的当前位置和当前油量，属于变化参数。
• 因此我们可以定一个 f[][]二维数组，来分别表示两个可变参数。
• 第一维代表当前位置（对应 locations 数组的下标），第二维代表当前剩余油量。
• 二维数组中存储的就是我们的 DFS 方法的返回值（路径数量）。
• 同时结合题意，不难得知维度的取值范围：
• 第一维的取值范围为 [0, locations.length)
• 第二维的取值范围为 [0, fuel]
• 做完这一步的”翻译“工作，我们就得到了「动态规划」的「状态定义」了。
• f[i][j]代表从位置 i出发，当前剩余油量为 j 的前提下，到达目的地的路径数量。
• 不知道你是否发现，这个「状态定义」和我们「记忆化搜索」中的缓存器的定义是一致的。
• 接下来我们要从 DFS 中”翻译“出「状态转移方程」。
• 所谓的「状态转移方程」其实就是指如何从一个状态转移到另外一个状态。
• 而我们的 DFS 主逻辑就是完成这个转移的。
• DFS 中的主逻辑很简单：枚举所有的位置，看从当前位置 u 出发，可以到达的位置有哪些。
• 于是我们很容易就可以得出状态转移方程：
• f[i][fuel]=f[i][fuel]+f[k][fuel-need]
• k代表计算位置 i 油量 fuel 的状态时枚举的「下一位置」，need 代表从 i 到达 k 需要的油量。
• 从状态转移方程可以发现，在计算 f[i][fuel]的时候依赖于f[k][fuel-need]。
• 其中 i 和 k 并无严格的大小关系，而 fuel和fuel−need 具有严格的大小关系（fuel≥fuel−need）。
• 因此我们需要先从小到大枚举油量这一维。

代码：

 class Solution {
 public:
     int countRoutes(vector<int>& locations, int start, int finish, int fuel) 
	 {
		 int n = locations.size();
		 // f[i][j] 代表从位置 i 出发，当前油量为 j 时，到达目的地的路径数
		 vector<vector<int>>  f(n, vector<int>(fuel + 1,0));
		 static constexpr int mod = 1000000007;
		 // 对于本身位置就在目的地的状态，路径数为 1
		 for (int i = 0; i <= fuel; i++) f[finish][i] = 1;

	  // 从状态转移方程可以发现 f[i][fuel]=f[i][fuel]+f[k][fuel-need]
	  // 在计算 f[i][fuel] 的时候依赖于 f[k][fuel-need]
	  // 其中 i 和 k 并无严格的大小关系
	  // 而 fuel 和 fuel-need 具有严格大小关系：fuel >= fuel-need
	  // 因此需要先从小到大枚举油量
		 for (int cur = 0; cur <= fuel; cur++)//cur表示油量大小
		 {
			 //这里暴力思路:枚举每一个位置作为起点，计算当前起点到终点的所有路径数目
			 for (int i = 0; i < n; i++)//当前位置起点
			 {
				 for (int j = 0; j < n; j++)//当前起点要到达的下一位置
				 {
					 if (i != j)//当前位置不能呆在原地不动
					 {
						 int need = abs(locations[i] - locations[j]);//当前位置到下一个位置消耗的油量
						 if (cur >= need)//当前油量能满足到达下一个位置
						 {
							 //f[i][cur] 代表从位置 i 出发，当前剩余油量为 cur 的前提下，到达目的地的路径数量。
							 //j是当前位置的下一个位置，当前位置到达目的地的路径数量应该是下一个位置到达目的地的数量加上自身到达目的地的数量
							 f[i][cur] += f[j][cur - need];
							 f[i][cur] %= mod;
						 }
					 }
				 }
			 }
         }
		 return f[start][fuel];
     }

 };

• 没有理解下面这行代码，没关系，来看图

 f[i][cur] += f[j][cur - need];

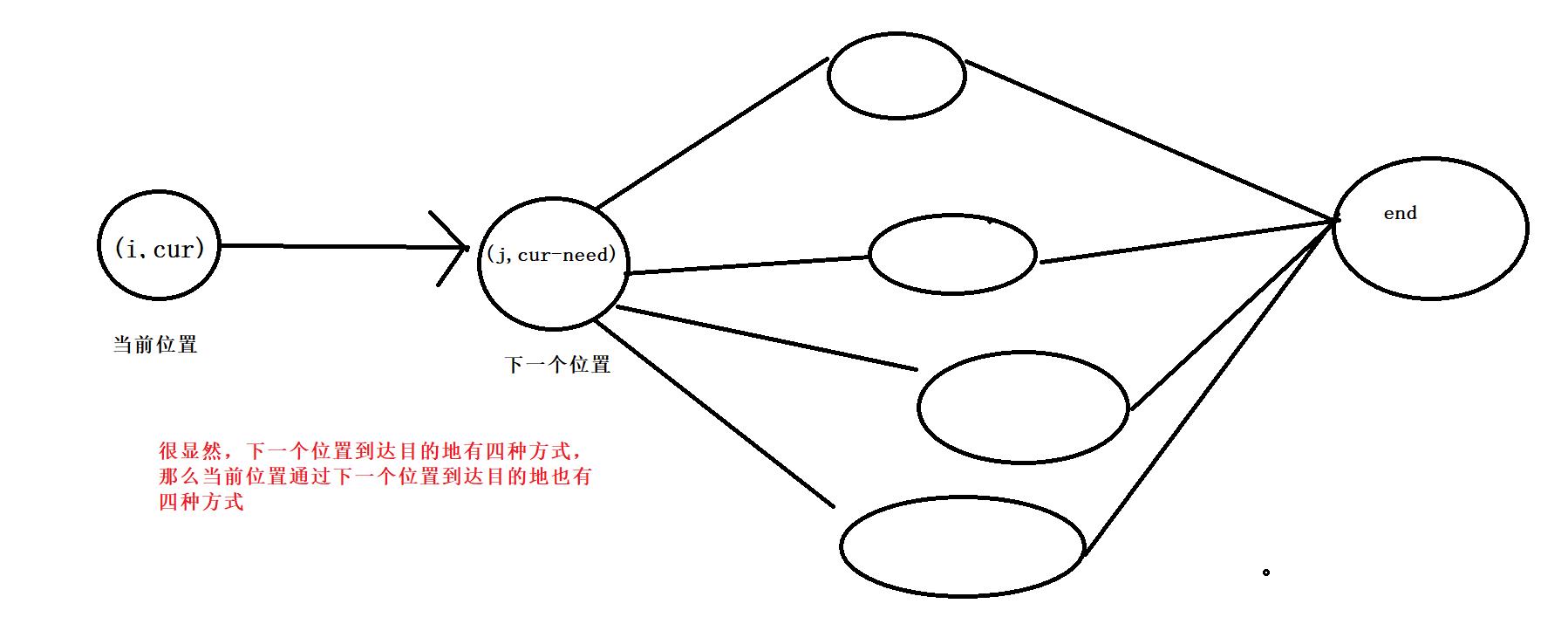
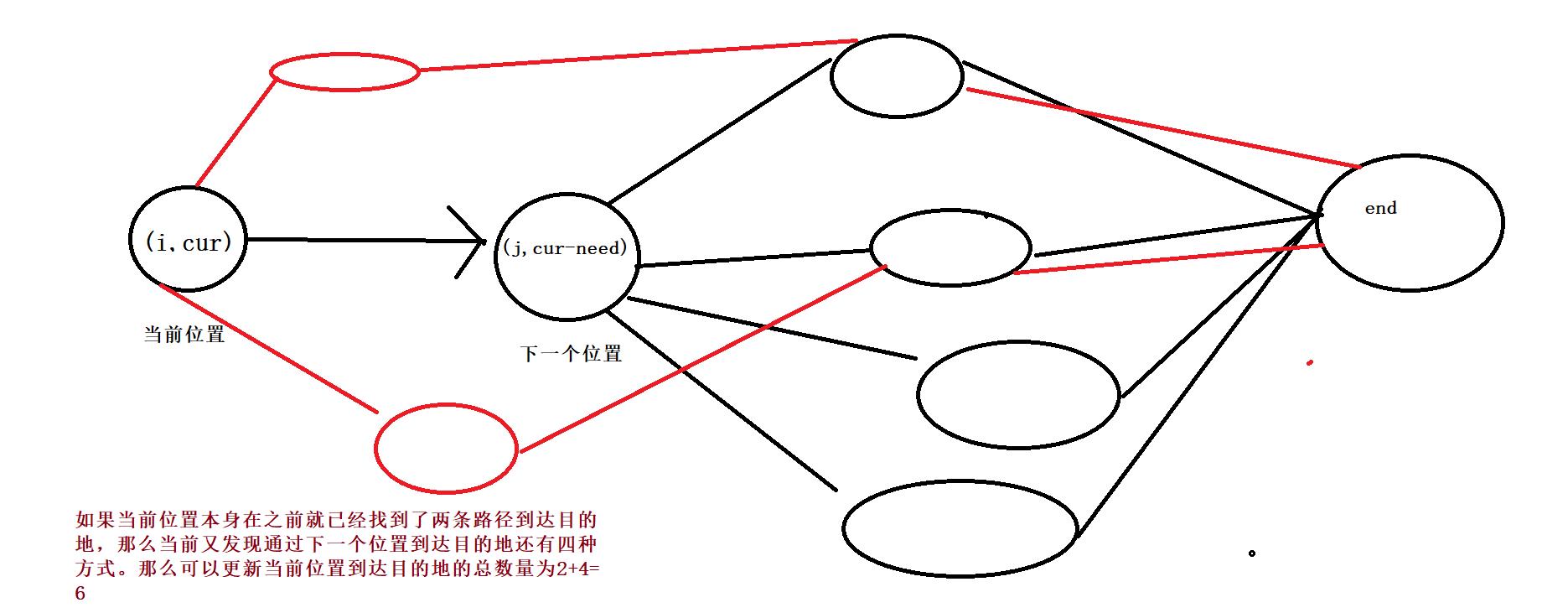
• 同理，如果之前已经计算出了当前位置到达目的地有f[i][cur]种方式，现在又发现下一位置到达目的地还有dp[j][cur-need]种方式，那么更新当前位置到达目的地的总路径数量为f[i][cur] += f[j][cur - need];
• 时间复杂度：最坏情况下共有 n * fuel 个状态需要计算（填满整个 cache数组）。每计算一个状态需要遍历一次 locations 数组，复杂度为 O(n)。整体复杂度为 O(n^2 *fuel)
• 空间复杂度：O(n^2 * fuel)
• 至此，我们只利用 DFS 的方法签名与主逻辑，就写出了「动态规划」解法。

我再帮你来总结一下这个过程：

• 从 DFS 方法签名出发。分析哪些入参是可变的，将其作为 DP 数组的维度；将返回值作为 DP 数组的存储值。
• 从 DFS 的主逻辑可以抽象中单个状态的计算方法。

其中第一点对应了「动态规划」的「状态定义」，第二点对应了「动态规划」的「状态方程转移」。

我希望你借此好好体会一下「记忆化搜索」与「动态规划」的联系。

---

总结

今天，我与你分享了如何直接将「记忆化搜索」改成「动态规划」，而无需关心具体的「状态定义」和「状态转移方程」。

到目前为止，我们已经掌握了两种求解「动态规划」问题的方法：

1. 根据经验猜一个「状态定义」，然后根据「状态定义」去推导一个「状态转移方程」。

2. 先写一个「记忆化搜索」解法，再将「记忆化搜索」改写成「动态规划」。

能够去猜「状态定义」或者使用「记忆化搜索」求解，都有一个大前提：问题本身具有无后效性。

由于「动态规划」的状态定义猜测，是一门很讲求经验的技能。

因此对于那些你接触过的模型，我建议你使用第一种方式；

如果遇到一道你从来没接触过的题目时，我建议你先想想「记忆化搜索」该如何实现，然后反推出「动态规划」。

这里说的想想「记忆化搜索」该如何实现，不需要真正动手实现一个「记忆化搜索」解法，而只需要想清楚，如果使用「记忆化搜索」的话，我的 DFS 函数签名如何设计即可。

当搞清楚「记忆化搜索」的函数签名设计之后，「状态定义」部分基本就已经出来了，之后的「状态转移方程」就还是一样的分析方法。

当然，如果你觉得「记忆化搜索」更好实现的话，大可直接使用「记忆化搜索」求解，不一定需要将其转化为「动态规划」。

因为由「记忆化搜索」直接转过来的「动态规划」，两者复杂度是一样的。而且通常「记忆化搜索」的实现难度通常要低很多。